在別人眼里輕而易舉的的事情落在自己身上可能比登天還要難！！
0-1背包問題：給定n中物品和一個背包。物品i的重量是wi，價值為vi，背包的容量為c。問如何選擇裝入背包中的武平，使得裝入背包中的物品價值最大？
書上有一行行的算式，證明最優子結構性質和構造遞歸關系。我沒怎么看明白最優子結構，但是我能看懂遞歸關系式！！我記得當時老師叫我們的時候我自己想了好幾天才想明白這個遞歸式，但是始終覺得有點虛，借此我再寫一下！
設數組m(i,j)代表背包容量為j，可選物品為i，i+1，..n時的最優解（這里的最優解指的是選擇方案，并非正真的最優值），顯然m(1,c)是0-1背包問題的解（
這里是書上的錯誤，應該是m[1]中的最大值！！我后來才發現的。。）。這種定義雖然比較拗口，但是還是可以接受的，其實我們也可以這么定義m[i][j],代表背包容量為j，當前選擇物品為a[i]時的最優解，顯然m數組中第n行的最大值是0-1背包問題的解！！
第一種定義的遞歸式如下：
0 1
m[i][j]=max{m[i+1][j],m[i+1][j-wi]+vi} j>=wi; m[i][j]=m(i+1,j) 0<=j<wi
第二種定義的遞歸式如下：
0 1 m[i][j]=max{m[i-1][j],m[i-1][j-wi]+vi} j>=wi; m[i][j]=m(i-1,j) 0<=j<wi
代碼如下：
#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;
int max(int x,int y)
{
if(x>y)
return x;
return y;
}
int min(int x,int y)
{
if(x>y)
return y;
return x;
}
template <class Type>
void Knapsack(Type *v,int *w,int c,int n,Type m[][20])//構造m，最優取舍方案函數！！
{
int i,j;
int jMax=min(w[n]-1,c);
for(j=0;j<=jMax;j++)
m[n][j]=0;
for(j=w[n];j<=c;j++)
m[n][j]=v[n];
for(i=n-1;i>=1;i--)
{
jMax=min(w[i]-1,c);
for(j=0;j<jMax;j++)
m[i][j]=m[i+1][j];
for(j=w[i];j<=c;j++)
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
/**//* m[1][c]=m[2][c];
if(c>=w[1])
m[1][c]=max(m[1][c],m[2][c-w[1]]+v[1]);*///這里是書上的一個錯誤，并不是m[1][c]就是0-1背包問題的解，事實上m[1]上的所有解都有可能！！
//所以還是應該把m[1]上的所有最優構造都算出來，然后去最大值
}
template <class Type> //構造x數組函數
void Traceback(Type m[][20],int *w,int c,int n,int x[])
{
int i;
for(i=1;i<n;i++)
{
if(m[i][c]==m[i+1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
}
x[n]=(m[n][c])?1:0;
}
int main()
{
int w[10],v[10],x[10],m[20][20],c,n,max,c0;
int i,j;
while(scanf("%d",&n)!=EOF)
{
max=0;
memset(m,0,sizeof(m));
for(i=1;i<=n;i++)
{
scanf("%d %d",&w[i],&v[i]);
}
scanf("%d",&c);
Knapsack(v,w,c,n,m); //構造最優取舍方案
for(i=1;i<=c;i++)
{
if(m[1][i]>max)
{
max=m[1][i];
c0=i;
}
}
Traceback(m,w,c0,n,x); //構造x數組
printf("最優矩陣如下：\n");
for(i=1;i<=n;i++)
{
for(j=0;j<=c;j++)
printf("%d ",m[i][j]);
printf("\n");
}
printf("方案如下：\n");
for(i=1;i<=n;i++)
printf("%d ",x[i]);
printf("\n");
}
return 0;
}運行結果如下：
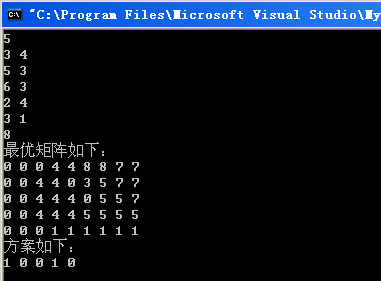
第二種遞歸思路下的代碼和運行過程我就不寫，就初始化和遞歸次序不同！！
我一個同學經常跟我說，以后自己有孩子，一個賺了1000給我花100，一個賺了10000給我花200，我還是跟著賺1000的吧！！其實問題不在別人，而在自己，努力就成！！！我受益匪淺。。。
posted on 2010-09-11 16:32
jince 閱讀(1847)
評論(0) 編輯 收藏 引用 所屬分類:
算法設計與分析