TOJ有道題,大意是有N個(gè)位置,每個(gè)位置有若干瓶子,Mike很淘氣,他每次會(huì)增加或減少位置i的瓶子數(shù),然后有M次詢問,求位置A到B的瓶子數(shù)的和。最開始,我一直用最直觀的做法,但是由于是O(n)的復(fù)雜度,所以一直超時(shí)。今天看了BIT的相關(guān)東西,才發(fā)現(xiàn)那個(gè)題其實(shí)是典型的BIT題目,而且是最基礎(chǔ)的,但是就和RMQ問題一樣,高效的算法背后深刻的數(shù)學(xué)理論還是不能很透徹的理解,這個(gè)只有靠以后熟練的慢慢來了:D
先來看一下樹狀數(shù)組的概念:樹狀數(shù)組是一種靜態(tài)樹狀數(shù)據(jù)結(jié)構(gòu),它的首要作用是維護(hù)前綴和,即改變數(shù)組中某一元素a[i]的值,若要詢問前N項(xiàng)的和,樹狀數(shù)組便可完美解決。時(shí)間復(fù)雜度O(logn)。
先來直觀看一下樹狀數(shù)組的結(jié)構(gòu)(圖片來自http://fqq11679.blog.hexun.com/21722866_d.html#)
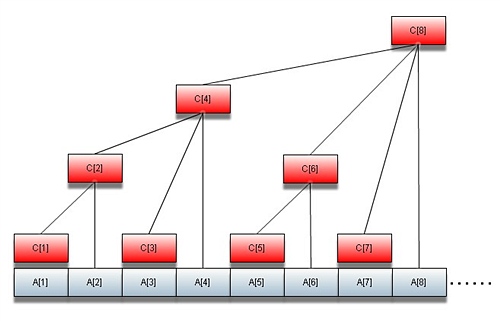
在上圖中,紅色的數(shù)組c[]便是樹狀數(shù)組。改變數(shù)組a的某一個(gè)元素i,則需要相應(yīng)的改變數(shù)組c,若要詢問前N項(xiàng)和,只需累加相應(yīng)的c,而這當(dāng)中一個(gè)核心的問題便是相應(yīng)的數(shù)組c的下標(biāo)問題。可以用位操作lowbit解決。c[i]=a[i-2^k+1]到a[i]的和,k是指i用二進(jìn)制表示時(shí)末位0的個(gè)數(shù),即將i表示成冪方和后最小的指數(shù)。利用位運(yùn)算,我們可以得知2^k=i&(i^(i-1));
相應(yīng)的代碼為:
1 int lowbit(int n)
2 {
3 return n&(n^(n-1));
4 }
這樣,當(dāng)a[i]改變時(shí),我們只需從c[i]開始一直向上回溯,改變路上相應(yīng)的數(shù)組c的值,若要求前N項(xiàng)和,只需求N以前所有最大子樹c[]的和。然后我們來看相應(yīng)下標(biāo)的操作:
修改a[i],則修改一路的父節(jié)點(diǎn)c[p], p=i-bit(i);
若要前i項(xiàng)求和,只需一路找子節(jié)點(diǎn)c[p], p=i-lowbit(i);
求前N項(xiàng)和:
1 int sum(int n)
2 {
3 int total=0;
4 while(n>0){
5 total+=c[n];
6 n-=lowbit(n);
7 }
8 return total;
9 }
TOJ 3505 Naughty mike
Code:
1 /*TOJ 3505 Naughty mike*/
2 #include<stdio.h> //注意在使用樹狀數(shù)組時(shí)下標(biāo)一定不能從0開始
3 #include<string.h>
4 #define M 100002
5 int a[M],n;
6 int c[M];
7 int lowbit(int t) //關(guān)鍵的位操作確定數(shù)組下標(biāo)
8 {
9 return t&(t^(t-1));
10 }
11 int sum(int end) //求前end項(xiàng)和的函數(shù),通過不斷累加最大子樹得到
12 {
13 int i;
14 int total=0;
15 while(end>0){
16 total+=c[end];
17 end-=lowbit(end);
18 }
19 return total;
20 }
21 void modify(int t,int key) //對數(shù)組某一項(xiàng)進(jìn)行修改時(shí),只需沿該項(xiàng)一直向上回溯修改相應(yīng)的數(shù)組c
22 {
23 while(t<=n){
24 c[t]+=key;
25 t+=lowbit(t);
26 }
27 }
28 int main()
29 {
30 int i,j,k,m,cas;
31 char e[50];
32 scanf("%d",&cas);
33 while(cas--){
34 scanf("%d",&n);
35 memset(c,0,sizeof(c));
36 for(i=1;i<=n;i++){
37 scanf("%d",&a[i]);
38 modify(i,a[i]);
39 }
40 scanf("%d",&m);
41 while(m--){
42 scanf("%s%d%d",e,&i,&j);
43 if(e[0]=='A'){
44 modify(i,j);
45 a[i]+=j;
46 }
47 else if(e[0]=='D'){
48 if(j>=a[i]) j=(-1)*a[i]; //由于可能刪除的比現(xiàn)有的還多,需要分開考慮
49 else j*=(-1);
50 modify(i,j);
51 a[i]+=j;
52 }
53 else
54 printf("%d\n",sum(j)-sum(i-1)); //區(qū)間[i,j]的和
55 }
56 }
57 }
58