1. OpenGL 渲染管線

OpenGL渲染管線分為兩大部分，模型觀測變換(ModelView Transformation)和投影變換(Projection Transformation)。做個(gè)比喻，計(jì)算機(jī)圖形開發(fā)就像我們照相一樣，目的就是把真實(shí)的場景在一張照相紙上表現(xiàn)出來。那么觀測變換的過程就像是我們擺設(shè)相機(jī)的位置，選擇好要照的物體，擺好物體的造型。而投影變換就像相機(jī)把真實(shí)的三維場景顯示在相紙上一樣。下面就分別詳細(xì)的講一下這兩個(gè)過程。

1.1模型觀測變換

讓我們先來弄清楚OpenGL中的渲染管線。管線是一個(gè)抽象的概念，之所以稱之為管線是因?yàn)轱@卡在處理數(shù)據(jù)的時(shí)候是按照一個(gè)固定的順序來的，而且嚴(yán)格按照這個(gè)順序。就像水從一根管子的一端流到另一端，這個(gè)順序是不能打破的。先來看看下面的圖1：

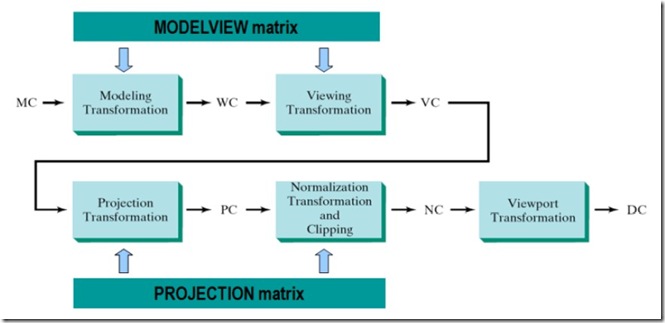                     圖1 OPENGL渲染管線                                 

圖中顯示了OpenGL圖形管線的主要部分，也是我們在進(jìn)行圖形編程的時(shí)候常常要用到的部分。一個(gè)頂點(diǎn)數(shù)據(jù)從圖的左上角(MC)進(jìn)入管線，最后從圖的右下角(DC)輸出。MC是Model Coordinate的簡寫，表示模型坐標(biāo)。DC是Device Coordinate的簡寫，表示設(shè)備坐標(biāo)。 當(dāng)然DC有很多了，什么顯示器，打印機(jī)等等。這里DC我們就理解成常說的屏幕坐標(biāo)好了。MC當(dāng)然就是3D坐標(biāo)了(注意：我說的3D坐標(biāo)，而不是世界坐 標(biāo))，這個(gè)3D坐標(biāo)就是模型坐標(biāo)，也說成本地坐標(biāo)(相對于世界坐標(biāo))。MC要經(jīng)過模型變換(Modeling Transformation)才變換到世界坐標(biāo)，圖2：

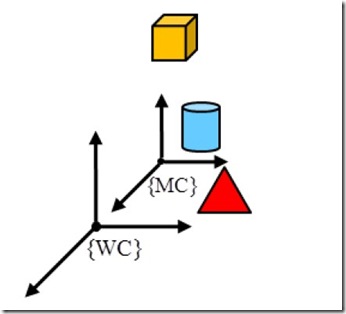圖2 世界坐標(biāo)系和模型坐標(biāo)系

變換到世界坐標(biāo)WC(World Coordinate)說簡單點(diǎn)就是如何用世界坐標(biāo)系來表示本地坐標(biāo)系中的坐標(biāo)。為了講得更清楚一些，這里舉個(gè)2D的例子。如圖3：

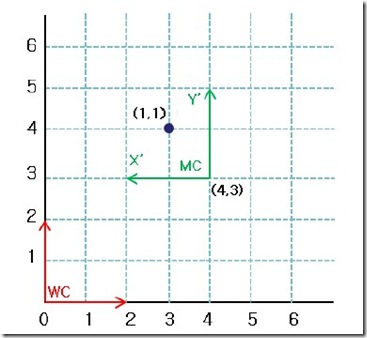圖3 世界坐標(biāo)系和模型坐標(biāo)系的計(jì)算

圖中紅色坐標(biāo)系是世界坐標(biāo)系WC，綠色的是模型坐標(biāo)系MC。現(xiàn)在有一個(gè)頂點(diǎn)，在模型坐標(biāo)系中的坐標(biāo)為(1,1)，現(xiàn)在要把這個(gè)模型坐標(biāo)轉(zhuǎn)換到世界坐標(biāo)中來表示。從圖中可以看出，點(diǎn)(1,1)在世界坐標(biāo)系中的坐標(biāo)為(3,4)，現(xiàn)在我們來通過計(jì)算得到我們希望的結(jié)果。首先我們要把模型坐標(biāo)系MC在世界坐標(biāo)系中表示出來，使用齊次坐標(biāo)(Homogeneous Coordinate )可以表示為矩陣(注意，本教程中使用的矩陣都是以列向量組成)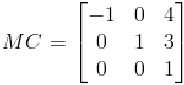： 其中，矩陣的第一列為MC中x軸在WC中的向量表示，第二列為MC中y軸WC中的向量表示，第三列為MC中的原點(diǎn)在WC中的坐標(biāo)。對齊次坐標(biāo)系不了解的同學(xué)，請先學(xué)習(xí)游戲數(shù)學(xué)方面的知識。有了這個(gè)模型變換矩陣后，用這個(gè)矩陣乘以在MC中表示的坐標(biāo)就可以得到該坐標(biāo)在世界坐標(biāo)系中的坐標(biāo)。所以該矩陣和MC中的坐標(biāo)(1,1)相乘有:

這也正是我們需要的結(jié)果。現(xiàn)在讓我們把相機(jī)坐標(biāo)也加進(jìn)去，相機(jī)坐標(biāo)也稱為觀測坐標(biāo)(View Coordinate)，如圖4和圖5。

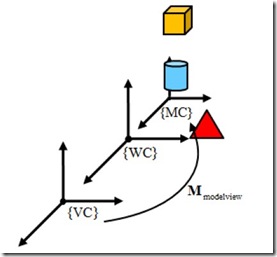圖4 ModelView變換的三個(gè)坐標(biāo)系

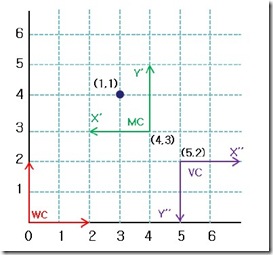圖5 ModelView變換計(jì)算

來看看MC坐標(biāo)中的點(diǎn)(1,1)如何在相機(jī)坐標(biāo)中表示。從圖5中可以直接看出MC中的點(diǎn)(1,1)在相機(jī)坐標(biāo)系VC中為(-2,-2)。和上面同樣的道理，我們可以寫出相機(jī)坐標(biāo)系VC在世界標(biāo)系WC中可以表示為：

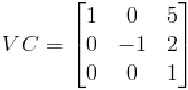那么世界坐標(biāo)系中的點(diǎn)轉(zhuǎn)換為相機(jī)坐標(biāo)系中的點(diǎn)我們就需求VC的逆矩陣：

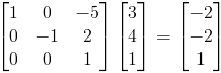
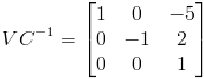那么世界坐標(biāo)系WC中的點(diǎn)(3,4)在相機(jī)坐標(biāo)系VC中坐標(biāo)為：

上面的變換過程，就是可以把模型坐標(biāo)變換為相機(jī)坐標(biāo)。在OpenGL中，當(dāng)我們申明頂點(diǎn)的時(shí)候，有時(shí)候說的是世界坐標(biāo)，這是因?yàn)槌跏蓟臅r(shí)候世界坐標(biāo)系、模型坐標(biāo)系和相機(jī)坐標(biāo)系是一樣的，重合在一起的。所以O(shè)penGL中提供了模型觀測變換，它是把模型坐標(biāo)系直接轉(zhuǎn)換為相機(jī)坐標(biāo)系，如圖4。現(xiàn)在我們已經(jīng)計(jì)算得到了VC^-1和MC，如果把VC^-1和 MC相乘，就可以得到模型坐標(biāo)在相機(jī)坐標(biāo)中的表示。為了得到模型坐標(biāo)系中的坐標(biāo)在相機(jī)坐標(biāo)系中的表示，這就是OpenGL中的ModelView變換矩 陣。這也是ModelView變換的名字的由來，它是通過了上面兩個(gè)步驟得到的。那么這里，ModelView變換矩陣M為：

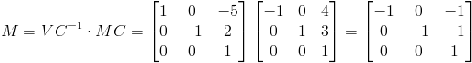現(xiàn)在只要用上面的模型觀測矩陣M乘以模型坐標(biāo)系MC中的坐標(biāo)就可以得到相機(jī)坐標(biāo)系中的坐標(biāo)了。模型觀測變換的關(guān)鍵就是要得到相機(jī)坐標(biāo)系中的坐標(biāo)，因?yàn)楣庹盏扔?jì)算都是在這個(gè)這個(gè)坐標(biāo)系中完成的。下面我們實(shí)際OpenGL程序中檢查一下。在程序中，為了計(jì)算方便，我們使用圖6中的模型。

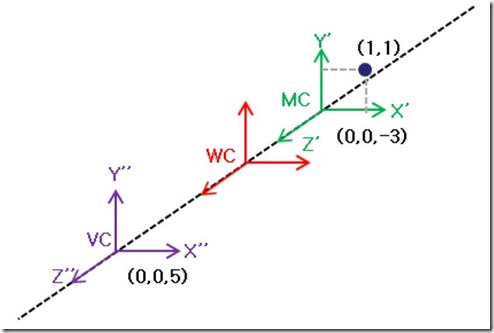圖6 ModelView變換計(jì)算模型

根據(jù)圖中的數(shù)據(jù)，我們分別可以寫出對應(yīng)MC和VC^-1，從而求得觀測變換矩陣M。

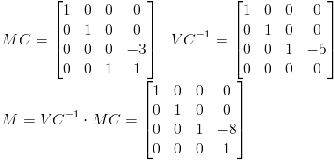現(xiàn)在程序中用glGetFloatv()這個(gè)函數(shù)來獲得當(dāng)前矩陣數(shù)據(jù)來檢查一下。

[cpp] view plaincopy
float m[16] = {0}; //用來保存當(dāng)前矩陣數(shù)據(jù)  
glMatrixMode(GL_MODELVIEW);  
glLoadIdentity();  
glGetFloatv(GL_MODELVIEW_MATRIX, m);   
//相機(jī)設(shè)置，View 變換  
gluLookAt(0.0, 0.0, 5.0,  
0.0, 0.0, 0.0,  
0.0, 1.0, 0.0);  
glGetFloatv(GL_MODELVIEW_MATRIX, m);   
//投影設(shè)置  
glMatrixMode(GL_PROJECTION);  
glLoadIdentity();  
glOrtho(-10,10,-10,10,-10,10);  
glMatrixMode(GL_MODELVIEW);   
//Modeling變換  
glTranslatef(0, 0, -3);  
glGetFloatv(GL_MODELVIEW_MATRIX, m);  
glBegin(GL_POINTS);  
glVertex3f(1,1,0);  
glEnd();  
 

如果在上面程序段中最后一個(gè)glGetFloatv(GL_MODELVIEW_MATRIX, m)處設(shè)定斷點(diǎn)的話，就可以看到圖7所顯示的數(shù)據(jù)。

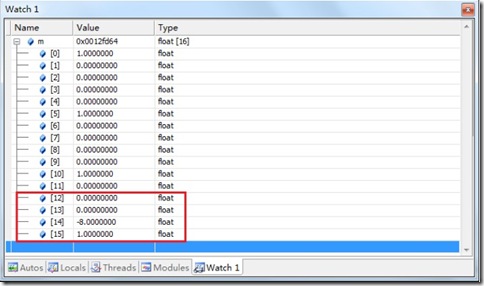圖7 ModelView變換矩陣數(shù)據(jù)

到這里，整個(gè)ModelView變換就完成了。通過ModelView變換后得到是相機(jī)坐標(biāo)系內(nèi)的坐標(biāo)。在這個(gè)坐標(biāo)系內(nèi)典型的計(jì)算就是法線了。現(xiàn)在再來看看后面一個(gè)階段。

1.2投影變換

先還是復(fù)習(xí)一下OpenGL的渲染管線。圖1中可以看到，在投影變換(Projection Transformation)中也分為兩個(gè)部分，第一個(gè)部分是將上個(gè)階段得到的坐標(biāo)轉(zhuǎn)換為平面坐標(biāo)，第二個(gè)部分是將轉(zhuǎn)換后的平面坐標(biāo)在進(jìn)行歸一化并進(jìn)行剪裁。一般地，將三維坐標(biāo)轉(zhuǎn)換為平面坐標(biāo)有兩種投影方式：正交投影(Orthogonal Projection)和透視投影(Perspective Projection)。

1.2.1 正交投影

正交投影很簡單，如圖8，對于三維空間中的坐標(biāo)點(diǎn)和一個(gè)二維平面，要在對應(yīng)的平面上投影，只需將非該平面上的點(diǎn)的坐標(biāo)分量改為該平面上的坐標(biāo)值，其余坐標(biāo)不變。

圖8 正交投影

比如將點(diǎn)(1,1,5)正交投影到z=0的平面上，那么投影后的坐標(biāo)為(1,1,0)。在openGL中，設(shè)置正交投影可以使用函數(shù):

[cpp] view plaincopy
glOrtho (GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble zNear, GLdouble zFar)  
 

該函數(shù)可以設(shè)置正交投影的投影空間，在該空間以外的坐標(biāo)點(diǎn)就不會被投影到投影平面上。函數(shù)中的六個(gè)參數(shù)分是投影空間六個(gè)平面，如圖9:

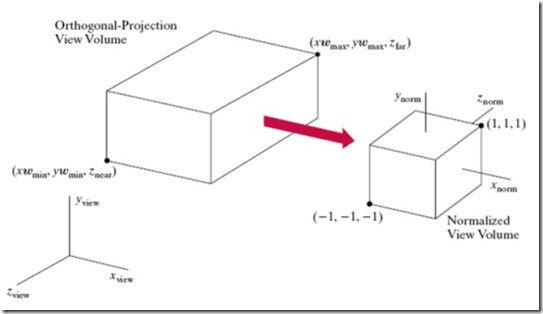
圖9 OpenGL正交投影空間和投影變換

在圖9中，大的投影空間是根據(jù)這六個(gè)參數(shù)設(shè)置的投影空間，OpenGL會自動將該空間歸一化，也就是將該空間或立方體轉(zhuǎn)化為變長為1的正六面體投影 空間，并且該證六面體的中心在相機(jī)坐標(biāo)系的原點(diǎn)。一旦設(shè)置使用glortho函數(shù)設(shè)置投影空間，OpenGL會生成投影矩陣。這個(gè)矩陣的作用就是將坐標(biāo)進(jìn) 行正交投影并且將投影后的坐標(biāo)正規(guī)化(轉(zhuǎn)換到-1到1之間)。要注意的是，生成該矩陣的時(shí)候，OpenGL會把右手坐標(biāo)系轉(zhuǎn)換為左手坐標(biāo)系。原因很簡單， 右手坐標(biāo)系的Z軸向平面外的，這樣不符合我們的習(xí)慣。該矩陣的矩陣推導(dǎo)這里就不詳細(xì)說明了，不了解的同學(xué)可以參考游戲數(shù)學(xué)方面資料，這里只給出正交投影矩 陣。

這個(gè)矩陣看來很復(fù)雜，其實(shí)計(jì)算很簡單。舉個(gè)例子，現(xiàn)在設(shè)置了這樣的正交投影空間glOrtho(-10,10,-10,10,-10,10)，這是個(gè)正六面體空間，變長為10。把這些參數(shù)帶入上面的矩陣可以得到

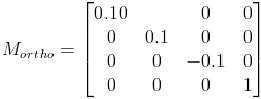現(xiàn)在還是在OpenGL程序中來檢查一下。在OpenGL程序中添加下面代碼段:

[cpp] view plaincopy
//投影設(shè)置  
glMatrixMode(GL_PROJECTION);  
glLoadIdentity();  
glOrtho(-10,10,-10,10,-10,10);  
glMatrixMode(GL_MODELVIEW);  
glGetFloatv(GL_PROJECTION_MATRIX,m)  
 

在glGetFloatv(GL_PROJECTION_MATRIX,m)處設(shè)定斷點(diǎn)就可以看到圖10中所顯示的信息。

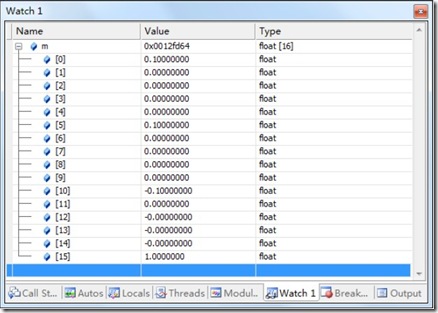圖10 正交變換矩陣數(shù)據(jù)

1.2.2透視投影

透視投影和正交投影最大的區(qū)別就是透視投影具有遠(yuǎn)近感。

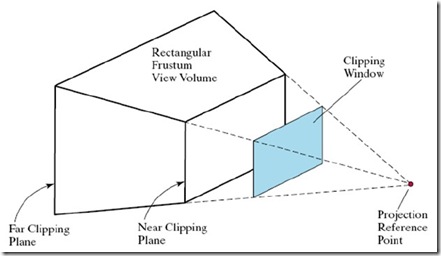
圖11 透視投影

透視投影采用了圖11中的模型，這樣的模型就是保證遠(yuǎn)的物體看起來小，近的物體看起來大。 在OpenGL中設(shè)置透視投影可以使用函數(shù):

[cpp] view plaincopy
void APIENTRY gluPerspective (GLdouble fovy, GLdouble aspect, GLdouble zNear, GLdouble zFar);  
 

該函數(shù)也會根據(jù)給定的參數(shù)生成一個(gè)投影空間。如圖11中，該投影空間是一個(gè)截頭體。同樣地，OpenGL會自動生成透視投影矩陣，該矩陣也會讓3D坐標(biāo)投影在投影平面上，并且將投影后的坐標(biāo)也進(jìn)行正規(guī)化。下面也直接給出OpenGL中使用的透視投影矩陣。

下面在OpenGL中添加下面代碼段:

[cpp] view plaincopy
//投影設(shè)置  
glMatrixMode(GL_PROJECTION);  
glLoadIdentity();  
gluPerspective(45, 1.0, 1.0, 100);  
glMatrixMode(GL_MODELVIEW);  
glGetFloatv(GL_PROJECTION_MATRIX,m)  
 

設(shè)置斷點(diǎn)后，我們可以看到圖12中顯示的數(shù)據(jù)。

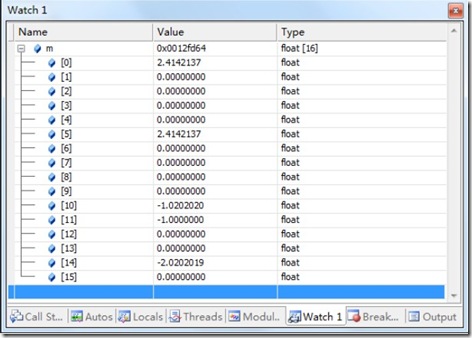圖12 透視變換矩陣數(shù)據(jù)

到此為止，整個(gè)投影變換就完成了。透過投影變換后得到的是正規(guī)化的投影平面坐標(biāo)。這為下一個(gè)階段的視口變換(View port Transformation)做好了準(zhǔn)備。

1.3視口變換

現(xiàn)在到了最后一個(gè)階段了。這個(gè)階段叫做視口變換，它把上個(gè)階段得到的正規(guī)化的投影坐標(biāo)轉(zhuǎn)化為windows 窗口坐標(biāo)。視口變換會將投影平面上的畫面映射到窗口上。在OpenGL中可以使用函數(shù)

[cpp] view plaincopy
GLAPI void GLAPIENTRY glViewport (GLint x, GLint y, GLsizei width, GLsizei height);  
 

來進(jìn)行對窗口的映射，如圖13。

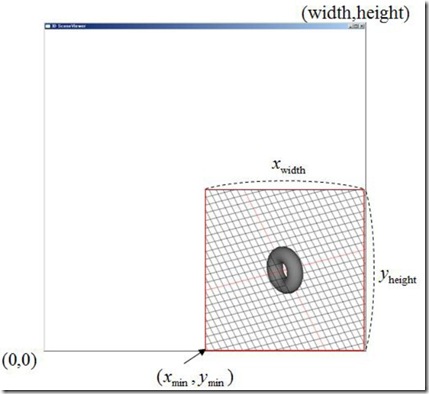
圖13 視口變換glViewport(width/2, 0, width/2, height/2)

舉個(gè)例子說明，比如上個(gè)階段中得到了一個(gè)頂點(diǎn)的坐標(biāo)為(0,0,0.5,1)，根據(jù)這個(gè)坐標(biāo)，該頂點(diǎn)位于投影平面的正中間。如果將該點(diǎn)映射到大小為 50*50的窗口上時(shí)，那么它應(yīng)該位于屏幕的中間，坐標(biāo)為(25,25, 0.5,1)。當(dāng)然這里深度值0.5是不會改變的。有的同學(xué)肯定有疑問了，既然投影到了窗口上，那么還要深度值0.5干什么？這里要注意的是，雖然在窗口 上顯示時(shí)只需要x，y坐標(biāo)就夠了，但是要在2D窗口上顯示3D圖形時(shí)深度值是不可少的。這里的深度值不是用于顯示，而是用于在光柵化的時(shí)候進(jìn)行深度測試。

OpenGL也會根據(jù)glViewport函數(shù)提供的參數(shù)值生成一個(gè)視口變換矩陣

該矩陣把上個(gè)階段得到的正規(guī)化坐標(biāo)映射到窗口上，并且將正規(guī)化坐標(biāo)中的深度值在轉(zhuǎn)換到0到1之間。所以在深度緩沖中最大值為1，最小值為0。視口變換結(jié)束 后，OpenGL中主要的圖形管線階段就算完成了，后面就是光柵化等等操作。再來回顧一下圖1，現(xiàn)在相信大家對這個(gè)渲染管線有了一定的認(rèn)識了，也明白了每 一個(gè)階段對應(yīng)的變換矩陣以及如何進(jìn)行坐標(biāo)之間的轉(zhuǎn)換的。

2. 屏幕坐標(biāo)轉(zhuǎn)換為世界坐標(biāo)

通過前面的教程，以及現(xiàn)在大家對OpenGL整個(gè)渲染管線理解后，現(xiàn)在要將屏幕上一點(diǎn)坐標(biāo)轉(zhuǎn)換為世界坐標(biāo)就比較容易了。從圖形管線的開始到結(jié)束，一 個(gè)模型坐標(biāo)系中的坐標(biāo)被轉(zhuǎn)化為了屏幕坐標(biāo)，那么現(xiàn)在把整個(gè)過程倒過來的話，屏幕上一點(diǎn)坐標(biāo)也可以轉(zhuǎn)為為世界坐標(biāo)。只要在對應(yīng)的階段求得對應(yīng)變換矩陣的逆矩 陣，就可以得到前一個(gè)階段的坐標(biāo)。這整個(gè)過程可以用圖14表示。

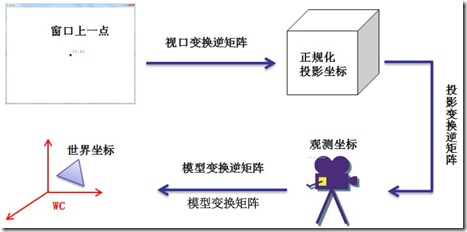圖14屏幕坐標(biāo)轉(zhuǎn)換為世界坐標(biāo)

圖中顯示的過程完全就是OpenGL渲染管線的逆過程，通過這個(gè)過程，屏幕上的點(diǎn)就可以轉(zhuǎn)化為世界坐標(biāo)系中的點(diǎn)了。可能又有的同學(xué)要問，當(dāng)鼠標(biāo)點(diǎn)擊屏幕上一點(diǎn)的時(shí)候并沒有深度信息，轉(zhuǎn)換的時(shí)候要怎么辦呢？這個(gè)時(shí)候可以使用OpenGL函數(shù)

[cpp] view plaincopy
void glReadPixels (GLint x, GLint y, GLsizei width, GLsizei height, GLenum format, GLenum type, GLvoid *pixels);  
 

該函數(shù)能夠獲得屏幕上一點(diǎn)對應(yīng)像素的深度信息。有了這個(gè)深度信息，就可以利用上面過程把屏幕上一點(diǎn)轉(zhuǎn)換為世界坐標(biāo)了。在OpenGL中，上面的過程其實(shí)已經(jīng)有現(xiàn)成的函數(shù)可以使用，那就是

[cpp] view plaincopy
int APIENTRY gluUnProject (  
    GLdouble  winx, GLdouble  winy,  
    GLdouble  winz,  
    const GLdouble modelMatrix[16],  
    const GLdouble projMatrix[16],  
    const GLint    viewport[4],  
    GLdouble  *objx,  GLdouble  *objy,  
    GLdouble       *objz);  
 

該函數(shù)直接將屏幕上一點(diǎn)轉(zhuǎn)換對應(yīng)的世界坐標(biāo)，該函數(shù)的內(nèi)部實(shí)現(xiàn)其實(shí)還是上面的那么逆過程。下面給出利用該函數(shù)獲取世界坐標(biāo)的代碼段。

[cpp] view plaincopy
GVector screen2world(int x, int y)  
{  
       GLint viewport[4];  
       GLdouble modelview[16];  
       GLdouble projection[16];  
       GLfloat winX, winY, winZ;  
       GLdouble posX, posY, posZ;  
       glGetDoublev(GL_MODELVIEW_MATRIX, modelview);  
       glGetDoublev(GL_PROJECTION_MATRIX, projection);  
       glGetIntegerv(GL_VIEWPORT, viewport);  
       winX = (float)x;  
       winY = (float)viewport[3] - (float)y;  
       glReadPixels(x, int(winY), 1, 1, GL_DEPTH_COMPONENT, GL_FLOAT, &winZ);  
       gluUnProject(winX, winY, winZ, modelview, projection, viewport, &posX, &posY, &posZ);  
       GVector v(4, posX, posY, posZ, 1.0);  
       return v;  
}  
 

代碼中函數(shù)返回類型GVector是用戶定義的向量類，返回的是齊次坐標(biāo)。