投影矩陣的實(shí)現(xiàn)以及如何從投影矩陣中獲取各視裁體平面(教程):
flipcode@msn.com
一．投影的實(shí)現(xiàn)：
以D3D為例，先看一下D3D有前設(shè)置投影矩陣參數(shù)的函數(shù)：
D3DXMATRIX *WINAPI D3DXMatrixPerspectiveFovLH(
D3DXMATRIX *pOut,
FLOAT fovy,
FLOAT Aspect,
FLOAT zn,
FLOAT zf
);
第一個(gè)是輸出的結(jié)果，第二個(gè)是視角，第三個(gè)是屏幕寬高比，第四個(gè)是近平面，第五個(gè)是遠(yuǎn)平面．
其實(shí)如果不用作視裁剪，只作屏幕投影的話只需用到fovy和aspect，下面我們先求ys的投影，而求出
ys后x的投影xs我們只需根據(jù)屏幕寬高比aspect來作一下調(diào)整就可以了．
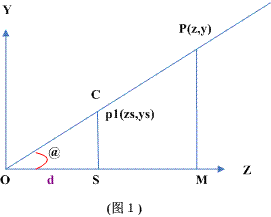
(圖１)
o = camera's postion
SC = screen's upper half hight (i.e. screen height/2)
p = a point will project to our screen
d = OS (the distance from O to S)
下面來求ys:
由于OSP1與OMP相似，故
d/z = ys/y
轉(zhuǎn)換一下,得：
ys = d*y/z
現(xiàn)在只差一個(gè)未知的d了,
那么d怎么求呢？下面來看一個(gè)圖：
o = camera's postion
SC = screen's upper half hight (i.e. screen height/2)
d = OA (the distance from O to A)
@ = fov/2
從上圖可知tag(@)=SC/d即tag(fov/2)=SC/d，其中fov是已知的（由參數(shù)傳進(jìn)），
那么SC呢？查看D3D的文檔知道D3D的project空間的
可視范圍定義為x∈[-1,1], y∈[-1,1], z∈[0,1]的一個(gè)長方體(下面圖２和圖３)。
(注:ogl的是z∈[[1,1])
從project空間的z負(fù)半軸看看我們的變換目標(biāo)
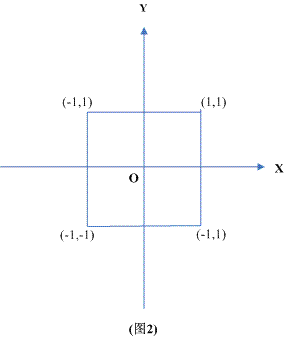
從project空間的x正半軸看看我們的變換目標(biāo)
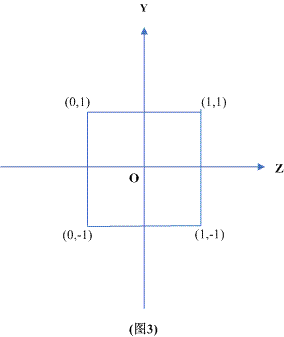
這可看作中間坐標(biāo)系，從這個(gè)坐標(biāo)系到屏幕坐標(biāo)只需作放縮和平移操作即可
這樣定義的好處是避免一些設(shè)備相關(guān)性的東西來分散我們的注意力，集中把算法
弄好后而在最后再作調(diào)整就可以了．
從上圖看出SC=1,故d=1/tag(fov/2)=cot(fov/2);
好，經(jīng)過這么一番折騰我們最終得到了ys= y*d/z=y*cot(fov/2)/z;
而xs計(jì)算同理，但是由于屏幕寬高實(shí)際上是不等的，所以可通過參數(shù)aspect縱橫比
進(jìn)行調(diào)整，xs=x*cot(fov/2)/z/aspect;，另外為了得以使用矩陣乘法，
我們可以利用w分量來保存z(因?yàn)閣分量在投影矩陣之前都沒用到過),
最后才讓x/w,y/w來得到正確的投影值，
從而可以得到矩陣如下：
d/aspect 0 0 0
0 d 0 0
0 0 1 1
0 0 0 0
(其中d=cot(fov/2))
二．裁剪:
由上面矩陣我們就可以將一個(gè)三維的物體坐標(biāo)轉(zhuǎn)投影轉(zhuǎn)換到二維的屏幕空間了，但是為了
去掉那些離攝象相很近或是在攝象機(jī)后面（投影會(huì)變反）或是離攝像很遠(yuǎn)的物體從而減輕
渲染的負(fù)擔(dān)（以及修正反向投影），我們還要處理一個(gè)要投影到(0-1)的z分量.
而這個(gè)時(shí)候就要用到D3DXMatrixPerspectiveFovLH的最后兩個(gè)參數(shù)了（i.e.近平面及遠(yuǎn)平面）
下面來討論它:
如圖：
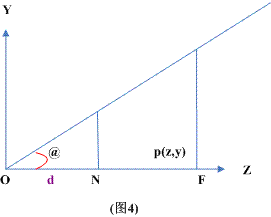
o = camera's postion
@ = fov/2
N = near plane
F = far plane
p = a point will project to our screen
從上圖可以看到N就是我們要作裁剪用的近平面，而F就是我們要作裁剪用遠(yuǎn)平面，
近平面和遠(yuǎn)平面可從參數(shù)得來，這時(shí)我們想作的是讓落在N和F上的點(diǎn)映射到０到１的
線性坐標(biāo)上，也就是說當(dāng)p的z=N時(shí)投影后的zs=0,而當(dāng)z=F時(shí)投影后的zs=1;
這個(gè)很好辦：zs=(z-N)/(F-N)即可.
好了，這一步也輕松辦到了，但是我們前面為了實(shí)際用矩陣變換來作投影而讓其在
投影后再/w（w保存z值）才是最后的結(jié)果. 既然這樣那么我們所求的就是還未除過w的
投影值為zw. 想一下，當(dāng)z=F時(shí)我們投影后的zs=zw/z=1，也就是zs=zw/F=1;所以zw=zs*F,
因?yàn)榍懊媲蟮脄s=(z-N)/(F-N)，所以zw=F*(z-N)/(F-N);（簡(jiǎn)單驗(yàn)證一下：當(dāng)z=N時(shí)，zw=0,這時(shí)
zs=0/w還是０，而當(dāng)z增大時(shí)0<zw<=F,也就是0<zs<=1,而直到z=F時(shí)，zw=F,這時(shí)zs=F/w=F/F=1），
為了方便將其分解成:zw=(z*F-N*F)/(F-N)=z*F/(F-N)-N*F/(F-N)
這樣就可以把它應(yīng)用到矩陣中，如下：
d/aspect 0 0 0
0 d 0 0
0 0 F/(F-N) 1
0 0 -N*F/(F-N) 0
以上公式可以代替D3DXMatrixPerspectiveFovLH來作測(cè)試：
void myMatrixPerspectiveFovLH(mat4 *out, float fov, float aspect, float n, float f)
{
float h = tanf(0.5*fov);
float w = h * aspect;
out = mat4( 1.0f/w, 0, 0, 0
0 1.0f/h 0 0
0 0 f/(f-n) 1
0 0 -n*f/(f-n) 0);
}
其中1.0f/h 就是cot(fov/2), aspect=width/height
三．從投影矩陣獲取視裁體:
上面已說過對(duì)一點(diǎn)投影后的各分量值所在范圍為:
-1<xs<1;
-1<ys<1;
0<zs<1;
其中xs/ys/zs是除過w后的值，而未除過w的值所在范圍是：
-w<xw<w; -w<yw<w;
0<zw<w;
對(duì)各不等式進(jìn)分解后得:
xw+w>0;且xw-w<0;
yw+w>0;且yw-w<0;
zw>0;且xw-w<0;
我們知道xw/yw/zw是一個(gè)在view space中的點(diǎn)v(xv,yv,zv,wv)(其中wv=1)乘上投影矩陣后的各分量值（當(dāng)然還未除以w）,那么
點(diǎn)v(xv,yv,zv,wv)是如何乘上投影矩陣的呢？是這樣的：
xw = xv*prj_11+yv*prj_21*prj_31+wv*prj_41;
zw = xv*prj_12+yv*prj_22*prj_32+wv*prj_42;
zw = xv*prj_13+yv*prj_23*prj_33+wv*prj_43;
w = xv*prj_14+yv*prj_24*prj_34+wv*prj_44;
即:
xw = v dop col1;
yw = v dop col2;
zw = v dop col3;
w = v dop col4;
(說明：上述col1和col2及col3其實(shí)表達(dá)了一個(gè)投影坐標(biāo)系，其中col1表示x軸，col2表示y軸,col3表示z軸,
而點(diǎn)v乘上這個(gè)坐標(biāo)系就相當(dāng)于求出點(diǎn)v在此新坐標(biāo)系中各分量上的投影值，此外col4只是簡(jiǎn)單的為了讓點(diǎn)v點(diǎn)乘它時(shí)求得w=原點(diǎn)v的w分量值)
故：
xw+w>0;
即：
v dop col1 + v dop col4 > 0;
即：
v dop ( col1 + col4 ) > 0;
也就是：
xv*(prj_11+prj_14) + yv*(prj_21+prj_24) + zv*(prj_31+prj_34) + wv*(prj_41+prj_44) > 0;
我們知道平面公式是： ax+by+cz+d=0，故上面其實(shí)表示的就是視裁體的左平面向內(nèi)，其中它的法線是：
(prj_11+prj_14), (prj_21+prj_24), (prj_31+prj_34).
而由于wv=1,
故它的距離是(prj_41+prj_44)．
同理我們可以求出視裁體的其它平面．
四．Frustum Culling
我們知道，視裁體的六個(gè)面是朝向內(nèi)的，由上面已經(jīng)得到了各平面等式，只要用P DOP N + D看是否大于０就可以知道點(diǎn)Ｐ是否在一個(gè)平面
內(nèi)，最后點(diǎn)Ｐ如果在所有平面內(nèi)的才是在視裁體內(nèi)．
而當(dāng)判斷一個(gè)物體是否在視裁體內(nèi)時(shí)，我們只需對(duì)物體的包圍盒進(jìn)行測(cè)試，例如，測(cè)試一個(gè)包圍球是否在視裁體內(nèi)，只要判斷所有P DOP N + D
＞2的1/2次方*R不等式成立即可．
參考文檔:
fast extraction of viewing frustum planes from the world-view-projection matrix