一步一步寫(xiě)平衡二叉樹(shù)（AVL樹(shù)）
作者：C小加 更新時(shí)間：2012-8-20
平衡二叉樹(shù)（Balanced Binary Tree）是二叉查找樹(shù)的一個(gè)進(jìn)化體，也是第一個(gè)引入平衡概念的二叉樹(shù)。1962年，G.M. Adelson-Velsky 和 E.M. Landis發(fā)明了這棵樹(shù)，所以它又叫AVL樹(shù)。平衡二叉樹(shù)要求對(duì)于每一個(gè)節(jié)點(diǎn)來(lái)說(shuō)，它的左右子樹(shù)的高度之差不能超過(guò)1，如果插入或者刪除一個(gè)節(jié)點(diǎn)使得高度之差大于1，就要進(jìn)行節(jié)點(diǎn)之間的旋轉(zhuǎn)，將二叉樹(shù)重新維持在一個(gè)平衡狀態(tài)。這個(gè)方案很好的解決了二叉查找樹(shù)退化成鏈表的問(wèn)題，把插入，查找，刪除的時(shí)間復(fù)雜度最好情況和最壞情況都維持在O(logN)。但是頻繁旋轉(zhuǎn)會(huì)使插入和刪除犧牲掉O(logN)左右的時(shí)間，不過(guò)相對(duì)二叉查找樹(shù)來(lái)說(shuō)，時(shí)間上穩(wěn)定了很多。
平衡二叉樹(shù)實(shí)現(xiàn)的大部分過(guò)程和二叉查找樹(shù)是一樣的（學(xué)平衡二叉樹(shù)之前一定要會(huì)二叉查找樹(shù)），區(qū)別就在于插入和刪除之后要寫(xiě)一個(gè)旋轉(zhuǎn)算法去維持平衡，維持平衡需要借助一個(gè)節(jié)點(diǎn)高度的屬性。我參考了機(jī)械工業(yè)出版社的《數(shù)據(jù)結(jié)構(gòu)與算法分析-C語(yǔ)言描述》寫(xiě)了一個(gè)C++版的代碼。這本書(shū)的AVLTree講的很好，不過(guò)沒(méi)有很完整的去描述。我會(huì)一步一步的講解如何寫(xiě)平衡二叉樹(shù)，重點(diǎn)是平衡二叉樹(shù)的核心部分，也就是旋轉(zhuǎn)算法。
第一步：節(jié)點(diǎn)信息
相對(duì)于二叉查找樹(shù)的節(jié)點(diǎn)來(lái)說(shuō)，我們需要用一個(gè)屬性二叉樹(shù)的高度，目的是維護(hù)插入和刪除過(guò)程中的旋轉(zhuǎn)算法。
代碼如下：
//AVL樹(shù)節(jié)點(diǎn)信息
template<class T>
class TreeNode
{
public:
TreeNode():lson(NULL),rson(NULL),freq(1),hgt(0){}
T data;//值
int hgt;//以此節(jié)點(diǎn)為根的樹(shù)的高度
unsigned int freq;//頻率
TreeNode* lson;//指向左兒子的地址
TreeNode* rson;//指向右兒子的地址
};
第二步：平衡二叉樹(shù)類的聲明
聲明中的旋轉(zhuǎn)函數(shù)將在后邊的步驟中詳解。
代碼如下：
//AVL樹(shù)類的屬性和方法聲明
template<class T>
class AVLTree
{
private:
TreeNode<T>* root;//根節(jié)點(diǎn)
void insertpri(TreeNode<T>* &node,T x);//插入
TreeNode<T>* findpri(TreeNode<T>* node,T x);//查找
void insubtree(TreeNode<T>* node);//中序遍歷
void Deletepri(TreeNode<T>* &node,T x);//刪除
int height(TreeNode<T>* node);//求樹(shù)的高度
void SingRotateLeft(TreeNode<T>* &k2);//左左情況下的旋轉(zhuǎn)
void SingRotateRight(TreeNode<T>* &k2);//右右情況下的旋轉(zhuǎn)
void DoubleRotateLR(TreeNode<T>* &k3);//左右情況下的旋轉(zhuǎn)
void DoubleRotateRL(TreeNode<T>* &k3);//右左情況下的旋轉(zhuǎn)
int Max(int cmpa,int cmpb);//求最大值
public:
AVLTree():root(NULL){}
void insert(T x);//插入接口
TreeNode<T>* find(T x);//查找接口
void Delete(T x);//刪除接口
void traversal();//遍歷接口
};
第三步：兩個(gè)輔助方法
旋轉(zhuǎn)算法需要借助于兩個(gè)功能的輔助，一個(gè)是求樹(shù)的高度，一個(gè)是求兩個(gè)高度的最大值。這里規(guī)定，一棵空樹(shù)的高度為-1，只有一個(gè)根節(jié)點(diǎn)的樹(shù)的高度為0，以后每多一層高度加1。為了解決指針NULL這種情況，寫(xiě)了一個(gè)求高度的函數(shù)，這個(gè)函數(shù)還是很有必要的。
代碼如下：
//計(jì)算以節(jié)點(diǎn)為根的樹(shù)的高度
template<class T>
int AVLTree<T>::height(TreeNode<T>* node)
{
if(node!=NULL)
return node->hgt;
return -1;
}
//求最大值
template<class T>
int AVLTree<T>::Max(int cmpa,int cmpb)
{
return cmpa>cmpb?cmpa:cmpb;
}
第四步：旋轉(zhuǎn)
對(duì)于一個(gè)平衡的節(jié)點(diǎn)，由于任意節(jié)點(diǎn)最多有兩個(gè)兒子，因此高度不平衡時(shí)，此節(jié)點(diǎn)的兩顆子樹(shù)的高度差2.容易看出，這種不平衡出現(xiàn)在下面四種情況：
1、6節(jié)點(diǎn)的左子樹(shù)3節(jié)點(diǎn)高度比右子樹(shù)7節(jié)點(diǎn)大2，左子樹(shù)3節(jié)點(diǎn)的左子樹(shù)1節(jié)點(diǎn)高度大于右子樹(shù)4節(jié)點(diǎn)，這種情況成為左左。
2、6節(jié)點(diǎn)的左子樹(shù)2節(jié)點(diǎn)高度比右子樹(shù)7節(jié)點(diǎn)大2，左子樹(shù)2節(jié)點(diǎn)的左子樹(shù)1節(jié)點(diǎn)高度小于右子樹(shù)4節(jié)點(diǎn)，這種情況成為左右。
3、2節(jié)點(diǎn)的左子樹(shù)1節(jié)點(diǎn)高度比右子樹(shù)5節(jié)點(diǎn)小2，右子樹(shù)5節(jié)點(diǎn)的左子樹(shù)3節(jié)點(diǎn)高度大于右子樹(shù)6節(jié)點(diǎn)，這種情況成為右左。
4、2節(jié)點(diǎn)的左子樹(shù)1節(jié)點(diǎn)高度比右子樹(shù)4節(jié)點(diǎn)小2，右子樹(shù)4節(jié)點(diǎn)的左子樹(shù)3節(jié)點(diǎn)高度小于右子樹(shù)6節(jié)點(diǎn)，這種情況成為右右。
從圖2中可以可以看出，1和4兩種情況是對(duì)稱的，這兩種情況的旋轉(zhuǎn)算法是一致的，只需要經(jīng)過(guò)一次旋轉(zhuǎn)就可以達(dá)到目標(biāo)，我們稱之為單旋轉(zhuǎn)。2和3兩種情況也是對(duì)稱的，這兩種情況的旋轉(zhuǎn)算法也是一致的，需要進(jìn)行兩次旋轉(zhuǎn)，我們稱之為雙旋轉(zhuǎn)。
第五步：?jiǎn)涡D(zhuǎn)
單旋轉(zhuǎn)是針對(duì)于左左和右右這兩種情況的解決方案，這兩種情況是對(duì)稱的，只要解決了左左這種情況，右右就很好辦了。圖3是左左情況的解決方案，節(jié)點(diǎn)k2不滿足平衡特性，因?yàn)樗淖笞訕?shù)k1比右子樹(shù)Z深2層，而且k1子樹(shù)中，更深的一層的是k1的左子樹(shù)X子樹(shù)，所以屬于左左情況。
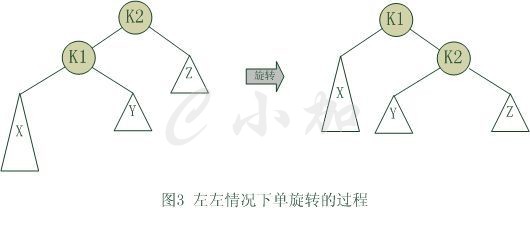
為使樹(shù)恢復(fù)平衡，我們把k2變成這棵樹(shù)的根節(jié)點(diǎn)，因?yàn)閗2大于k1，把k2置于k1的右子樹(shù)上，而原本在k1右子樹(shù)的Y大于k1，小于k2，就把Y置于k2的左子樹(shù)上，這樣既滿足了二叉查找樹(shù)的性質(zhì)，又滿足了平衡二叉樹(shù)的性質(zhì)。
這樣的操作只需要一部分指針改變，結(jié)果我們得到另外一顆二叉查找樹(shù)，它是一棵AVL樹(shù)，因?yàn)閄向上一移動(dòng)了一層，Y還停留在原來(lái)的層面上，Z向下移動(dòng)了一層。整棵樹(shù)的新高度和之前沒(méi)有在左子樹(shù)上插入的高度相同，插入操作使得X高度長(zhǎng)高了。因此，由于這顆子樹(shù)高度沒(méi)有變化，所以通往根節(jié)點(diǎn)的路徑就不需要繼續(xù)旋轉(zhuǎn)了。
代碼如下：
//左左情況下的旋轉(zhuǎn)
template<class T>
void AVLTree<T>::SingRotateLeft(TreeNode<T>* &k2)
{
TreeNode<T>* k1;
k1=k2->lson;
k2->lson=k1->rson;
k1->rson=k2;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->lson),k2->hgt)+1;
}
//右右情況下的旋轉(zhuǎn)
template<class T>
void AVLTree<T>::SingRotateRight(TreeNode<T>* &k2)
{
TreeNode<T>* k1;
k1=k2->rson;
k2->rson=k1->lson;
k1->lson=k2;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->rson),k2->hgt)+1;
}
第六步：雙旋轉(zhuǎn)
對(duì)于左右和右左這兩種情況，單旋轉(zhuǎn)不能使它達(dá)到一個(gè)平衡狀態(tài)，要經(jīng)過(guò)兩次旋轉(zhuǎn)。雙旋轉(zhuǎn)是針對(duì)于這兩種情況的解決方案，同樣的，這樣兩種情況也是對(duì)稱的，只要解決了左右這種情況，右左就很好辦了。圖4是左右情況的解決方案，節(jié)點(diǎn)k3不滿足平衡特性，因?yàn)樗淖笞訕?shù)k1比右子樹(shù)Z深2層，而且k1子樹(shù)中，更深的一層的是k1的右子樹(shù)k2子樹(shù)，所以屬于左右情況。
為使樹(shù)恢復(fù)平衡，我們需要進(jìn)行兩步，第一步，把k1作為根，進(jìn)行一次右右旋轉(zhuǎn)，旋轉(zhuǎn)之后就變成了左左情況，所以第二步再進(jìn)行一次左左旋轉(zhuǎn)，最后得到了一棵以k2為根的平衡二叉樹(shù)樹(shù)。
代碼如下：
//左右情況的旋轉(zhuǎn)
template<class T>
void AVLTree<T>::DoubleRotateLR(TreeNode<T>* &k3)
{
SingRotateRight(k3->lson);
SingRotateLeft(k3);
}
//右左情況的旋轉(zhuǎn)
template<class T>
void AVLTree<T>::DoubleRotateRL(TreeNode<T>* &k3)
{
SingRotateLeft(k3->rson);
SingRotateRight(k3);
}
第七步：插入
插入的方法和二叉查找樹(shù)基本一樣，區(qū)別是，插入完成后需要從插入的節(jié)點(diǎn)開(kāi)始維護(hù)一個(gè)到根節(jié)點(diǎn)的路徑，每經(jīng)過(guò)一個(gè)節(jié)點(diǎn)都要維持樹(shù)的平衡。維持樹(shù)的平衡要根據(jù)高度差的特點(diǎn)選擇不同的旋轉(zhuǎn)算法。
代碼如下：
//插入
template<class T>
void AVLTree<T>::insertpri(TreeNode<T>* &node,T x)
{
if(node==NULL)//如果節(jié)點(diǎn)為空,就在此節(jié)點(diǎn)處加入x信息
{
node=new TreeNode<T>();
node->data=x;
return;
}
if(node->data>x)//如果x小于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的左子樹(shù)中插入x
{
insertpri(node->lson,x);
if(2==height(node->lson)-height(node->rson))
if(x<node->lson->data)
SingRotateLeft(node);
else
DoubleRotateLR(node);
}
else if(node->data<x)//如果x大于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的右子樹(shù)中插入x
{
insertpri(node->rson,x);
if(2==height(node->rson)-height(node->lson))//如果高度之差為2的話就失去了平衡,需要旋轉(zhuǎn)
if(x>node->rson->data)
SingRotateRight(node);
else
DoubleRotateRL(node);
}
else ++(node->freq);//如果相等,就把頻率加1
node->hgt=Max(height(node->lson),height(node->rson));
}
//插入接口
template<class T>
void AVLTree<T>::insert(T x)
{
insertpri(root,x);
}
第八步：查找
和二叉查找樹(shù)相比，查找方法沒(méi)有變法，不過(guò)根據(jù)存儲(chǔ)的特性，AVL樹(shù)能維持在一個(gè)O(logN)的穩(wěn)定的時(shí)間，而二叉查找樹(shù)則相當(dāng)不穩(wěn)定。
代碼如下：
//查找
template<class T>
TreeNode<T>* AVLTree<T>::findpri(TreeNode<T>* node,T x)
{
if(node==NULL)//如果節(jié)點(diǎn)為空說(shuō)明沒(méi)找到,返回NULL
{
return NULL;
}
if(node->data>x)//如果x小于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的左子樹(shù)中查找x
{
return findpri(node->lson,x);
}
else if(node->data<x)//如果x大于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的左子樹(shù)中查找x
{
return findpri(node->rson,x);
}
else return node;//如果相等,就找到了此節(jié)點(diǎn)
}
//查找接口
template<class T>
TreeNode<T>* AVLTree<T>::find(T x)
{
return findpri(root,x);
}
第九步：刪除
刪除的方法也和二叉查找樹(shù)的一致，區(qū)別是，刪除完成后，需要從刪除節(jié)點(diǎn)的父親開(kāi)始向上維護(hù)樹(shù)的平衡一直到根節(jié)點(diǎn)。
代碼如下：
//刪除
template<class T>
void AVLTree<T>::Deletepri(TreeNode<T>* &node,T x)
{
if(node==NULL) return ;//沒(méi)有找到值是x的節(jié)點(diǎn)
if(x < node->data)
{
Deletepri(node->lson,x);//如果x小于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的左子樹(shù)中刪除x
if(2==height(node->rson)-height(node->lson))
if(node->rson->lson!=NULL&&(height(node->rson->lson)>height(node->rson->rson)) )
DoubleRotateRL(node);
else
SingRotateRight(node);
}
else if(x > node->data)
{
Deletepri(node->rson,x);//如果x大于節(jié)點(diǎn)的值,就繼續(xù)在節(jié)點(diǎn)的右子樹(shù)中刪除x
if(2==height(node->lson)-height(node->rson))
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
DoubleRotateLR(node);
else
SingRotateLeft(node);
}
else//如果相等,此節(jié)點(diǎn)就是要?jiǎng)h除的節(jié)點(diǎn)
{
if(node->lson&&node->rson)//此節(jié)點(diǎn)有兩個(gè)兒子
{
TreeNode<T>* temp=node->rson;//temp指向節(jié)點(diǎn)的右兒子
while(temp->lson!=NULL) temp=temp->lson;//找到右子樹(shù)中值最小的節(jié)點(diǎn)
//把右子樹(shù)中最小節(jié)點(diǎn)的值賦值給本節(jié)點(diǎn)
node->data=temp->data;
node->freq=temp->freq;
Deletepri(node->rson,temp->data);//刪除右子樹(shù)中最小值的節(jié)點(diǎn)
if(2==height(node->lson)-height(node->rson))
{
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
DoubleRotateLR(node);
else
SingRotateLeft(node);
}
}
else//此節(jié)點(diǎn)有1個(gè)或0個(gè)兒子
{
TreeNode<T>* temp=node;
if(node->lson==NULL)//有右兒子或者沒(méi)有兒子
node=node->rson;
else if(node->rson==NULL)//有左兒子
node=node->lson;
delete(temp);
temp=NULL;
}
}
if(node==NULL) return;
node->hgt=Max(height(node->lson),height(node->rson))+1;
return;
}
//刪除接口
template<class T>
void AVLTree<T>::Delete(T x)
{
Deletepri(root,x);
}
第十步：中序遍歷
代碼如下：
//中序遍歷函數(shù)
template<class T>
void AVLTree<T>::insubtree(TreeNode<T>* node)
{
if(node==NULL) return;
insubtree(node->lson);//先遍歷左子樹(shù)
cout<<node->data<<" ";//輸出根節(jié)點(diǎn)
insubtree(node->rson);//再遍歷右子樹(shù)
}
//中序遍歷接口
template<class T>
void AVLTree<T>::traversal()
{
insubtree(root);
}
第十一步：關(guān)于效率
此數(shù)據(jù)結(jié)構(gòu)插入、查找和刪除的時(shí)間復(fù)雜度均為O(logN)，但是插入和刪除需要額外的旋轉(zhuǎn)算法需要的時(shí)間，有時(shí)旋轉(zhuǎn)過(guò)多也會(huì)影響效率。
關(guān)于遞歸和非遞歸。我用的是遞歸的方法進(jìn)行插入，查找和刪除，而非遞歸的方法一般來(lái)說(shuō)要比遞歸的方法快很多，但是我感覺(jué)非遞歸的方法寫(xiě)出來(lái)會(huì)比較困難，所以我還是選擇了遞歸的方法。
還有一種效率的問(wèn)題是關(guān)于高度信息的存儲(chǔ)，由于我們需要的僅僅是高度的差，不需要知道這棵樹(shù)的高度，所以只需要使用兩個(gè)二進(jìn)制位就可以表示這個(gè)差。這樣可以避免平衡因子的重復(fù)計(jì)算，可以稍微的加快一些速度，不過(guò)代碼也喪失了相對(duì)簡(jiǎn)明性和清晰度。如果采用遞歸寫(xiě)法的話，這種微加速就更顯得微乎其微了。
如果有哪些不對(duì)的或者不清晰的地方請(qǐng)指出，我會(huì)修改并加以完善。
附：完整代碼