一步一步寫二叉查找樹
作者:C小加 更新時間:2012-8-9
二叉查找樹(BST)是二叉樹的一個重要的應用,它在二叉樹的基礎(chǔ)上加上了這樣的一個性質(zhì):對于樹中的每一個節(jié)點來說,如果有左兒子的話,它的左兒子的值一定小于它本身的值,如果有右兒子的話,它的右兒子的值一定大于它本身的值。
二叉查找樹的操作一般有插入、刪除和查找,這幾個操作的平均時間復雜度都為O(logn),插入和查找操作很簡單,刪除操作會復雜一點,除此之外,因為二叉樹的中序遍歷是一個有序序列,我就額外加上了一個中序遍歷操作。
二叉查找樹的應用不是很多,因為它最壞的時候跟線性表差不多,大部分會應用到它的升級版,平衡二叉樹和紅黑樹,這兩棵樹都能把時間復雜度穩(wěn)定在O(logn)左右。雖然不會用到,但是二叉查找樹是一定要學好的,畢竟它是平衡二叉樹和紅黑樹的基礎(chǔ)。
接下來一步一步寫一個二叉查找樹模板。完整代碼下載
第一步:節(jié)點信息
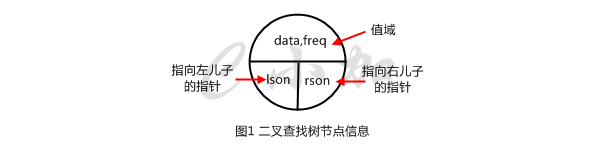
二叉查找樹的節(jié)點和二叉樹的節(jié)點大部分是一樣的,不同的是,二叉查找樹多了一個值出現(xiàn)的次數(shù)。如圖1顯示了二叉查找樹的節(jié)點信息。
代碼如下:
//二叉查找樹節(jié)點信息
template<class T>
class TreeNode
{
public:
TreeNode():lson(NULL),rson(NULL),freq(1){}//初始化
T data;//值
unsigned int freq;//頻率
TreeNode* lson;//指向左兒子的坐標
TreeNode* rson;//指向右兒子的坐標
};
第二步:二叉查找樹類的聲明
代碼如下:
//二叉查找樹類的屬性和方法聲明
template<class T>
class BST
{
private:
TreeNode<T>* root;//根節(jié)點
void insertpri(TreeNode<T>* &node,T x);//插入
TreeNode<T>* findpri(TreeNode<T>* node,T x);//查找
void insubtree(TreeNode<T>* node);//中序遍歷
void Deletepri(TreeNode<T>* &node,T x);//刪除
public:
BST():root(NULL){}
void insert(T x);//插入接口
TreeNode<T>* find(T x);//查找接口
void Delete(T x);//刪除接口
void traversal();//遍歷接口
};
第三步:插入
根據(jù)二叉查找樹的性質(zhì),插入一個節(jié)點的時候,如果根節(jié)點為空,就此節(jié)點作為根節(jié)點,如果根節(jié)點不為空,就要先和根節(jié)點比較,如果比根節(jié)點的值小,就插入到根節(jié)點的左子樹中,如果比根節(jié)點的值大就插入到根節(jié)點的右子樹中,如此遞歸下去,找到插入的位置。重復節(jié)點的插入用值域中的freq標記。如圖2是一個插入的過程。
二叉查找樹的時間復雜度要看這棵樹的形態(tài),如果比較接近一一棵完全二叉樹,那么時間復雜度在O(logn)左右,如果遇到如圖3這樣的二叉樹的話,那么時間復雜度就會恢復到線性的O(n)了。
平衡二叉樹會很好的解決如圖3這種情況。
插入函數(shù)的代碼如下:
//插入
template<class T>
void BST<T>::insertpri(TreeNode<T>* &node,T x)
{
if(node==NULL)//如果節(jié)點為空,就在此節(jié)點處加入x信息
{
node=new TreeNode<T>();
node->data=x;
return;
}
if(node->data>x)//如果x小于節(jié)點的值,就繼續(xù)在節(jié)點的左子樹中插入x
{
insertpri(node->lson,x);
}
else if(node->data<x)//如果x大于節(jié)點的值,就繼續(xù)在節(jié)點的右子樹中插入x
{
insertpri(node->rson,x);
}
else ++(node->freq);//如果相等,就把頻率加1
}
//插入接口
template<class T>
void BST<T>::insert(T x)
{
insertpri(root,x);
}
第四步:查找
查找的功能和插入差不多一樣,按照插入那樣的方式遞歸下去,如果找到了,就返回這個節(jié)點的地址,如果沒有找到,就返回NULL。
代碼如下:
//查找
template<class T>
TreeNode<T>* BST<T>::findpri(TreeNode<T>* node,T x)
{
if(node==NULL)//如果節(jié)點為空說明沒找到,返回NULL
{
return NULL;
}
if(node->data>x)//如果x小于節(jié)點的值,就繼續(xù)在節(jié)點的左子樹中查找x
{
return findpri(node->lson,x);
}
else if(node->data<x)//如果x大于節(jié)點的值,就繼續(xù)在節(jié)點的左子樹中查找x
{
return findpri(node->rson,x);
}
else return node;//如果相等,就找到了此節(jié)點
}
//查找接口
template<class T>
TreeNode<T>* BST<T>::find(T x)
{
return findpri(root,x);
}
第五步:刪除
刪除會麻煩一點,如果是葉子節(jié)點的話,直接刪除就可以了。如果只有一個孩子的話,就讓它的父親指向它的兒子,然后刪除這個節(jié)點。圖4顯示了一棵初始樹和4節(jié)點被刪除后的結(jié)果。先用一個臨時指針指向4節(jié)點,再讓4節(jié)點的地址指向它的孩子,這個時候2節(jié)點的右兒子就變成了3節(jié)點,最后刪除臨時節(jié)點指向的空間,也就是4節(jié)點。
刪除有兩個兒子的節(jié)點會比較復雜一些。一般的刪除策略是用其右子樹最小的數(shù)據(jù)代替該節(jié)點的數(shù)據(jù)并遞歸的刪除掉右子樹中最小數(shù)據(jù)的節(jié)點。因為右子樹中數(shù)據(jù)最小的節(jié)點肯定沒有左兒子,所以刪除的時候容易一些。圖5顯示了一棵初始樹和2節(jié)點被刪除后的結(jié)果。首先在2節(jié)點的右子樹中找到最小的節(jié)點3,然后把3的數(shù)據(jù)賦值給2節(jié)點,這個時候2節(jié)點的數(shù)據(jù)變?yōu)?/span>3,然后的工作就是刪除右子樹中的3節(jié)點了,采用遞歸刪除。
我們發(fā)現(xiàn)對2節(jié)點右子樹的查找進行了兩遍,第一遍找到最小節(jié)點并賦值,第二遍刪除這個最小的節(jié)點,這樣的效率并不是很高。你能不能寫出只查找一次就可以實現(xiàn)賦值和刪除兩個功能的函數(shù)呢?
如果刪除的次數(shù)不是很多的話,有一種刪除的方法會比較快一點,名字叫懶惰刪除法:當一個元素要被刪除時,它仍留在樹中,只是多了一個刪除的標記。這種方法的優(yōu)點是刪除那一步的時間開銷就可以避免了,如果重新插入刪除的節(jié)點的話,插入時也避免了分配空間的時間開銷。缺點是樹的深度會增加,查找的時間復雜度會增加,插入的時間可能會增加。
刪除函數(shù)代碼如下:
//刪除
template<class T>
void BST<T>::Deletepri(TreeNode<T>* &node,T x)
{
if(node==NULL) return ;//沒有找到值是x的節(jié)點
if(x < node->data)
Deletepri(node->lson,x);//如果x小于節(jié)點的值,就繼續(xù)在節(jié)點的左子樹中刪除x
else if(x > node->data)
Deletepri(node->rson,x);//如果x大于節(jié)點的值,就繼續(xù)在節(jié)點的右子樹中刪除x
else//如果相等,此節(jié)點就是要刪除的節(jié)點
{
if(node->lson&&node->rson)//此節(jié)點有兩個兒子
{
TreeNode<T>* temp=node->rson;//temp指向節(jié)點的右兒子
while(temp->lson!=NULL) temp=temp->lson;//找到右子樹中值最小的節(jié)點
//把右子樹中最小節(jié)點的值賦值給本節(jié)點
node->data=temp->data;
node->freq=temp->freq;
Deletepri(node->rson,temp->data);//刪除右子樹中最小值的節(jié)點
}
else//此節(jié)點有1個或0個兒子
{
TreeNode<T>* temp=node;
if(node->lson==NULL)//有右兒子或者沒有兒子
node=node->rson;
else if(node->rson==NULL)//有左兒子
node=node->lson;
delete(temp);
}
}
return;
}
//刪除接口
template<class T>
void BST<T>::Delete(T x)
{
Deletepri(root,x);
}
第六步:中序遍歷
遍歷的方法和二叉樹的方法一樣,寫這個方法的目的呢,是輸出這個二叉查找樹的有序序列。
代碼如下:
//中序遍歷函數(shù)
template<class T>
void BST<T>::insubtree(TreeNode<T>* node)
{
if(node==NULL) return;
insubtree(node->lson);//先遍歷左子樹
cout<<node->data<<" ";//輸出根節(jié)點
insubtree(node->rson);//再遍歷右子樹
}
//中序遍歷接口
template<class T>
void BST<T>::traversal()
{
insubtree(root);
}
到此,整個代碼就完成了,代碼中肯定有很多不完善的地方請指出,我會加以完善,謝謝。
對于二叉查找樹不穩(wěn)定的時間復雜度的解決方案有不少,平衡二叉樹、伸展樹和紅黑樹都可以解決這個問題,但效果是不一樣的。