CG@CPPBLOG

/*=========================================*/

隨筆 - 76, 文章 - 39, 評論 - 137, 引用 - 0

數據加載中……

我的SICP習題答案（1.14~1.15）

1.14
計算過程的樹如下：

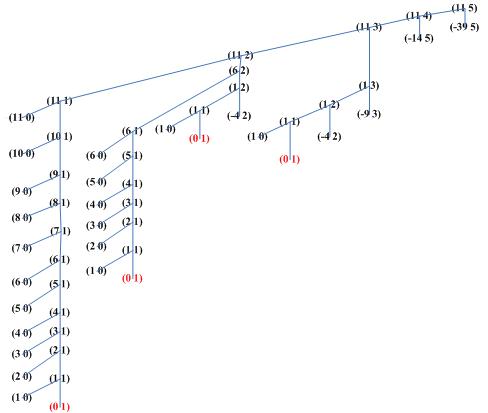
很容易看出，計算過程的空間需求，也就是樹的深度，取決于最左邊的子樹，即(n 1)，它的深度是n+6，O(n).

然后對于計算步數，也就是樹的節點數，我們知道對于一個二叉樹，樹的節點數 = 左子樹節點數 + 右子樹節點數 + 1.
先來看 (n 1) 子樹，設它的節點數是f(n), 而且總有，非葉節點左子樹節點數為1
當 n=1，f(1) = 3
   n>1, f(n) = 1 + f(n-1) + 1 = f(n-1) + 2 = f(n-2) + 2*2
             = f(n-(n-1)) + 2*(n-1) = 2n + 1
             = O(n)

再來看 (n 2) 子樹，設它的節點數 g(n), 設 ┌ n/5 ┐ = A
g(n) = f(n) + g(n-5) + 1 = f(n) + f(n-5) + g(n-5*2) + 2
     = f(n) + ... + f(n-5*(A-1)) + g(n-5*A) + 2A
     = O(n^2)

依此類推，可以得出結論 (n 5) 的計算步數增長的階為 O(n^5)

1.15
a) 12.15 連除 5次 3 小于 0.1 ，所以是 5次
b) 可以看出每調用一次 p 過程，需要遞歸1次 sine ，空間加1，計算步數加2，關鍵是p的次數：
   對于a，調用次數t，那么 a*3^(-t) < 0.1 , 即 10a < 3^t ==> lg(10a)/lg3 < t,
   所以增長階空間和時間都為 O(log a)

posted on 2008-03-26 22:56 cuigang 閱讀(1316) 評論(2) 編輯收藏引用所屬分類: Lisp/Scheme 、我的SICP答案

# re: 我的SICP習題答案（1.14~1.15）回復 更多評論

1.14 題目中是 number of steps used by this process as the amount to be changed increases?
你上面的N是類別把，還是不對哦。。。。。。
以圖上面節點數目為55

2008-07-21 20:12 | xiaokang

# re: 我的SICP習題答案（1.14~1.15）回復 更多評論

@xiaokang

n 是錢數（美分）。

2008-08-03 15:13 | cuigang

刷新評論列表

只有注冊用戶登錄后才能發表評論。
【推薦】100%開源！大型工業跨平臺軟件C++源碼提供，建模，組態！

相關文章: 我的SICP習題答案（2.36~2.39）我的SICP習題答案（2.33~2.35）我的SICP習題答案（2.27~2.32）我的SICP習題答案（2.24~2.26）我的SICP習題答案（2.17~2.23）我的SICP習題答案（2.01~2.08）我的SICP習題答案（1.40~1.44）我的SICP習題答案（1.35~1.39）我的SICP習題答案（1.34）我的SICP習題答案（1.29~1.33）

網站導航: 博客園 IT新聞 BlogJava 博問 Chat2DB 管理

# re: 我的SICP習題答案（1.14~1.15）回復 更多評論

# re: 我的SICP習題答案（1.14~1.15）回復 更多評論

青青草原综合久久大伊人导航_色综合久久天天综合_日日噜噜夜夜狠狠久久丁香五月_热久久这里只有精品

CG@CPPBLOG

我的SICP習題答案（1.14~1.15）

評論

導航

留言簿(5)

隨筆分類(100)

隨筆檔案(76)

文章分類(38)

文章檔案(39)

Others

SICP

Wiki

積分與排名

最新評論

閱讀排行榜

評論排行榜

青青草原综合久久大伊人导航_色综合久久天天综合_日日噜噜夜夜狠狠久久丁香五月_热久久这里只有精品

CG@CPPBLOG

我的SICP習題答案（1.14~1.15）

評論

# re: 我的SICP習題答案（1.14~1.15） 回復 更多評論

# re: 我的SICP習題答案（1.14~1.15） 回復 更多評論

導航

留言簿(5)

隨筆分類(100)

隨筆檔案(76)

文章分類(38)

文章檔案(39)

Others

SICP

Wiki

積分與排名

最新評論

閱讀排行榜

評論排行榜

# re: 我的SICP習題答案（1.14~1.15）回復更多評論

# re: 我的SICP習題答案（1.14~1.15）回復更多評論