這個算法的應用,比如洗牌,這個大家都非常熟悉。很久以前用的是最原始的方法,就是一直rand()未出現的牌,直至生成所有的牌。
這當然是一個while(1)循環,很爛的算法吧。后面聽說直接交換牌,打亂即可了。但是打亂后生成的排列是隨機的么,是等可能隨機的么。
其實,這個問題上算法導論上早已經有了答案了,看過算法導論之后覺得沒看之前真的是算法修養太差了。
算法的偽代碼如下圖所示:

具體c++實現如下:
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
// void Swap(int& nOne, int& nTwo)
// {
// nOne = nOne + nTwo;
// nTwo = nOne - nTwo;
// nOne = nOne - nTwo;
// }
void Swap(int& nOne, int& nTwo)
{
int nTemp;
nTemp = nOne;
nOne = nTwo;
nTwo = nTemp;
}
//返回一個在區間[nBeg, nEnd]內的隨機數
int Random(int nBeg, int nEnd)
{
assert(nEnd >= nBeg);
if (nBeg == nEnd)
{
return nBeg;
}
else
{
return rand() % (nEnd - nBeg + 1) + nBeg;
}
}
void RandomizeInPlace(int* pnA, int nLen)
{
static bool s_bFirst = false;
if (!s_bFirst)
{
srand(time(NULL));
s_bFirst = true;
}
for (int i = 0; i < nLen; ++i)
{
Swap(pnA[i], pnA[Random(i, nLen - 1)]);
}
}
int main()
{
int nArray[20];
int i, j;
for (i = 1; i <= 20; ++i)
{
int nCnt = i;
while (nCnt--)
{
for (j = 0; j < i; ++j)
{
nArray[j] = j;
}
RandomizeInPlace(nArray, i);
for (j = 0; j < i; ++j)
{
printf("%d ", nArray[j]);
}
printf("\n");
}
printf("\n");
}
return 0;
}
運行效果圖片如下:
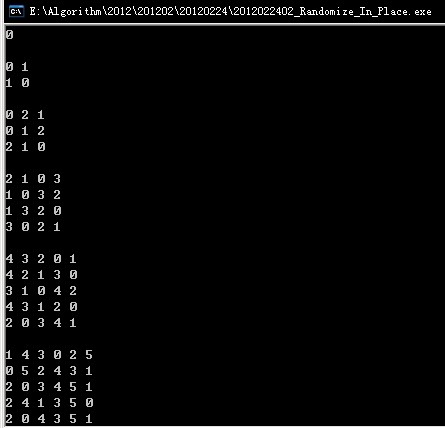
根據運行結果大致就可以感覺到,生成的排列都是隨機的。
這里要多說一句那就是我注釋的那個交換函數其實是有bug的,也許這才是不提倡使用這個交換方法的真正原因,而不僅僅是
難以理解。用同一個變量去調用該函數,會將該變量置0,而不是保持原來的值!!!
至于如何證明這個算法生成的均勻隨機的排列,可以參考算法導論5.3節最后一部分。
證明的大致思路是利用循環不變式的證明方法:證明i次循環后得到某個排列的概論是(n -i)! / n!,那么n次循環后得到最終那個排列的
概論就是1/n!,這樣就證明了該算法能夠得到均勻隨機排列。
這個算法其實就是隨機化算法的一種,其實快排也有所謂的隨機化版本,改動的地方只是隨機選擇了中軸元素而已,這個
在算法導論上也有介紹。