import java.util.Arrays;
/**
* @author Biao
*
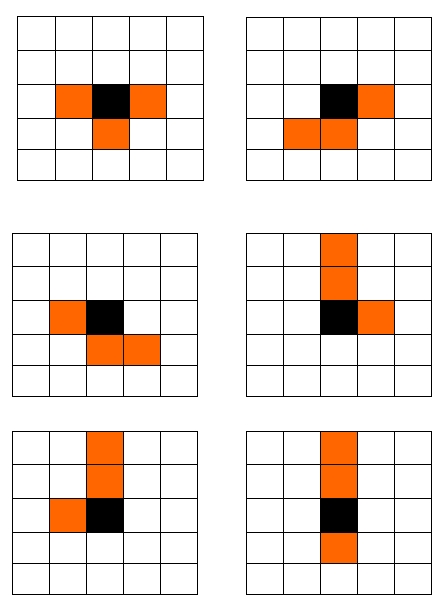
* 在寫俄羅斯方塊時(shí),可以為每個(gè)圖形的每種狀態(tài)都定義一個(gè)數(shù)組來(lái)表示(效率高)。
* 因?yàn)槊總€(gè)圖形有四個(gè)方向的狀態(tài):上右下左,所以每個(gè)圖形要定義四個(gè)數(shù)組來(lái)表示他的狀態(tài)。
* 如果把這些圖形都放在一個(gè)方陣中,圖形的重心為方陣的中心,旋轉(zhuǎn)時(shí)繞方陣中心旋轉(zhuǎn),
* 則圖形的四個(gè)方向的狀態(tài)可以通過旋轉(zhuǎn)方陣來(lái)實(shí)現(xiàn),這樣為每種圖形只需要定義一個(gè)狀態(tài)數(shù)組。
* 而方陣向左或向右旋轉(zhuǎn) 90 度通過算法可以很方便的實(shí)現(xiàn)。
*
* 一般的如圖像旋轉(zhuǎn)任意角度 delta,也是要放在一個(gè)方陣中進(jìn)行處理,以方陣的中心為坐標(biāo)軸原心,
* 然后使用sin, cos計(jì)算出旋轉(zhuǎn)后的坐標(biāo)點(diǎn),取整。
* 如圖像上某一點(diǎn)離原心的距離為 r, 它的角度為 alpha, 逆時(shí)針旋轉(zhuǎn) delta:
* x = r * cos(delta + alpha)
* y = r * sin(delta + alpha)
* 可以把2D坐標(biāo) (x, y) 歸一化,變成(x, y, 1),然后使用上面的公式計(jì)算出旋轉(zhuǎn)矩陣來(lái)計(jì)算更為方便。
*/
public class RotateUtil {
public static enum Direction { LEFT, RIGHT };
/**
* 方陣向右或向左旋轉(zhuǎn)90度。
*/
public static int[][] rotateSquareMatrix(int[][] data, Direction dir) {
int len = data.length;
int last = len - 1;
temp = createTempSquareMatrix(len);
// 代碼量換取計(jì)算效率
if (dir == Direction.LEFT) {
// 向左旋轉(zhuǎn),第一行變第一列,第二行變第二列
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len; ++j) {
temp[last - j][i] = data[i][j];
}
}
} else if (dir == Direction.RIGHT) {
// 向右旋轉(zhuǎn),第一行變第四列,第二行變第n - 2列
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len; ++j) {
temp[j][last - i] = data[i][j];
}
}
}
// 復(fù)制旋轉(zhuǎn)后的數(shù)據(jù)
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len; ++j) {
data[i][j] = temp[i][j];
}
}
return data;
}
public static void printMatrix(int[][] data) {
for (int i = 0; i < data.length; ++i) {
System.out.println(Arrays.toString(data[i]));
}
}
private static int[][] createTempSquareMatrix(int size) {
if (temp == null || temp.length != size) {
temp = new int[size][size];
}
return temp;
}
private static int[][] temp = null;
public static void main(String[] args) {
// 一般的俄羅斯方式 5 * 5 的方陣正好
int[][] data = {
{0, 0, 1, 0, 0},
{0, 0, 1, 0, 0},
{0, 0, 1, 1, 0},
{0, 0, 0, 0, 0},
{0, 0, 0, 0, 0}
};
Direction dir = Direction.LEFT;
String info = "Rotate " + ((dir == Direction.LEFT) ? "left" : "right");
System.out.println("Original Data:");
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println("-------------------------------------------");
dir = Direction.RIGHT;
info = "Rotate " + ((dir == Direction.LEFT) ? "left" : "right");
System.out.println("Original Data:");
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
System.out.println(info);
rotateSquareMatrix(data, dir);
printMatrix(data);
}
}
測(cè)試結(jié)果:
Original Data:
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 1, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
Rotate left
[0, 0, 0, 0, 0]
[0, 0, 1, 0, 0]
[1, 1, 1, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
Rotate left
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 1, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
Rotate left
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 1, 1, 1]
[0, 0, 1, 0, 0]
[0, 0, 0, 0, 0]
Rotate left
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 1, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
-------------------------------------------
Original Data:
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 1, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
Rotate right
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 1, 1, 1]
[0, 0, 1, 0, 0]
[0, 0, 0, 0, 0]
Rotate right
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
[0, 1, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
Rotate right
[0, 0, 0, 0, 0]
[0, 0, 1, 0, 0]
[1, 1, 1, 0, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]
Rotate right
[0, 0, 1, 0, 0]
[0, 0, 1, 0, 0]
[0, 0, 1, 1, 0]
[0, 0, 0, 0, 0]
[0, 0, 0, 0, 0]


