Amber <<Play with Trees Solutions>>
   半徑



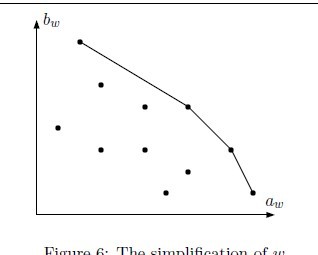
只需計算這些相鄰點Li，即為最優值了

在這之前，需要去除掉一些點，只保留最外層的那些，才能有上面那樣子交點

/*
    n<=200 , m<= 20000的無向圖
    求一棵生成樹，使得任意兩點路徑中的最大值最小

    這題就是求最小直徑生成樹了MSDT
    有Kariv-Hakimi 算法

    Amber的Play with Trees Solutions有這道題比較具體的解答
    
    “最短路徑樹不見得是最小直徑生成樹”
    absoulte center是邊上的一個點（不僅僅是圖的頂點），它也是最短最長路徑的中點
    問題轉化為：
    求absoulte center，使得它到其他頂點最大值（偏心距）最小

    先FLoyd求出任意兩點最短路d[u,v]
    absoulte center必在某條邊，枚舉所有邊u-v
    假設它離u為a，設該點為r，
    f(r) = max{min(d[u,x]+a, w[u,v]-a+d[v,x])}，則為半徑了
    至于確定a，Amber的文章上有比較具體的做法了，其實也就是有Kariv-Hakimi 算法了
    
    覺得比較神奇的是枚舉邊，確定Absolute Center是針對變量a（r離u的距離）作目標的曲線

    timus 1569是邊權為1時的
*/
#include<iostream>
#include<cstring>
#include<map>
#include<algorithm>
#include<stack>
#include<queue>
#include<cstring>
#include<cmath>
#include<string>
#include<cstdlib>
#include<vector>
#include<cstdio>
#include<set>
#include<list>
#include<numeric>
#include<cassert>
#include<sstream>
#include<ctime>
#include<bitset>
#include<functional>

using namespace std;

const int INF = 0x3f3f3f3f;
const int MAXN = 501;

int w[MAXN][MAXN];
int dist[MAXN][MAXN];
int n, m;
int cu, cv;
int pre[MAXN], in[MAXN];
double  dp[MAXN], ans;//為了更準確點。用了double

void update(int u, int v)
{
    vector<pair<int,int> > vt, _vt;
    for (int i = 1; i <= n; i++) {
        vt.push_back(make_pair(dist[u][i], dist[v][i]));
    }
    sort(vt.begin(), vt.end());
    //按照dist[u,i]從小到大排，最后需要考慮點是dist[u,i] < dist[u,j] && dist[v,i] > dist[u,j], i < j
    for (int i = 0; i < vt.size(); i++) {
        while(!_vt.empty() && _vt.back().second <= vt[i].second) {
            _vt.pop_back();
        }
        _vt.push_back(vt[i]);
    }
    int D = INF;//diameter
    double a;
    if (_vt.size() == 1) {
        if (_vt[0].first < _vt[0].second) {
            a = 0;
            D = 2*_vt[0].first;
        } else {
            a = w[u][v];
            D = 2*_vt[0].second;
        }
    }else {
        for (int i = 1; i < _vt.size(); i++) {
            if (D > w[u][v] + _vt[i-1].first + _vt[i].second) {
                a = (w[u][v] + _vt[i].second - _vt[i-1].first) / 2.0;
                D = w[u][v] + _vt[i-1].first + _vt[i].second;
            }
        }
    }
    if (D < ans) {
        cu = u;
        cv = v;
        ans = D;
        dp[u] = a;
        dp[v] = w[u][v] - a;
    }
}

vector<pair<int, int> > edges;

void spfa()
{
    fill(pre+1, pre+1+n, -1);
    fill(in+1, in+1+n, 0);
    for (int i = 1; i <= n; i++) {
        if (i != cu && i != cv) {
            dp[i] = INF;
        }
    }
    in[cu] = in[cv] = 1;
    queue<int> q;
    q.push(cu);
    q.push(cv);
    while (!q.empty()) {
        int t = q.front(); 
        q.pop();
        in[t] = 0;
        for (int i = 1; i <= n; i++) {
            if (w[t][i] != INF && dp[i] > dp[t] + w[t][i]) {
                dp[i] = dp[t]+w[t][i];
                pre[i] = t;
                if (!in[i]) {
                    in[i] = 1;
                    q.push(i);
                }
            }
        }
    }
    edges.clear();
    for (int i = 1; i <= n; i++) {
        if (pre[i] != -1) {
            edges.push_back(make_pair(min(i,pre[i]), max(i,pre[i])));
        }
    }
    if (cv != cu) {
        edges.push_back(make_pair(min(cu,cv), max(cu,cv)));
    }
    return  ;
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in","r",stdin);
#endif
    for (;~scanf("%d%d", &n, &m); ) {
        fill(w[1], w[n+1], INF);
        int a, b, c;
        for (int i = 0; i < m; i++) {
            scanf("%d%d%d", &a, &b, &c);
            w[a][b] = w[b][a] = min(w[a][b], c);
        }
        for (int i = 1; i <= n; i++) {//?
            w[i][i] = 0;
        }
        memcpy(dist, w, sizeof dist);
        for (int k = 1; k <= n; k++) 
            for (int i = 1;  i <= n; i++) 
                if (dist[i][k] != INF) {
                    for (int j = 1; j <= n; j++)
                        dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]);
                }
        ans = INF;
        for (int i = 1; i <= n; i++)
            for (int j = i; j <= n; j++){
                if (w[i][j] != INF) {
                    update(i, j);
                }
            }
        cout<<ans<<endl;
        spfa();
        sort(edges.begin(), edges.end());
        for (vector<pair<int,int> >::iterator it = edges.begin() ; it != edges.end(); it++) {
            printf("%d %d\n", it->first, it->second);
        }
        
    }
    return 0;
}