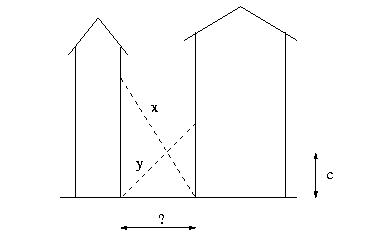
這是個(gè)幾何題目，圖示如下：
?????????2210image.jpg
???????????????????????????????????????????????? ??? (?????? W????? ?)
題目中已知X,Y,C(兩線交點(diǎn)距地面的高度）求街道的寬度(w)。根據(jù)幾何原理求得方程：1/c=1/sqrt((x*x-w*w)+1/sqrt((y*y-w*w))。這是個(gè)不能反解出w的隱方程（我試了很久，都沒做出），所以要計(jì)算w的值就不能那么簡單，所以我們就很快就想到“牛頓迭代法”，但這個(gè)方程的結(jié)構(gòu)比較復(fù)雜（關(guān)鍵是我對(duì)牛頓迭代法不是很了解，呵呵），所以我選用了“二分迭代逼近求值”（我的一位學(xué)姐告訴我的，當(dāng)時(shí)她這道題也沒做，我告訴她這個(gè)公式，怎么樣具體編程時(shí)，告訴我的，由二分搜索引出）。然后我根據(jù)她告訴我的思想做了一個(gè)，代碼如下：

/*
??Name:?二分逼近求解
??Copyright:
??Author:?LonelyTree

??Date:?15-08-08?11:03
??Description:?對(duì)方程w的二分逼近求解：1/c=1/?1/sqrt((x*x-mid*mid))+1/sqrt((y*y-mid*mid))
 */

#include < stdio.h >
#include < math.h >

#define ?EPS?0.000001
int ?main( void )
 {
???? double ?x,y,c;
???? double ?high,low,mid;
???? while (scanf( " %lf?%lf?%lf " , & x, & y, & c) == 3 )
???? {

????????high = x > y ? y:x;
????????low = 0.0 ;
???????? while (high >= low)
???????? {
???????????mid = (high + low) / 2 ;
??????????? if ( 1 / c - 1 / sqrt((x * x - mid * mid)) - 1 / sqrt((y * y - mid * mid)) <= EPS)
??????????? {
????????????????printf( " %.3lf\n " ,mid);
???????????????? break ;
???????????}
??????????? else ? if ( 1 / c - 1 / sqrt((x * x - mid * mid)) - 1 / sqrt((y * y - mid * mid)) > EPS)
??????????? {
????????????????low = mid;
???????????}
??????????? else
??????????? {
???????????????high = mid;
???????????}

????????}
????????

????}
???? return ? 0 ;
}









呵呵，大家看看這段代碼有什么問題。我當(dāng)時(shí)做出了對(duì)提供的4組數(shù)據(jù)進(jìn)行了測(cè)試，OK通過，然后高高興興去sumbit了，令我大吃一驚是個(gè)TLE，哇，心一下就陰了，話了很長時(shí)間做了個(gè)TLE的。然后回過頭來仔細(xì)檢查了一下，經(jīng)幾番思考，對(duì)代碼進(jìn)行如下處理，代碼如下：

/*
??Name:?二分逼近求解
??Copyright:
??Author:?LonelyTree

??Date:?15-08-08?11:03
??Description:?對(duì)方程w的二分逼近求解：1/c=1/?1/sqrt((x*x-mid*mid))+1/sqrt((y*y-mid*mid))
 */

#include < stdio.h >
#include < math.h >

#define ?EPS?0.000001
int ?main( void )
 {
???? double ?x,y,c;
???? double ?high,low,mid;
???? while (scanf( " %lf?%lf?%lf " , & x, & y, & c) == 3 )
???? {

????????high = x > y ? y:x;
????????low = 0.0 ;
???????? while (high - low > EPS)
???????? {
???????????mid = (high + low) / 2 ;
??????????? if ( 1 / c > ( 1 / sqrt((x * x - mid * mid)) + 1 / sqrt((y * y - mid * mid))))
??????????? {
????????????????low = mid;
???????????}
??????????? else
??????????? {
????????????????high = mid;
???????????}

????????}
????????printf( " %.3lf\n " ,mid);

????}
???? return ? 0 ;
}









然后又測(cè)了數(shù)據(jù)，sample過了，然后小心的去sumbit，這次對(duì)了，Accpected了哈！呵呵，現(xiàn)在請(qǐng)大家思考一下這兩種代碼的區(qū)別，為什么前一種是TLE的而后一種是AC的（問題就在while的條件）……