問題描述: 給定n種物品和一背包,物品i的重量是wi,其價值為vi,背包的容量為C。問應如何選擇裝入背包的物品(物品不能分割),使得裝入背包中物品的總價值最大? 抽象描述如下: x[n]:表示物品的選擇,x[i]=1表示選擇放進物品i到背包中。 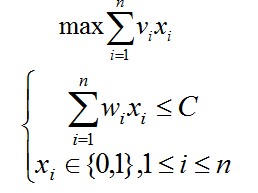 問題分析: 1.抽象之后背包問題轉(zhuǎn)換為找到一個最優(yōu)的數(shù)組,x1,x2,.....,xn的0-1序列。
問題分析: 1.抽象之后背包問題轉(zhuǎn)換為找到一個最優(yōu)的數(shù)組,x1,x2,.....,xn的0-1序列。
2.假設最優(yōu)解的序列為x1,x2,.....,xn,能使背包容量C的總價值最大. 如果,x1=1,則x2,...,xn是C-w1容量的背包的總價值依然是最大的序列; 如果,x1=0,則x2,....,xn是C容量的背包的總價值依然是最大的序列。 這就是我們所說的最優(yōu)子結構性質(zhì)。
3.進一步分析:我們用m(i,j)表示為已經(jīng)判斷好了i:n的序列的背包最大價值,并且此時的背包剩余的容量為j,對物品i進行判斷 如果j>wi, 就只要做出選擇wi和不選擇wi情況下,哪種更能使背包的總價值更大:m(i,j)=max{ m(i+1,j),m(i+1,j-wi)+vi}(注意這是個遞歸式) 如果j<wi: m(i,j)=m(i+1,j) 初始化: m(n,j)=vn (j>= wn); m(n,j)=0 (0<=j< wn) m(0,C)=0 最終的結果:m(1,C) 4.依次我們就得到了一個遞歸的表達式: 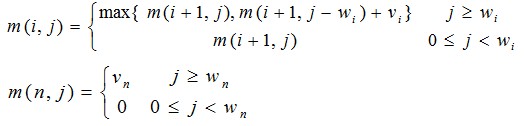
5.如果單純的從利用遞歸,重復計算了很多的值,耗費的時間是很大的,動態(tài)規(guī)劃還需避免這種重復計算,怎樣自頂向下或自底向上的計算呢? 采用列表的方法就可以很好的分析設計自頂向下或自底向上的計算的算法了 舉例分析: n=3,c=6,w={4,3,2} v={5,2,1} m[i][j]=max{ m[i+1][j], m[i+1][j-w[i]]+v[i] } 列表如下: 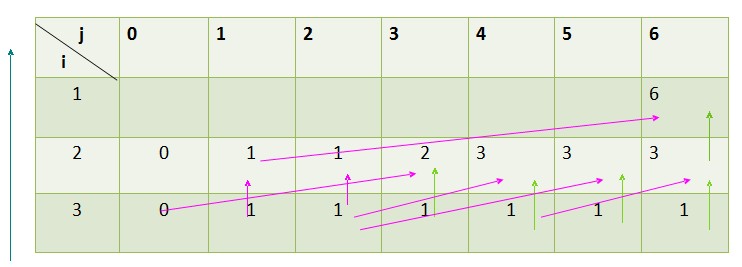 最左邊箭頭:我們計算的方向,從第3行開始向上計算法值。 表中紅色箭頭是我們通過選擇做出的結果:列如 m[2][3]=max{m[3][3],m[3][3-w[2]]+v[2]},我們最終選擇了m[3][3-w[2]]+v[2]。 整個問題的最優(yōu)解保存在m[1][6]中。 代碼實現(xiàn):
最左邊箭頭:我們計算的方向,從第3行開始向上計算法值。 表中紅色箭頭是我們通過選擇做出的結果:列如 m[2][3]=max{m[3][3],m[3][3-w[2]]+v[2]},我們最終選擇了m[3][3-w[2]]+v[2]。 整個問題的最優(yōu)解保存在m[1][6]中。 代碼實現(xiàn):
//w[]:保存物品重量
//v[]:保存物品價值
//n:物品數(shù)目 c:背包容量
//#define max(a,b) (((a) > (b)) ? (a) : (b))
int KnapsackDP(int n,int c)
{
int i,j;
//初始化
for (j=0;j<=c;j++)
{
if (j>=w[n])
m[n][j]=v[n];
else
m[n][j]=0;
}
for (i=n-1;i>=0;i--)
{
for (j=0;j<=c;j++)
{
if (j>=w[i])
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
else
m[i][j]=m[i+1][j];
}
}
return m[1][c];
}
//構造選擇序列x[],x[i]=1表示選擇i號物品放到背包中,則x[i]=0表示不選擇
void Creatx(int x[])
{
for (i=1;i<n;i++)
{
if (m[i][c]==m[i+1][c])
{
x[i]=0;
}
else
{
x[i]=1;
c-=w[i];
}
}
x[n]=m[n][c]?1:0;//m[n][C]==0則表示為沒有選擇第n號物品
}
實戰(zhàn): HDOJ 2602 http://acm.hdu.edu.cn/showproblem.php?pid=2602 
