皮爾遜公式

前言

在很多推薦算法的地方，涉及到了很多關(guān)于數(shù)學(xué)的公式，如果簡(jiǎn)單的應(yīng)用這些公式，那當(dāng)然較為的簡(jiǎn)單，當(dāng)如果有真正的理解這些公式里面隱含著的道理那就要下一定的苦功夫。

我們這里不從皮爾遜的公式講起，我們從物物的推薦開(kāi)始。

問(wèn)題

這里以音樂(lè)的推薦為例子，對(duì)于音樂(lè)的推薦很多人都在做，比較好解釋清楚。給你一首歌曲讓你推薦10首相識(shí)的歌曲。推薦的數(shù)據(jù)來(lái)源是這樣子的。每個(gè)人都會(huì)通過(guò)搜索歌曲來(lái)聽(tīng)他們自己喜歡的歌曲。這樣歌曲就能有一些相關(guān)的特性了，關(guān)于數(shù)據(jù)的問(wèn)題我們等下再進(jìn)一步的說(shuō)明。

如果我們不按數(shù)學(xué)的方法來(lái)思考這個(gè)問(wèn)題的話，平常的人我們會(huì)怎樣來(lái)解決這個(gè)問(wèn)題呢？我們是這樣想的，某一首音樂(lè)，他會(huì)存在不同的用戶中，如果這些用戶也存在著某些歌曲，我們就可以計(jì)算這首歌曲中在不同的用戶中還存在了多少歌曲，這些歌曲的個(gè)數(shù)是多少，就可以有一個(gè)排序，這就是我們要的相識(shí)歌曲。

我們簡(jiǎn)單的用數(shù)學(xué)來(lái)描述一下：

假設(shè)有兩個(gè)人甲，乙，三首歌曲A B C，如果甲有這首歌就標(biāo)記為1，沒(méi)有的話就標(biāo)記為零

   A B C

甲 1 1 1

乙 0 1 0 

按照我們的算法

在甲用戶中

Dict[A][B]=1，Dict[A][C]=1

乙用戶沒(méi)有A

這樣歌曲A和B、C都相識(shí)，而且相識(shí)度都一樣為1。眨眼看上去這種算法，很完美，非常的完美，因?yàn)槠綍r(shí)我們聊起推薦系統(tǒng)的時(shí)候，時(shí)不時(shí)的一開(kāi)口就讓你這樣做了。真的無(wú)懈可擊了當(dāng)然不是這樣，讓我們?cè)倏匆淮螖?shù)據(jù)，你會(huì)發(fā)現(xiàn)，其實(shí)A,C    的數(shù)據(jù)是一樣一樣的，理論上我們會(huì)覺(jué)得A，跟C的相識(shí)度是最高的，但是他的相識(shí)度卻和B一樣，這開(kāi)起來(lái)是不合理的，但這是為什么呢。

改進(jìn)

回想一下如果進(jìn)一步的假設(shè)，用1來(lái)標(biāo)記喜歡，用0來(lái)標(biāo)記不喜歡的話，我們這一種算法其實(shí)是沒(méi)有考慮不喜歡這個(gè)因素的。很多人都認(rèn)為不能這樣假設(shè)，我告訴你，其實(shí)這是數(shù)據(jù)的問(wèn)題，如果我們把使用的數(shù)據(jù)能夠滿足這里的假設(shè)，完全是可以采用的。

這里我想說(shuō)的是，我并不認(rèn)為我們使用的第一個(gè)算法，有多大的問(wèn)題，只是想說(shuō)的是，這種算法還不完美，還可以有改進(jìn)的空間，這不就是我們一直所擁有的理念，把事情改變的更好。

進(jìn)一步的再說(shuō)：如果我們的數(shù)據(jù)不僅是1和0呢，用戶對(duì)歌曲有打分了，怎么辦呢？

  A B C

甲 3 4 3

乙 0 2 0

當(dāng)然很多人會(huì)說(shuō)，算法也可以哦，字典里的數(shù)據(jù)跟著變Dict[A][B]=3，Dict[A][C]=3，但是有個(gè)問(wèn)題不知道有沒(méi)有注意到，每個(gè)人對(duì)打分的理解是不一樣的，有的人覺(jué)得3分就是很好聽(tīng)的歌曲，而有的人要覺(jué)得4分才是很好聽(tīng)的歌曲，也就是說(shuō)，每個(gè)人打分的標(biāo)準(zhǔn)不一樣，導(dǎo)致了打出的分?jǐn)?shù)和比人比較的時(shí)候是不一樣的，但自己的標(biāo)準(zhǔn)大部分的時(shí)間是不會(huì)變的。

皮爾遜公式

這里我們需要一種算法。能夠概括這些情況的。這就是皮爾遜公式。

假設(shè)有兩個(gè)變量X、Y，那么兩變量間的皮爾遜相關(guān)系數(shù)可通過(guò)以下公式計(jì)算：

公式一：

 

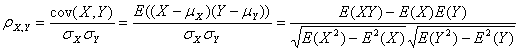
皮爾遜相關(guān)系數(shù)計(jì)算公式

公式二：

 

皮爾遜相關(guān)系數(shù)計(jì)算公式

公式三：

 

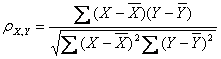
皮爾遜相關(guān)系數(shù)計(jì)算公式

公式四：

 

皮爾遜相關(guān)系數(shù)計(jì)算公式

以上列出的四個(gè)公式等價(jià)，其中E是數(shù)學(xué)期望，cov表示協(xié)方差，N表示變量取值的個(gè)數(shù)。

皮爾遜算法過(guò)于復(fù)雜，如果要有點(diǎn)理解的話，可以使用把維數(shù)降到二維，這樣就跟余弦定理有點(diǎn)相識(shí)了，相識(shí)度就是兩條直線的夾角，角度為0的時(shí)候，皮爾遜的值為1，就是最相識(shí)的，如果角度為180度，代表兩個(gè)牛馬不相干，皮爾遜的值為-1。

總結(jié)

很多時(shí)候，以前牛逼的數(shù)學(xué)家已經(jīng)給了我們很多很好用的數(shù)學(xué)公式，只是如果沒(méi)有真正去用過(guò)的話，我們并不知道他所涉及的原理。好好的研究數(shù)學(xué)公式，他會(huì)給給我們的算法帶來(lái)一定的優(yōu)化作用。關(guān)于公式的優(yōu)化比較難了，以前的數(shù)學(xué)家給了我們很多的想法，而能夠優(yōu)化的就是我們的數(shù)據(jù)，如何取數(shù)據(jù)，這里主要的是，那個(gè)數(shù)據(jù)離用戶的行為越近，離你使用的數(shù)學(xué)模型越近，那個(gè)數(shù)據(jù)就越好用。

參考：

http://lobert.iteye.com/blog/2024999

http://zh.wikipedia.org/wiki/%E7%9A%AE%E5%B0%94%E9%80%8A%E7%A7%AF%E7%9F%A9%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0