題意:
一堆書,每本書都有厚度和高度,管理員試圖將這些書放到三層的書架上,每層都不能為空,求書架最小體積(書架深度顯然為所有書深度最大值,所以與排放方案無關(guān),故取1).
體積公式:
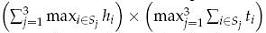
解題思想:
大概思路是DP,這個(gè)要先定下來
設(shè)v=(f(s1)+f(s2)+f(s3))*max{g(s1),g(s2),g(s3)}
其中g(shù)(s3)=SUM-g(s1)-g(s2)
f(s3)=max(h
i)
就說說,我們有4個(gè)決策變量
一個(gè)變量留給DP決策,另一個(gè)變量利用DP狀態(tài)設(shè)計(jì)來消除(這就需要對(duì)初始數(shù)據(jù)排序,保證決策過程中h
i<=h
p2,i屬于s2,p2為當(dāng)前決策點(diǎn))。
這個(gè)問題就轉(zhuǎn)化為在一個(gè)有序隊(duì)列上選擇兩個(gè)分割點(diǎn)p1,p2,h
p1<h
p2,使得max{hi,i屬于s1}<p1,max{hi,i屬于s2}<p2,并且s1,s2,s3均不為空
狀態(tài)可以設(shè)計(jì)為
F(i,t
1,t
2)
即考慮到第i個(gè)元素,s1的總厚度為t1,s2的總厚度為t2時(shí)p1所在元素的高度的最小值。
F(i,t1,t2)=min(F(i-1,t1,t2-data[i].t),data[i].h(當(dāng)F(i-1,t1-data[i].t,t2)合法時(shí)),F(i-1,t1,t2)),顯然,三個(gè)轉(zhuǎn)移意義分別為將當(dāng)前元素分配給s2、s1、s3
當(dāng)F(i,t1,t2)由F(i-1,t1,t2-data[i].t)轉(zhuǎn)移過來的時(shí)候試圖更新全局最優(yōu)解ans=min(ans,(data[i].h+F(i,t1,t2)+data[n-1].h)*t1*t2*(t
total-t1-t2))。注意,這里說F(i,t1,t2)由F(i-1,t1,t2-data[i].t)轉(zhuǎn)移過來指的是F(i-1,t1,t2-data[i].t)<=min(data[i].h(當(dāng)F(i-1,t1-data[i].t,t2)合法時(shí)),F(i-1,t1,t2)),等于不能丟掉(原因?只有此時(shí)才能更新全局最優(yōu)解)
代碼如下


1 Source Code
2
3 Problem: 3124 User: yzhw
4 Memory: 17744K Time: 2188MS
5 Language: G++ Result: Accepted
6 Source Code
7 # include <cstdio>
8 # include <utility>
9 # include <functional>
10 # include <cstring>
11 # include <vector>
12 # include <algorithm>
13 using namespace std;
14 # define M 2105
15 # define N 100
16 int dp[M][M],n,total,ans,sum[N];
17 pair<int,int> data[N];
18 bool cmp(const pair<int,int> &a,const pair<int,int> &b)
19 {
20 return a.first<b.first;
21 }
22
23 int main()
24 {
25 //freopen("bookcase.in","r",stdin);
26 int test;
27 scanf("%d",&test);
28 for(int t=1;t<=test;t++)
29 {
30 scanf("%d",&n);
31 total=0;
32 ans=0xfffffff;
33 for(int i=1;i<=n;i++)
34 {
35 scanf("%d%d",&data[i].first,&data[i].second);
36 total+=data[i].second;
37 }
38 sort(data+1,data+n+1,cmp);
39 sum[0]=0;
40 for(int i=1;i<=n;i++)
41 sum[i]=sum[i-1]+data[i].second;
42 memset(dp,-1,sizeof(dp));
43 dp[0][0]=0;
44 for(int i=1;i<=n;i++)
45 {
46 for(int j=sum[i-1];j>=0;j--)
47 for(int k=sum[i-1];k>=0;k--)
48 if(dp[j][k]!=-1)
49 {
50 if(dp[j+data[i].second][k]==-1||dp[j+data[i].second][k]>data[i].first)
51 dp[j+data[i].second][k]=data[i].first;
52 if(dp[j][k+data[i].second]==-1||dp[j][k+data[i].second]>=dp[j][k])
53 {
54 dp[j][k+data[i].second]=dp[j][k];
55 if(j&&j+k+data[i].second!=total)
56 ans=min(ans,(dp[j][k]+data[i].first+data[n].first)*max(j,max(k+data[i].second,total-j-k-data[i].second)));
57 }
58 }
59 }
60 printf("%d\n",ans);
61
62 }
63 return 0;
64
65