題意:
N個(gè)任務(wù)，每個(gè)任務(wù)有兩個(gè)參數(shù)，完成需要的時(shí)間t以及因子f，現(xiàn)在將這些任務(wù)分組，加工每個(gè)分組前機(jī)器需要冷卻時(shí)間start，完成一組任務(wù)耗時(shí)為 t + Start + (Tx + Tx+1 + ... + Tx+k)，問最少耗費(fèi)的時(shí)間。
解法：
首先先解決這個(gè)問題，在這種分組數(shù)不確定的問題中，根據(jù)背包九講中無限背包的策略，外層循環(huán)只要一層即可完成。
關(guān)鍵是內(nèi)重循環(huán)還要枚舉本組的起始位置，如果暴力的做就要N2了。
下面試圖對(duì)初始的DP方程進(jìn)行優(yōu)化
考慮兩種規(guī)劃方向，第一種規(guī)劃方向是從前到后
dp[i]=min{dp[k]+(dp[k]+sumt(i)-sumt(k)+start)*(sumf(i)-sumf(k))} 無比復(fù)雜的一個(gè)式子，推了N小時(shí)，在這個(gè)式子上下手似乎非常困難。。。（3個(gè)決策變量）
但是，如果換種思路，從后向前，將sumt以及sumf重新定義為最后一個(gè)任務(wù)到第i個(gè)任務(wù)的時(shí)間和和參數(shù)和，這樣就簡(jiǎn)單多了。
dp[i]=min{dp[k]+(sumt(i)-sumt(k)+start)*sumf(i)}
然后很輕易能發(fā)現(xiàn)這個(gè)滿足斜率優(yōu)化的條件（2個(gè)待定決策變量，sumt(k)和dp(k)）。
關(guān)于斜率優(yōu)化，一般有代數(shù)和幾何兩種方法。先說幾何方法
令g=dp[k]+(sumt(i)-sumt(k)+start)*sumf(i)}，y=dp[k],x=sumt[k]
現(xiàn)在要使g最小
將式子整理下
y=sumf(i)*x+f-(start+sumt(i))*sumf(i)
將這個(gè)看做一個(gè)線性函數(shù)，目標(biāo)要使得截距最小
再觀察一下，斜率sumf(i)恒為正，且是隨著i單調(diào)遞減的，換句話說，是隨著規(guī)劃的過程單調(diào)遞增的，而自變量x也是隨著規(guī)劃的過程單調(diào)遞增的。我們畫個(gè)圖比劃下
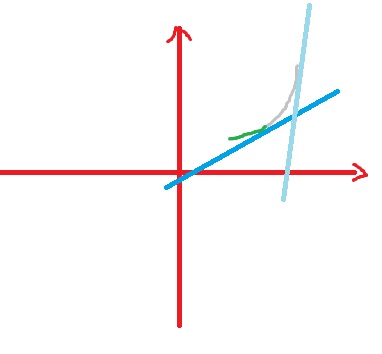
首先，我們要維護(hù)的是一個(gè)上凹線，因?yàn)榘季€內(nèi)部的點(diǎn)不會(huì)被斜率為正的直線切到。再者，我們發(fā)現(xiàn)最優(yōu)決策就在凹線的左端。我們來觀察藍(lán)色的線，假設(shè)這個(gè)是第i階段的決策線，灰色凹線與藍(lán)色線切點(diǎn)左側(cè)的綠色部分顯然是可以丟棄的。應(yīng)為在切點(diǎn)處截距達(dá)到最小。并且在以后的決策中（淺藍(lán)色的線），該段同樣不會(huì)有任何作用。根據(jù)以上觀察，我們可以使用棧隊(duì)列（很多人簡(jiǎn)稱為單調(diào)隊(duì)列）的數(shù)據(jù)結(jié)構(gòu)。這個(gè)東西網(wǎng)上介紹的比較多，我就不細(xì)說了。
第二種方法就是代數(shù)法。
我看網(wǎng)上有一個(gè)牛寫的不錯(cuò)，就貼過來吧- -
初始化的時(shí)候要注意，
必須在n+1的位置處加一個(gè)虛擬的狀態(tài)，不能將第一個(gè)狀態(tài)（即i=n的狀態(tài)）作為初始狀態(tài)，因?yàn)榭赡軐⑺腥蝿?wù)僅分為一段。
代碼：
1
# include <stdio.h>
2# define N 10005
3int n,start,st[N],sf[N];
4int q[N],s=-1,e=0;
5int dp[N];
6int cmp(const int a,const int b,const int k)
7
{
8
if(dp[b]-dp[a]<(long long)k*(st[b]-st[a])) return -1;
9 else if((long long)dp[b]-dp[a]==(long long)k*(st[b]-st[a])) return 0;
10 else return 1;
11
}
12int cmp1(const int y1,const int x1,const int y2,const int x2,const int y3,const int x3)
13{
14 if(((long long)y3-y2)*(x2-x1)<((long long)y2-y1)*(x3-x2)) return -1;
15 else if(((long long)y3-y2)*(x2-x1)==((long long)y2-y1)*(x3-x2)) return 0;
16 else return 1;
17}
18int main()
19{
20 int i;
21 scanf("%d%d",&n,&start);
22 for(i=0;i<n;i++)
23 scanf("%d%d",st+i,sf+i);
24 for(i=n-2;i>=0;i--)
25
{
26 st[i]+=st[i+1];
27 sf[i]+=sf[i+1];
28
}
29 q[e]=n;
30 dp[n]=0;
31 for(i=n-1;i>=0;i--)
32 {
33 while(e>=s+2&&cmp(q[s+1],q[s+2],sf[i])!=1) s++;
34 dp[i]=dp[q[s+1]]+(start+st[i]-st[q[s+1]])*sf[i];
35 while(e>=s+2&&cmp1(dp[q[e-1]],st[q[e-1]],dp[q[e]],st[q[e]],dp[i],st[i])!=1) e--;
36 q[++e]=i;
37 }
38 printf("%d\n",dp[0]);
39 return 0;
40}
41