簡明題意：給出一個城市的道路網(wǎng)(是一棵樹)，每條路有一定的權(quán)值，一個人在第k點，給出一些城市列表，問這個人游覽完這些城市最小花費為多少
解法：一條最優(yōu)的路線肯定是這樣
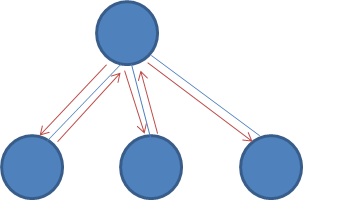
有且僅有一條路線是單向的。
下面定義狀態(tài):
dp[i][0]為游覽完以i為根節(jié)點的子樹（僅僅游覽需要游覽的城市，如果沒有即為0）且最后回到i節(jié)點需要的最短長度
dp[i][1]為不需要回到i節(jié)點的最短長度
dp[i][0]=sum(dp[j][0]+val[i][j](如果dp[j][0]不為0或者j為需要訪問的城市)),j為i的孩子節(jié)點
dp[i][1]=dp[i][0]-max(dp[j][0]-dp[j][1]+val[i][j](如果dp[j][0]不為0或者j為需要訪問的城市))
最后結(jié)果就是dp[start][1]
程序如下
1
# include <cstdio>
2# include <cstring>
3# include <vector>
4//# include <algorithm>
5using namespace std;
6# define max(a,b) ((a)>(b)?(a):(b))
7int dp[50001][2];
8bool need[50001];
9int g[50001],nxt[100005],val[100005],v[100005],c=0;
10inline void insert(int a,int b,int p)
11
{
12
v[c]=b;
13 val[c]=p;
14 nxt[c]=g[a];
15 g[a]=c++;
16
}
17void solve(int pos,int pre)
18{
19 int maxnum=0;
20 dp[pos][0]=dp[pos][1]=0;
21 for(int p=g[pos];p!=-1;p=nxt[p])
22 if(v[p]!=pre)
23
{
24 solve(v[p],pos);
25 maxnum=max(dp[v[p]][0]-dp[v[p]][1]+(dp[v[p]][0]||need[v[p]]?val[p]:0),maxnum);
26 dp[pos][0]+=dp[v[p]][0]+(dp[v[p]][0]||need[v[p]]?2*val[p]:0);
27
}
28 dp[pos][1]=dp[pos][0]-maxnum;
29}
30int main()
31{
32 int n,start,num;
33 scanf("%d%d",&n,&start);
34 memset(g,-1,sizeof(g));
35 memset(need,false,sizeof(need));
36 memset(dp,-1,sizeof(dp));
37 for(int i=1;i<n;i++)
38 {
39 int a,b,p;
40 scanf("%d%d%d",&a,&b,&p);
41 insert(a,b,p);
42 insert(b,a,p);
43 }
44 scanf("%d",&num);
45 while(num--)
46 {
47 int t;
48 scanf("%d",&t);
49 need[t]=true;
50 }
51 solve(start,-1);
52 printf("%d\n",dp[start][1]);
53 // system("pause");
54 return 0;
55}
56
57