【題意】:有 M 個豬圈(M ≤ 1000),每個豬圈里初始時有若干頭豬。開始所有豬圈都是關閉的。依次來了 N 個顧客(N ≤ 100),每個顧客分別會打開指定的幾個豬圈,從中買若干頭豬。每個顧客分別都有他能夠買的數量的上限。每個顧客走后,他打開的那些豬圈中的豬,都可以被任意地調換到其它開著的豬圈里,然后所有豬圈重新關上。 問總共最多能賣出多少頭豬。
【題解】:舉個例子來說。有 3 個豬圈,初始時分別有 3、 1 和 10 頭豬。依次來了 3 個顧客,第一個打開 1 號 和 2 號豬圈,最多買 2 頭;第二個打開 1 號 和 3 號豬圈,最多買 3 頭;第三個打開 2 號豬圈,最多買 6 頭。那么,最好的可能性之一就是第一個顧客從 1 號圈買 2 頭,然后把 1 號圈剩下的 1 頭放到 2 號圈;第二個顧客從 3 號圈買 3 頭;第三個顧客從 2 號圈買 2 頭。總共賣出 2 + 3 + 2 = 7 頭。□
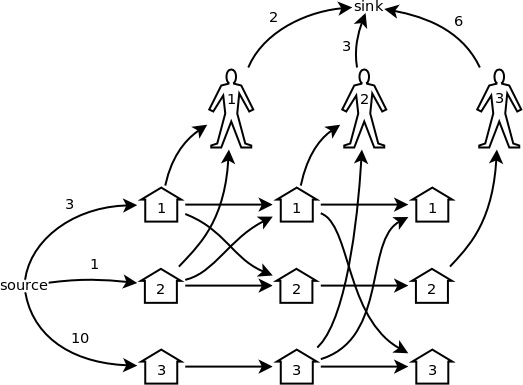
不難想像,這個問題的網絡模型可以很直觀地構造出來。就拿上面的例子來說,可以構造出圖1所示的模型(圖中凡是沒有標數字的邊,容量都是 +∞):
不難想像,這個網絡模型的最大流量就是最多能賣出的數量。圖中最多有 2 + N + M × N ≈ 100,000 個節點。□
這個模型雖然很直觀,但是節點數太多了,計算速度肯定會很慢。其實不用再想別的算法,就讓我們繼續上面的例子,用合并的方法來簡化這個網絡模型。
首先,最后一輪中沒有打開的豬圈就可以從圖中刪掉了,也就是中圖2紅色的部分,顯然它們對整個網絡的流量沒有任何影響。
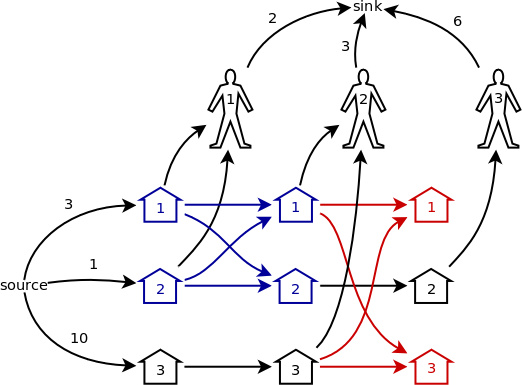
圖 2
接著,看圖 2 中藍色的部分。根據我總結出的以下幾個規律,可以把這 4 個點合并成一個:
規律 1. 如果幾個節點的流量的來源完全相同,則可以把它們合并成一個。
規律 2. 如果幾個節點的流量的去向完全相同,則可以把它們合并成一個。
規律 3. 如果從點 u 到點 v 有一條容量為 +∞ 的邊,并且 u 是 v 的唯一流量來源,或者 v 是 u 的唯一流量去向,則可以把 u 和 v 合并成一個節點。
根據規律1,可以把藍色部分右邊的 1、 2 號節點合并成一個;根據規律2,可以把藍色部分左邊的 1、 2 號節點合并成一個;最后,根據規律3,可以把藍色部分的左邊和右邊(已經分別合并成了一個節點)合并成一個節點。于是,圖2被簡化成了圖3的樣子。也就是說,最后一輪除外,每一輪被打開的豬圈和下一輪的同樣這些豬圈都可以被合并成一個點。
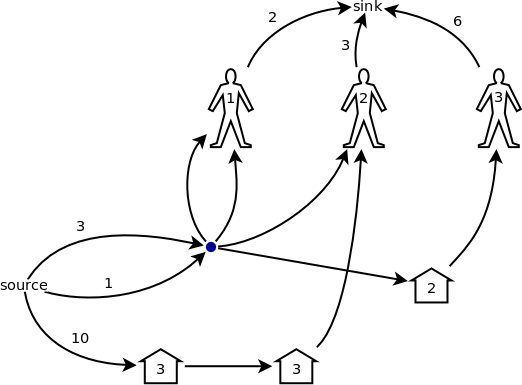
圖 3
讓我們從圖4中重新總結一下構造這個網絡模型的規則:
新的網絡模型中最多只有 2 + N = 102 個節點,計算速度就可以相當快了。可以這樣理解這個新的網絡模型:對于某一個顧客,如果他打開了豬圈 h,則在他走后,他打開的所有豬圈里剩下的豬都有可能被換到 h 中,因而這些豬都有可能被 h 的下一個顧客買走。所以對于一個顧客打開的所有豬圈,從該顧客到各豬圈的下一個顧客,都要連一條容量為 +∞ 的邊。
在面對網絡流問題時,如果一時想不出很好的構圖方法,不如先構造一個最直觀,或者說最“硬來”的模型,然后再用合并節點和邊的方法來簡直化這個模型。經過簡化以后,好的構圖思路自然就會涌現出來了。這是解決網絡流問題的一個好方法。
【代碼】:
【題解】:舉個例子來說。有 3 個豬圈,初始時分別有 3、 1 和 10 頭豬。依次來了 3 個顧客,第一個打開 1 號 和 2 號豬圈,最多買 2 頭;第二個打開 1 號 和 3 號豬圈,最多買 3 頭;第三個打開 2 號豬圈,最多買 6 頭。那么,最好的可能性之一就是第一個顧客從 1 號圈買 2 頭,然后把 1 號圈剩下的 1 頭放到 2 號圈;第二個顧客從 3 號圈買 3 頭;第三個顧客從 2 號圈買 2 頭。總共賣出 2 + 3 + 2 = 7 頭。□
不難想像,這個問題的網絡模型可以很直觀地構造出來。就拿上面的例子來說,可以構造出圖1所示的模型(圖中凡是沒有標數字的邊,容量都是 +∞):
- 三個顧客,就有三輪交易,每一輪分別都有 3 個豬圈和 1 個顧客的節點。
- 從源點到第一輪的各個豬圈各有一條邊,容量就是各個豬圈里的豬的初始數量。
- 從各個顧客到匯點各有一條邊,容量就是各個顧客能買的數量上限。
- 在某一輪中,從該顧客打開的所有豬圈都有一條邊連向該顧客,容量都是 +∞。
- 最后一輪除外,從每一輪的 i 號豬圈都有一條邊連向下一輪的 i 號豬圈,容量都是 +∞,表示這一輪剩下的豬可以留到下一輪。
- 最后一輪除外,從每一輪被打開的所有豬圈,到下一輪的同樣這些豬圈,兩兩之間都要連一條邊,表示它們之間可以任意流通。

圖 1
不難想像,這個網絡模型的最大流量就是最多能賣出的數量。圖中最多有 2 + N + M × N ≈ 100,000 個節點。□
這個模型雖然很直觀,但是節點數太多了,計算速度肯定會很慢。其實不用再想別的算法,就讓我們繼續上面的例子,用合并的方法來簡化這個網絡模型。
首先,最后一輪中沒有打開的豬圈就可以從圖中刪掉了,也就是中圖2紅色的部分,顯然它們對整個網絡的流量沒有任何影響。

圖 2
接著,看圖 2 中藍色的部分。根據我總結出的以下幾個規律,可以把這 4 個點合并成一個:
規律 1. 如果幾個節點的流量的來源完全相同,則可以把它們合并成一個。
規律 2. 如果幾個節點的流量的去向完全相同,則可以把它們合并成一個。
規律 3. 如果從點 u 到點 v 有一條容量為 +∞ 的邊,并且 u 是 v 的唯一流量來源,或者 v 是 u 的唯一流量去向,則可以把 u 和 v 合并成一個節點。
根據規律1,可以把藍色部分右邊的 1、 2 號節點合并成一個;根據規律2,可以把藍色部分左邊的 1、 2 號節點合并成一個;最后,根據規律3,可以把藍色部分的左邊和右邊(已經分別合并成了一個節點)合并成一個節點。于是,圖2被簡化成了圖3的樣子。也就是說,最后一輪除外,每一輪被打開的豬圈和下一輪的同樣這些豬圈都可以被合并成一個點。

圖 3
接著,根據,圖3中的藍色節點、2 號豬圈和 1 號顧客這三點可以合并成一個;圖3中的兩個 3 號豬圈和 2 號顧客也可以合并成一個點。當然,如果兩點之間有多條同向的邊,則這些邊可以合并成一條,容量相加,這個道理很簡單,就不用我多說了。最終,上例中的網絡模型被簡化成了圖4 的樣子。
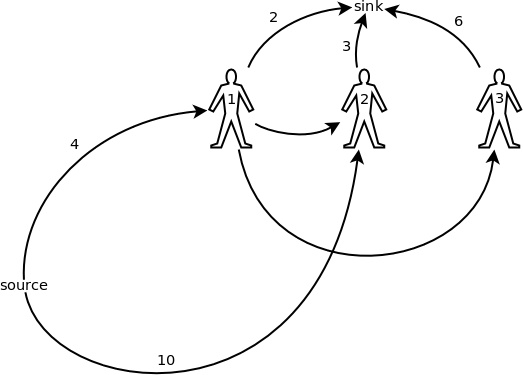
圖 4
讓我們從圖4中重新總結一下構造這個網絡模型的規則:
- 每個顧客分別用一個節點來表示。
- 對于每個豬圈的第一個顧客,從源點向他連一條邊,容量就是該豬圈里的豬的初始數量。如果從源點到一名顧客有多條邊,則可以把它們合并成一條,容量相加。
- 對于每個豬圈,假設有 n 個顧客打開過它,則對所有整數 i ∈ [1, n),從該豬圈的第 i 個顧客向第 i + 1 個顧客連一條邊,容量為 +∞。
- 從各個顧客到匯點各有一條邊,容量是各個顧客能買的數量上限。
新的網絡模型中最多只有 2 + N = 102 個節點,計算速度就可以相當快了。可以這樣理解這個新的網絡模型:對于某一個顧客,如果他打開了豬圈 h,則在他走后,他打開的所有豬圈里剩下的豬都有可能被換到 h 中,因而這些豬都有可能被 h 的下一個顧客買走。所以對于一個顧客打開的所有豬圈,從該顧客到各豬圈的下一個顧客,都要連一條容量為 +∞ 的邊。
在面對網絡流問題時,如果一時想不出很好的構圖方法,不如先構造一個最直觀,或者說最“硬來”的模型,然后再用合并節點和邊的方法來簡直化這個模型。經過簡化以后,好的構圖思路自然就會涌現出來了。這是解決網絡流問題的一個好方法。
【代碼】:
1 #include "iostream"
2 using namespace std;
3 #define maxn 500
4 #define maxm 50005
5 #define maxhouse 1005
6 const int INF = 99999999;
7 int s, t, house, ctm, tot;
8 int eh[maxn], pre[maxn], cur[maxn], gap[maxn], dist[maxn], a[maxn], hcap[maxhouse];
9 bool visit[maxhouse];
10
11 struct Edge {
12 int u, v, cap, flow, next;
13 }et[maxm];
14
15 void init() {
16 tot = 0;
17 memset(eh, -1, sizeof(eh));
18 }
19
20 int min(int a, int b) {
21 return a < b ? a : b;
22 }
23
24 void add(int u, int v, int cap, int flow) {
25 Edge E = {u, v, cap, flow, eh[u]};
26 et[tot] = E;
27 eh[u] = tot++;
28 }
29
30 void addedge(int u, int v, int cap) {
31 add(u, v, cap, 0), add(v, u, 0, 0);
32 }
33
34 int isap(int s, int t, int n) {
35 int u, v, now;
36 memset(dist, 0, sizeof(dist));
37 memset(a, 0, sizeof(a));
38 for(u = 0; u <= n; u++) cur[u] = eh[u];
39 int maxflow = 0;
40 u = s, a[s] = INF, gap[0] = n;
41 while(dist[s] < n) {
42 for(now = cur[u]; now != -1; now = et[now].next)
43 if(et[now].cap - et[now].flow && dist[u] == dist[v = et[now].v] + 1)
44 break;
45 if(now != -1) {
46 cur[u] = pre[v] = now;
47 a[v] = min(a[u], et[now].cap - et[now].flow);
48 u = v;
49 if(u == t) {
50 for(; u != s; u = et[pre[u]].u) {
51 et[pre[u]].flow += a[t];
52 et[pre[u]^1].flow -= a[t];
53 }
54 maxflow += a[t], a[s] = INF;
55 }
56 } else {
57 if(--gap[dist[u]] == 0) break;
58 dist[u] = n;
59 cur[u] = eh[u];
60 for(now = eh[u]; now != -1; now = et[now].next)
61 if(et[now].cap - et[now].flow && dist[u] > dist[et[now].v] + 1)
62 dist[u] = dist[et[now].v] + 1;
63 gap[dist[u]]++;
64 if(u != s) u = et[pre[u]].u;
65 }
66 }
67 return maxflow;
68 }
69
70 int main() {
71 int i, j, cap, v, nkey;
72 memset(visit, false, sizeof(visit));
73 cin >> house >> ctm;
74 init();
75 s = 0, t = ctm + 1;
76 for(i = 1; i <= house; i++) {
77 cin >> hcap[i];
78 }
79 for(i = 1; i <= ctm; i++) {
80 cin >> nkey;
81 for(j = 1; j <= nkey; j++) {
82 cin >> v;
83 if(!visit[v]) {
84 addedge(s, i, hcap[v]);
85 visit[v] = true;
86 pre[v] = i;
87 }
88 else addedge(pre[v], i, INF);
89 }
90 cin >> cap;
91 addedge(i, t, cap);
92 }
93 cout << isap(s, t, t - s + 1) << endl;
94 return 0;
95 }
2 using namespace std;
3 #define maxn 500
4 #define maxm 50005
5 #define maxhouse 1005
6 const int INF = 99999999;
7 int s, t, house, ctm, tot;
8 int eh[maxn], pre[maxn], cur[maxn], gap[maxn], dist[maxn], a[maxn], hcap[maxhouse];
9 bool visit[maxhouse];
10
11 struct Edge {
12 int u, v, cap, flow, next;
13 }et[maxm];
14
15 void init() {
16 tot = 0;
17 memset(eh, -1, sizeof(eh));
18 }
19
20 int min(int a, int b) {
21 return a < b ? a : b;
22 }
23
24 void add(int u, int v, int cap, int flow) {
25 Edge E = {u, v, cap, flow, eh[u]};
26 et[tot] = E;
27 eh[u] = tot++;
28 }
29
30 void addedge(int u, int v, int cap) {
31 add(u, v, cap, 0), add(v, u, 0, 0);
32 }
33
34 int isap(int s, int t, int n) {
35 int u, v, now;
36 memset(dist, 0, sizeof(dist));
37 memset(a, 0, sizeof(a));
38 for(u = 0; u <= n; u++) cur[u] = eh[u];
39 int maxflow = 0;
40 u = s, a[s] = INF, gap[0] = n;
41 while(dist[s] < n) {
42 for(now = cur[u]; now != -1; now = et[now].next)
43 if(et[now].cap - et[now].flow && dist[u] == dist[v = et[now].v] + 1)
44 break;
45 if(now != -1) {
46 cur[u] = pre[v] = now;
47 a[v] = min(a[u], et[now].cap - et[now].flow);
48 u = v;
49 if(u == t) {
50 for(; u != s; u = et[pre[u]].u) {
51 et[pre[u]].flow += a[t];
52 et[pre[u]^1].flow -= a[t];
53 }
54 maxflow += a[t], a[s] = INF;
55 }
56 } else {
57 if(--gap[dist[u]] == 0) break;
58 dist[u] = n;
59 cur[u] = eh[u];
60 for(now = eh[u]; now != -1; now = et[now].next)
61 if(et[now].cap - et[now].flow && dist[u] > dist[et[now].v] + 1)
62 dist[u] = dist[et[now].v] + 1;
63 gap[dist[u]]++;
64 if(u != s) u = et[pre[u]].u;
65 }
66 }
67 return maxflow;
68 }
69
70 int main() {
71 int i, j, cap, v, nkey;
72 memset(visit, false, sizeof(visit));
73 cin >> house >> ctm;
74 init();
75 s = 0, t = ctm + 1;
76 for(i = 1; i <= house; i++) {
77 cin >> hcap[i];
78 }
79 for(i = 1; i <= ctm; i++) {
80 cin >> nkey;
81 for(j = 1; j <= nkey; j++) {
82 cin >> v;
83 if(!visit[v]) {
84 addedge(s, i, hcap[v]);
85 visit[v] = true;
86 pre[v] = i;
87 }
88 else addedge(pre[v], i, INF);
89 }
90 cin >> cap;
91 addedge(i, t, cap);
92 }
93 cout << isap(s, t, t - s + 1) << endl;
94 return 0;
95 }


