|
|
這是我們操作系統的大作業。 原理就是inline hook 那個 proc 文件系統，根目錄下的 readdir 的函數。 替換掉第三個參數，filldir。 代碼爆短，60來行。 Ubuntu 10.04 測試可用。
 #include <linux/kernel.h>
#include <linux/kprobes.h>
#include <linux/module.h>
#include <linux/moduleparam.h>
#include <linux/fs.h>
int register_kprobe(struct kprobe *kp);
  static struct kprobe kp =  {
 .symbol_name = "proc_pid_readdir",
 };
static filldir_t old_filldir;
static int pid;
module_param(pid, int, 0744);
static int filldir(void * __buf, const char * name, int namlen, loff_t offset,
u64 ino, unsigned int d_type)
{
int p;
sscanf(name, "%d", &p);
if (p == pid)
return 0;
return old_filldir(__buf, name, namlen, offset, ino, d_type);
}
/**//* kprobe pre_handler: called just before the probed instruction is executed */
static int handler_pre(struct kprobe *pr, struct pt_regs *regs)
{
old_filldir = (filldir_t)regs->cx;
regs->cx = (typeof(regs->cx))filldir;
return 0;
}
static int __init k_init(void)
{
int ret;
kp.pre_handler = handler_pre;
ret = register_kprobe(&kp);
  if (ret < 0) {
printk(KERN_INFO "register_kprobe failed, returned %d\n", ret);
return ret;
 }
printk(KERN_INFO "Planted kprobe at %p; pid %d\n", kp.addr, pid);
return 0;
}
static void __exit k_exit(void)
{
unregister_kprobe(&kp);
printk(KERN_INFO "kprobe at %p unregistered\n", kp.addr);
}
module_init(k_init);
module_exit(k_exit);
MODULE_LICENSE("GPL");
sleep 1000 &
pid=`jobs -p`
echo 'before hide'
ps aux | grep $pid
insmod k.ko pid=$pid
echo 'after hide'
ps aux | grep $pid
rmmod k.ko
echo 'after unhide'
ps aux | grep $pid
可以看出，達到最大size的時候一定是某個蛋糕剛好被分完，如果再大一點的話，肯定就不能解決了。
比這個size小，則無論如何都可以解決。
所以可以通過二分答案的方法來解決這個問題。就很簡單了。 注意：這題精度要求很高，pi的值需要通過acos(-1)來求，eps要到e-5。 我用C++提交能夠AC，g++一直WA。 嗎的，數據能不能寬容點。
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
int N, F;
double pi = acos(-1.0);
double pie[10032];
double sum, maxp;
int main()
{
double l, r, m;
int i, t, c;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &N, &F);
F++;
maxp = sum = 0;
for (i = 0; i < N; i++) {
scanf("%d", &c);
pie[i] = c*c*pi;
maxp = max(maxp, pie[i]);
sum += pie[i];
}
l = maxp / F;
r = sum / F;
while (l + 0.00001 < r) {
m = (l + r) / 2;
c = 0;
for (i = 0; i < N; i++)
c += floor(pie[i] / m);
if (c < F)
r = m;
else
l = m;
}
printf("%.4lf\n", l);
}
return 0;
}
摘要: 可以開一個閉hash表。棧里面存放的只是hash表的下標。這樣比較兩個set是否一樣，就只需要比較他們的下標是否一樣。同時對每個set，要保存它的孩子，一樣存放的是hash表的下標。
union和intersect操作，如果是按序存放孩子的話，復雜度可以低至O(N)。空間復雜度為O(N^2)。
#include <stdio.h>#include <str... 閱讀全文
摘要: 題目大意：給出一個已經完成的數獨，和一個未完成的數獨。判斷前者能否經過演化后成為后者的解。演化的操作有：1）改變數字1～9的映射2）旋轉數獨3）交換3x9中的行或列4）交換兩個3x9解法：實際上就是常規的搜索，不過代碼難寫點。4）中共有6*6種情況3）中共有(6*6*6)*(6*6*6)種情況在搜索3）的時候，首先固定列，然后枚舉行，這樣就可以節省一些時間。我的代碼 250ms
Code hig... 閱讀全文
題目的意思是： 給一個有n個點，m條邊的無向圖 兩點之間可以存在多條邊 現在每次隨機增加一條邊 問使得全部點都連通需要增加多少次（期望值） 首先，求出所有連通分量。用并查集。 每次隨機增加一條邊的時候一共有兩種情況： 1）這條邊連接了兩個不同的連通分量，它的概率是p 2）這條邊在一個連通分量里，它的概率是q = 1 - p 前者可以改變連通分量的數量，后者不能 如果把當前圖的狀態視為一個子問題 那么就可以用動態規劃解決問題了 圖的狀態可以表示為：有多少個連通分量，每個連通分量包含多少個點
比如說圖的狀態 (2, 3, 3) 表示有三個連通分量，每個連通分量包含的點的個數分別為 2, 3, 3 動態規劃的轉移方程為： f = p*(1+r) + p*q*(2+r) + p*q^2*(3+r) .... 其中r為p發生后，新狀態的期望值 這個東西高中的時候學過，呵呵。 而1）中也包含多種情況，需要兩兩枚舉 最大的問題是，f的值是一個無限數列，它的極值很難求。但無論如何，有高手求出來了。。在這里：http://archive.cnblogs.com/a/1325929/
它的極值是 f = p * (1 / (1 - q) + r) / (1 - q)
我對照了一下標程，確實是這個。 后來我自己推導了一下，發現它可以化成多個等比數列相加的形式，求和后，發現當n趨向于無窮大的時候，它的極限就是上面這個公式。 （注意：i*q^i, 當0<q<1，i趨向于無窮大的時候等于0） 這樣程序就可以寫了。動態規劃保存每個圖的狀態。 如果用python寫，只要建立一個tuple到float的映射就可以了。非常方便。 java中也有List<int>到Double的映射。 c里面估計就得用hash了。 py代碼，參照標程寫的。
fi = open('in')
fo = open('out')
dp = {():0}
ti = 0
def get(s):
if s in dp:
return dp[s]
q = sum([i*(i-1) for i in s])*1.0/2/nn
res = 0
for i in range(len(s)):
for j in range(len(s)):
if i < j:
l = list(s)
del l[max(i,j)]
del l[min(i,j)]
l.append(s[i]+s[j])
l.sort()
r = get(tuple(l))
p = s[i]*s[j]*1.0/nn
res += p*(1+r-r*q)/pow(1-q,2)
dp[s] = res
return res
while 1:
a = fi.readline().split()
if a == None or len(a) != 2:
break
N, M = int(a[0]), int(a[1])
nn = N*(N-1)/2
s = [ i for i in range(N) ]
for i in range(M):
u, v = [ int(i) for i in fi.readline().split() ]
u -= 1
v -= 1
k = s[u]
for j in range(N):
if s[j] == k:
s[j] = s[v]
ss = [ s.count(i) for i in set(s) ]
ss.sort()
print '----', ti
mine = get(tuple(ss))
ans = float(fo.readline().strip())
print 'mine', mine, 'ans', ans
print len(dp)
ti += 1
標程 用很簡潔的代碼寫了并查集，值得借鑒！
import java.util.*;
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
public class interconnect_pm {
private static int nn;
public static void main(String[] args) throws FileNotFoundException {
Scanner in = new Scanner(new File("in"));
PrintWriter out = new PrintWriter("ans.out");
int n = in.nextInt();
nn = (n * (n - 1)) / 2;
int m = in.nextInt();
int[] p = new int[n];
for (int i = 0; i < n; i++) p[i] = i;
for (int i = 0; i < m; i++) {
int u = in.nextInt();
int v = in.nextInt();
u--;
v--;
int k = p[u];
for (int j = 0; j < n; j++) {
if (p[j] == k) {
p[j] = p[v];
}
}
}
List<Integer> st = new ArrayList<Integer>();
for (int i = 0; i < n; i++) {
int s = 0;
for (int j = 0; j < n; j++) {
if (p[j] == i) s++;
}
if (s > 0) {
st.add(s);
}
}
Collections.sort(st);
List<Integer> fn = new ArrayList<Integer>();
fn.add(n);
mem.put(fn, 0.0);
out.println(get(st));
System.out.println(mem.size());
out.close();
}
static Map<List<Integer>, Double> mem = new HashMap<List<Integer>, Double>();
private static double get(List<Integer> st) {
Double ret = mem.get(st);
if (ret != null) return ret;
int m = st.size();
int[][] a = new int[m][m];
for (int i = 0; i < m; i++) {
for (int j = i + 1; j < m; j++) {
a[i][j] = st.get(i) * st.get(j);
}
}
int s = 0;
for (int i = 0; i < m; i++) {
s += st.get(i) * (st.get(i) - 1) / 2;
}
double res = 0;
for (int i = 0; i < m; i++) {
for (int j = i + 1; j < m; j++) {
List<Integer> ss = new ArrayList<Integer>(st.size() - 1);
boolean q = true;
int z = st.get(i) + st.get(j);
for (int k = 0; k < m; k++) {
if (k != i && k != j) {
int zz = st.get(k);
if (q && zz >= z) {
q = false;
ss.add(z);
}
ss.add(zz);
}
}
if (q)
ss.add(z);
double p = a[i][j] * 1.0 / (nn - s);
double e = a[i][j] * 1.0 / ((1 - s * 1.0 / nn) * (1 - s * 1.0 / nn) * nn);
e = e + get(ss) * p;
res += e;
}
}
System.out.println(st);
mem.put(st, res);
return res;
}
}
這題真不是蓋的，要是不看解題報告，恐怕一輩子都做不出來啦。。 題目直接就是要解決一個叫做“最大密度子圖的問題”。 就是在一簡單圖里面找出n個點，這n個點之間有m條邊，讓m/n最大。 這種問題還是有點實際意義的。 算法很復雜，找了一份高中生巨牛寫的文檔（90后真不是蓋的）。http://wenku.baidu.com/view/986baf00b52acfc789ebc9a9.html
。 該文檔描述了一系列的最小割算法，其中包括這個“最大密度子圖問題”。 我編碼能力差，不想寫c代碼，寫了一個py的腳本，能過官方數據，就是速度巨慢，開了一分鐘也沒跑完。。
import sys
def dinic(N, S, T, caps):
to = []
cap = []
head = [[] for i in range(N)]
d = [-1]*N
ans = 0
cut = set()
for a, b, c in caps:
head[a].append(len(cap))
cap.append(c)
to.append(b)
head[b].append(len(cap))
cap.append(0)
to.append(a)
def build():
for i in range(N):
d[i] = -1
q = [S]
d[S] = 0
cut.clear()
while len(q):
x = q[0]
del q[0]
for i in head[x]:
y = to[i]
if cap[i] and d[y] == -1:
d[y] = d[x] + 1
if y == T:
return 1
q.append(y)
cut.add(y)
return 0
def find(x, low):
if x == T:
return low
for i in head[x]:
y = to[i]
if cap[i] and d[y] == d[x] + 1:
f = find(y, min(low, cap[i]))
if f:
cap[i] -= f
cap[i^1] += f
return f
return 0
while build():
while 1:
f = find(S, sum(cap))
if f == 0:
break
ans += f
return ans, cut
def max_weight_closure(V, edges):
inf = sum([abs(i) for i in V])
caps = [(a,b,inf) for a,b in edges]
S = len(V)
T = S + 1
for i in range(len(V)):
if V[i] > 0:
caps.append((S,i,V[i]))
elif V[i] < 0:
caps.append((i,T,-V[i]))
flow, cut = dinic(len(V)+2, S, T, caps)
return sum([V[i] for i in cut]), cut
def max_density_subgraph(N, edges):
def solve(g):
V = [-g]*N
E = []
for u,v in edges:
ve = len(V)
E += [(ve,u), (ve,v)]
V.append(1)
w, cut = max_weight_closure(V, E)
if len(cut) == 0:
w = -1
return w, cut
l = 1.0/N
r = len(edges)
while l < r - 0.01:
m = (l + r) / 2
if solve(m)[0] < 0:
r = m
else:
l = m
w, cut = solve(l)
l = [ i for i in cut if i < N]
if len(l) == 0:
l = [0]
return l
def get_density(N, edges, sel):
e = float(len([1 for a,b in edges if a in sel and b in sel]))
return e/float(len(sel))
fi = open('3155.in')
fo = open('3155.out')
g = lambda x : [ int(i) for i in x.readline().split(' ') ]
ti = 0
while 1:
l = g(fi)
if len(l) == 0:
break
N, M = l
print '----', ti
print 'N M', N, M
E = [ [j-1 for j in g(fi)] for i in range(M)]
cut = max_density_subgraph(N, E)
k = g(fo)[0]
ans = [g(fo)[0]-1 for i in range(k)]
d_ans = get_density(N, E, ans)
d_mine = get_density(N, E, cut)
print 'mine', d_mine
print 'ans', d_ans
if abs(d_ans - d_mine) > 0.001:
print 'error'
break
ti += 1
可以認為，新的平分點和舊的平分點中一定有一個點是重合的。 這樣此題就變成了一個純模擬的問題了。 寫了個腳本，可以過官方的數據。
import sys
f = sys.stdin
D = 10000.0
for s in f.readlines():
n, m = [ int(i) for i in s.split(' ') ]
m += n
b = 0
ans = 0
g = lambda x,y: D*x/y
for a in range(n):
while g(b, m) <= g(a, n):
b += 1
d = min(abs(g(b, m) - g(a, n)), abs(g(b - 1, m) - g(a, n)))
ans += d
print ans
這題對我來說太難啦，看了報告半天才弄明白是咋回事。 高手們的解題報告相當飄逸。我來寫一個造福菜鳥的。 首先來看一下Sample里的第一組數據。 1 2 2 1 2 經過一次變換之后就成了 5 5 5 5 4 它的原理就是 a0 a1 a2 a3 a4 -> (a4+a0+a1) (a0+a1+a2) (a1+a2+a3) (a2+a3+a4) (a3+a4+a0) 如果用矩陣相乘來描述，那就可以表述為1xN和NxN的矩陣相乘，結果仍為1xN矩陣 a = 1 2 2 1 2 b = 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 1 a * b = 5 5 5 5 4 所以最終結果就是：a * (b^k) 線性代數不合格的同鞋表示壓力很大。。 對一個NxN矩陣求k次方，而且這個k很大，N也不小，怎么辦？ 所以有高手觀察到了，這個矩陣長得有點特殊，可以找到一些規律： b^1 = [1, 1, 0, 0, 1] [1, 1, 1, 0, 0] [0, 1, 1, 1, 0] [0, 0, 1, 1, 1] [1, 0, 0, 1, 1] b^2 = [3, 2, 1, 1, 2] [2, 3, 2, 1, 1] [1, 2, 3, 2, 1] [1, 1, 2, 3, 2] [2, 1, 1, 2, 3] b^3 = [7, 6, 4, 4, 6] [6, 7, 6, 4, 4] [4, 6, 7, 6, 4] [4, 4, 6, 7, 6] [6, 4, 4, 6, 7] b^4 = [19, 17, 14, 14, 17] [17, 19, 17, 14, 14] [14, 17, 19, 17, 14] [14, 14, 17, 19, 17] [17, 14, 14, 17, 19] 發現神馬沒有。就是無論是b的幾次冪，都符合A[i][j] = A[i-1][j-1]
高手說是這樣推倒出來地： ““”
利用矩陣A，B具有a[i][j]=A[i-1][j-1],B[i][j]=B[i-1][j-1]（i-1<0則表示i-1+n,j-1<0則表示j-1+n）
我們可以得出矩陣C=a*b也具有這個性質
C[i][j]=sum(A[i][t]*B[t][j])=sum(A[i-1][t-1],B[t-1][j-1])=sum(A[i-1][t],B[t][j-1])=C[i-1][j-1]
“”“ 這樣就可以開一個N大小的數組來存放每次計算的結果了。而沒必要用NxN。 N的問題解決了，但是k還是很大，怎么辦？ 這時候可以用二分法來求b^k b^k = b^1 * b^4 * b^16 。。。 計算過程中，必定會出現數字大于M的情況。 切記 x*y = (x%M)*(y%M) 最后，經過多次優化，這題的代碼居然被高手寫成了如下的一小坨，實在是。。給力哇
#include<iostream>
using namespace std;
int n,m,d,k;
void mul(long long a[],long long b[])
{
int i,j;
long long c[501];
for(i=0;i<n;++i)for(c[i]=j=0;j<n;++j)c[i]+=a[j]*b[i>=j?(i-j):(n+i-j)];
for(i=0;i<n;b[i]=c[i++]%m);
}
long long init[501],tmp[501];
int main()
{
int i,j;
scanf("%d%d%d%d",&n,&m,&d,&k);
for(i=0;i<n;++i)scanf("%I64d",&init[i]);
for(tmp[0]=i=1;i<=d;++i)tmp[i]=tmp[n-i]=1;
while(k)
{
if(k&1)mul(tmp,init);
mul(tmp,tmp);
k>>=1;
}
for(i=0;i<n;++i)if(i)printf(" %I64d",init[i]);else printf("%I64d",init[i]);
printf("\n");
return 0;
}
1. list對象的*操作符
>>> a = [[1]]*10
>>> a
[[1], [1], [1], [1], [1], [1], [1], [1], [1], [1]]
>>> a[1][0] = 2
>>> a
[[2], [2], [2], [2], [2], [2], [2], [2], [2], [2]]
>>>
也就是說，這10個對象實際上是指向的同一個list對象。 這是bug，還是feature？或者是優化？ 總之是蠻讓人火大的就是了。 用 a = [[0] for x in range(10)] 這種寫法就沒有這個問題了。 2. 深拷貝
>>> a = [[0] for x in range(10)]
>>> a
[[0], [0], [0], [0], [0], [0], [0], [0], [0], [0]]
>>> b = list(a)
>>> b
[[0], [0], [0], [0], [0], [0], [0], [0], [0], [0]]
>>> a[1][0] = 2
>>> b
[[0], [2], [0], [0], [0], [0], [0], [0], [0], [0]]
>>>
b = list(a) 意味著a和b中都存放這10個指針。指向[0], [0], [0] .... 這10個對象。 a[1][0] = 2 后 a 自己的值沒有改變，改變的是第二個 [0] 對象。 由于 b 也是指向它的，所以打印b的時候會發現這一點。 這個問題是自己經常犯的問題，大多都是debug半天才知道怎么回事。 使用 import copy b = copy.deepcopy(a) 可以解決這個問題。 3. 如何避免這些問題 要時刻記得，python中的對象就只有兩種，mutable和immutable。也就是可改變和不可改變。 immutable的包括：str tuple int ... mutable可改變的包括：list dict ... immutable的就是原子的。mutable里面存放的都是指向mutable或者immutable的指針。 調試的時候，可以使用id(obj)獲得每個對象的id。這個貌似就是python管理的運行時的對象的地址。 如果發現兩個obj的id相同，那他們就是同一個貨。。
此題看了官方標程，才知道怎么做，其解法實在是相當巧妙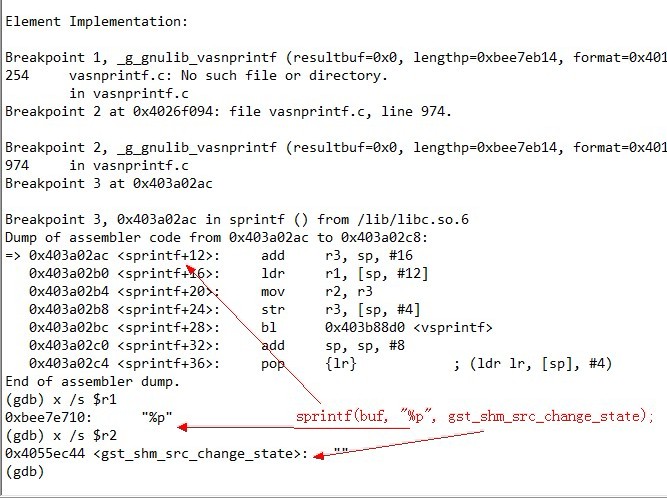！  數據給出的點是順時針順序的，這點非常重要，我們可以根據這個整理出每條線段的方向。 我們可以發現這個規律： 對于某一列格子，在遇到第一條線段之前，一定是空白的，在第一條線段與第二條線段之間，一定是填充的。。以此類推。 而且經過這一列格子的線段數一定是偶數。 標程給出的算法是： 開一個二維數組保存每個格子黑色部分的面積。 如果這個線段是從左到右的，那么就給這條線段以上的格子加上一個負的面積。 如果是從右到左的，則加上一個正的面積。 如果是垂直的，則忽略這條線段。 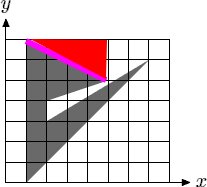  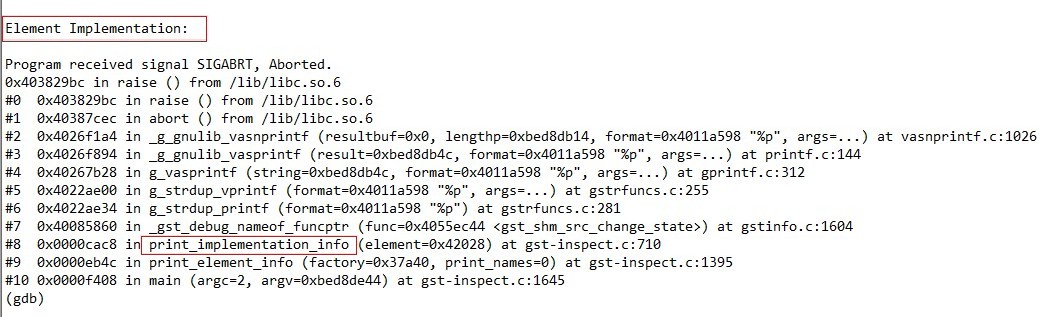 比如說第一條線段是從左到右的，在它以上一共有5個格子，面積依次為：-0.3 -0.6 -1.0 -1.0 -0.6 （大概的數字） 第二條線段是從右到左的，在它以上一共有9個格子，面積依次為：1.0 1.0 1.0 1.0 1.0 1.0 0.6 0.5 0.3 第三條線段是垂直的，忽略它。 第四條線段是從左到右的，在它以上一共有16個格子。。（其中有一個很小很小的） 等等。 給這些格子加上或正或負的增量之后，會發現，恰好完全空白的地方的面積都是0，都被抵消了。 而部分黑色的格子，它的值也是正確的。這就是這個算法的神奇之處～ 標程在這里
{$APPTYPE CONSOLE}
{$R+,Q+,S+,H+,O-}
uses
Math, SysUtils;
Type
Integer=LongInt;
Real=Extended;
Const
TaskID='ascii';
InFile=TaskID+'.in';
OutFile=TaskID+'.out';
MaxN=100;
MaxSize=100;
Eps=1e-12;
Var
N,W,H:Integer;
X,Y:Array[1..MaxN]Of Integer;
Res:Array[-1..MaxSize,-1..MaxSize]Of Real;
Procedure Load;
Var
I:Integer;
Begin
ReSet(Input,InFile);
Read(N,W,H);
For I:=1 To N Do Read(X[I],Y[I]);
Close(Input);
End;
Function Floor(A:Real):Integer;
Begin
Result:=Trunc(A+1000)-1000;
End;
Function Ceil(A:Real):Integer;
Begin
Result:=-Floor(-A);
End;
Procedure Process(X1,Y1,X2,Y2,By:Integer);
Var
I,X,Y,U,D:Integer;
XU,XD,YL,YR,Tmp:Real;
Begin
For X:=X1 To X2-1 Do Begin
YL:=(X-X1)/(X2-X1)*(Y2-Y1)+Y1;
YR:=((X+1)-X1)/(X2-X1)*(Y2-Y1)+Y1;
If YL<YR Then Begin
For I:=0 To Floor(YL)-1 Do Res[X,I]:=Res[X,I]+By;
D:=Floor(YL);
U:=Ceil(YR)-1;
If D=U Then Begin
Res[X,D]:=Res[X,D]+By*(YL-D+YR-D)/2;
End Else If D<U Then Begin
XU:=(D+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,D]:=Res[X,D]+By*(1-(XU-X)*(D+1-YL)/2);
XD:=(U-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,U]:=Res[X,U]+By*((YR-U)*(X+1-XD)/2);
For I:=D+1 To U-1 Do Begin
XU:=(I+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
XD:=(I-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,I]:=Res[X,I]+By*(X+1-XD+X+1-XU)/2;
End;
End;
End Else Begin
For I:=0 To Floor(YR)-1 Do Res[X,I]:=Res[X,I]+By;
D:=Floor(YR);
U:=Ceil(YL)-1;
If D=U Then Begin
Res[X,D]:=Res[X,D]+By*(YL-D+YR-D)/2;
End Else If D<U Then Begin
XU:=(D+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,D]:=Res[X,D]+By*(1-(X+1-XU)*(D+1-YR)/2);
XD:=(U-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,U]:=Res[X,U]+By*((YL-U)*(XD-X)/2);
For I:=D+1 To U-1 Do Begin
XU:=(I+1-Y1)/(Y2-Y1)*(X2-X1)+X1;
XD:=(I-Y1)/(Y2-Y1)*(X2-X1)+X1;
Res[X,I]:=Res[X,I]+By*(XD-X+XU-X)/2;
End;
End;
End;
End;
End;
Procedure Solve;
Var
I,X1,Y1,X2,Y2:Integer;
Begin
FillChar(Res,SizeOf(Res),0);
For I:=1 To N Do Begin
X1:=X[I];
Y1:=Y[I];
X2:=X[I Mod N+1];
Y2:=Y[I Mod N+1];
If X1=X2 Then Continue;
If X1<X2 Then
Process(X1,Y1,X2,Y2,1)
Else
Process(X2,Y2,X1,Y1,-1);
End;
End;
Procedure Save;
Var
X,Y:Integer;
R:Real;
Begin
ReWrite(Output,OutFile);
For Y:=H-1 DownTo 0 Do Begin
For X:=0 To W-1 Do Begin
R:=Res[X,Y];
If R<1/4-Eps Then Write('.') Else If R<1/2-Eps Then Write('+') Else If R<3/4-Eps Then Write('o') Else If R<1-Eps Then Write('$') Else Write('#');
End;
WriteLn;
End;
Close(Output);
End;
begin
Load;
Solve;
Save;
end.
|