polya定理是組合數(shù)學(xué)中比較難的一部分。首先需要對(duì)置換群、集合論有一定的了解，這樣有助于理解burnside引理的證明。其次，polya定理只是對(duì)于在環(huán)上存在旋轉(zhuǎn)、反射等等價(jià)的變換的一種計(jì)數(shù)方法，實(shí)際的題目中很多需要其他的知識(shí)來(lái)進(jìn)行輔助。
　　環(huán)上的計(jì)數(shù)主要就是處理置換 -> 著色這種情況。很關(guān)鍵的一點(diǎn)是同一循環(huán)內(nèi)著色相同。因此很多題目就在置換和著色上下文章。
　　最最簡(jiǎn)單的polya定理題目是置換數(shù)目很少，每種顏色不限，這種情況下只需手工數(shù)出所有的置換就可以了，一般就是一個(gè)公式。
　　難一點(diǎn)的要么是顏色數(shù)有限，需要用排列組合的知識(shí)或動(dòng)態(tài)規(guī)劃來(lái)幫助計(jì)數(shù)；要么是置換非常多，需要利用數(shù)論的知識(shí)來(lái)優(yōu)化。當(dāng)然還有其他的題型，比如對(duì)于相鄰著色的限制，這樣的題目就很困難了。

polya題目：
HOJ 2084 The Colored Cubes
HOJ 2647 Megaminx
POJ 1286 Necklace of Beads
POJ 2409 Let it Bead
TOJ 2795 The Queen's New Necklaces
HDU 1812 Count the Tetris
UVa 11255 Necklace
POJ 2154 Color
POJ 2888 Magic Bracelet
UVa 10601 Cubes
NUAA 1110 n階常系數(shù)線性齊次遞推關(guān)系的解法有很多，特征方程法、生成函數(shù)法，但是對(duì)于編程最實(shí)用的是矩陣解法。
我們定義所要求的f(n) = Ak-1 * f(n - 1) + Ak-2 * f(n - 2) + ... + A0 * f(n-k)，其中f(0)...f(k-1)的初值已經(jīng)給好。
構(gòu)造k * k的矩陣M：

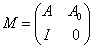
其中A =(Ak-1 Ak-2 ... A1)，I是單位矩陣。
然后構(gòu)造一個(gè)k * 1列向量b：

這樣，M * b之后b0的值就是f(k)，以此類推，M ^ n * b之后b0的值就是f(k-1+n)，算法復(fù)雜度O(k ^ 3 * logn)。

主要分成以下幾個(gè)部分：
　　排列組合與容斥原理
　　二項(xiàng)式定理
　　遞推關(guān)系與生成函數(shù)
　　polya定理

1.排列組合與容斥原理
排列組合里面的4個(gè)重要的基本原理：加法原理、乘法原理、減法原理、除法原理
前面兩個(gè)最為基本，后面兩個(gè)是根據(jù)前兩個(gè)派生出來(lái)的。乘法原理有的時(shí)候的應(yīng)用很巧妙，可以作為一種打開(kāi)思路的辦法。
基本的排列組合之后，接下來(lái)引出了多重集。多重集的排列組合是一個(gè)很經(jīng)典的問(wèn)題，總結(jié)如下：
多重集的排列：
　　全排列的話只需應(yīng)用除法原理就可以了。n個(gè)元素的多重集的r排列需要利用指數(shù)生成函數(shù)來(lái)做。
多重集的組合：
　　n個(gè)元素的多重集的r組合，如果r小于等于任何一個(gè)元素可選的個(gè)數(shù)，那么就歸結(jié)為經(jīng)典的不定方程的解數(shù)問(wèn)題，可以利用“隔板法”來(lái)做。結(jié)果就是一個(gè)組合數(shù)。如果r大于某些元素的可選個(gè)數(shù)，那么一種方法是利用容斥原理，一種方法還是要依靠生成函數(shù)（編程序的時(shí)候可以用動(dòng)歸做）。
如果是一個(gè)環(huán)形的排列組合，那么問(wèn)題就困難許多，要利用置換群和polya定理。
　　單純的依靠四項(xiàng)基本原理來(lái)計(jì)數(shù)，有的時(shí)候會(huì)顯得力不從心，這個(gè)時(shí)候就需要容斥原理的幫助。容斥原理特別適合解決若干限制條件的交、并問(wèn)題，也是打開(kāi)思路的一種方法。
　　利用容斥原理解決的經(jīng)典問(wèn)題有：錯(cuò)排問(wèn)題，帶禁止位置的排列。禁位排列總覺(jué)得用容斥原理解決的不夠優(yōu)美，不知道有沒(méi)有可以編程的數(shù)學(xué)方法。還有一個(gè)困惑的問(wèn)題就是容斥原理和mobius反演的關(guān)系，那個(gè)地方好晦澀。。
　　跟排列組合相關(guān)的還有就是生成排列和組合。生成排列利用那個(gè)什么字典序法好像足夠了，編程好實(shí)現(xiàn)。生成組合方法類似。

2.二項(xiàng)式定理
有很多公式，用的時(shí)候可以現(xiàn)查。終于知道了三角形數(shù)原來(lái)跟排列組合有關(guān)，而且是一個(gè)很簡(jiǎn)潔的公式。
很多公式的推導(dǎo)用的思想很妙。有一個(gè)很好的思想就是把(1 + x) ^ n利用二項(xiàng)式定理展開(kāi)，然后求導(dǎo)、求積分，居然可以導(dǎo)出很多不可思議的公式。
還有一個(gè)很重要的定理就是pascal定理，pascal遞推式很有用（展開(kāi)后有兩種形式，一種是上下限均不定，一種是下限不定），可以解決很多組合數(shù)的求和問(wèn)題。
另外一個(gè)重要的定理就是牛頓二項(xiàng)式定理，在生成函數(shù)中應(yīng)用廣泛，可就是推導(dǎo)起來(lái)有點(diǎn)繁。

3.遞推關(guān)系和生成函數(shù)
　　求解線性遞推關(guān)系的特征方程的方法還是有一定價(jià)值的，但是編程不適用。n解線性齊次遞推方程有矩陣解法。稍微復(fù)雜點(diǎn)的遞推關(guān)系（非線性），特征方程就不夠用了，必須祭出生成函數(shù)這個(gè)有力的武器。感覺(jué)生成函數(shù)實(shí)在是太優(yōu)美、太強(qiáng)大了。生成函數(shù)的關(guān)鍵就是要把多項(xiàng)式拆分成(1-rx)^n這種形式，這樣就可以利用牛頓二項(xiàng)式定理展開(kāi)了。
　　在特殊計(jì)數(shù)序列里面提到了盒裝球問(wèn)題。將p個(gè)不同的球放入k個(gè)相同的盒子（每個(gè)盒子非空）的方法數(shù)是第二類Stirling數(shù)S(p, k)；將p個(gè)相同的球放入k個(gè)相同的盒子（每個(gè)盒子非空）的方法數(shù)是分拆數(shù)，可以歸結(jié)為整數(shù)劃分問(wèn)題，用動(dòng)態(tài)規(guī)劃求解；將p個(gè)不同的盒子放入不同的k個(gè)盒子并且每個(gè)非空的方法數(shù)為k! * S(p, k)。
　　有幾個(gè)很經(jīng)典的遞推關(guān)系：斐波那契數(shù)列、Catalan數(shù)（幾種經(jīng)典的形式：三角剖分?jǐn)?shù)、二叉生成樹(shù)個(gè)數(shù)、+1-1序列、加括號(hào)序列等等）、Stirling數(shù)（兩種，第二種比較常用）、漢諾塔、n個(gè)圓切割平面數(shù)、n條直線k個(gè)交點(diǎn)切割平面數(shù)等等。此外，格路徑中提到的平移、反射和一一對(duì)應(yīng)這三種分析問(wèn)題的方法也很值得借鑒。

4.polya定理

比較復(fù)雜，過(guò)一陣子好好總結(jié)下。 偏序集的兩個(gè)定理：
定理1 令（X,≤）是一個(gè)有限偏序集，并令r是其最大鏈的大小。則X可以被劃分成r個(gè)但不能再少的反鏈。
其對(duì)偶定理稱為Dilworth定理：
定理2 令（X,≤）是一個(gè)有限偏序集，并令m是反鏈的最大的大小。則X可以被劃分成m個(gè)但不能再少的鏈。
說(shuō)白了就是 鏈的最少劃分?jǐn)?shù)=反鏈的最長(zhǎng)長(zhǎng)度
相關(guān)的題目有pku 1065，pku 3636，pku 1548。
這三個(gè)題目可以歸結(jié)為：
　　給定n個(gè)二元組(x, y)，問(wèn)存在最少多少個(gè)劃分使得每個(gè)劃分里面的二元組都滿足x1 <= x2并且y1 <= y2。
　　如果定義x1 <= x2 && y1 <= y2為偏序關(guān)系的話，那么問(wèn)題就轉(zhuǎn)化成求這個(gè)集合的鏈的最少劃分?jǐn)?shù)。可以通過(guò)找最長(zhǎng)反鏈長(zhǎng)度來(lái)解決，這里的反鏈關(guān)系是x1 > x2 || y1 > y2。如果把n個(gè)二元組按照x遞增排序，相同的x按照y遞增排序，那么我們只需對(duì)y找到一個(gè)最長(zhǎng)遞減子序列就是所求的答案，復(fù)雜度O(nlogn)。對(duì)于相同的x之所以按照y遞增排序是因?yàn)檫@里偏序關(guān)系帶等號(hào)，這樣相同的x其實(shí)可以劃分到一起，把y按照遞增排序就可以使得相同的x最多只選擇一個(gè)y。
　　還有的題目要求滿足x1 < x2 && y1 < y2，這就需要把偏序關(guān)系相應(yīng)修改。修改之后對(duì)于相同的x，每一個(gè)都會(huì)被劃分到不同的集合（因?yàn)橄嗟仁遣粷M足偏序關(guān)系的），所以這里的排序關(guān)系要改一下，x相同的y要按照降序排列，這樣求一個(gè)最長(zhǎng)不遞增子序列就是答案，y遞減保證可能會(huì)有多個(gè)x相同的二元組選入到結(jié)果中。
　　可惜對(duì)于貪心做法的正確性依然想不出來(lái)>.< 　　做得很郁悶的一道題。我開(kāi)始已經(jīng)想到是要用置換來(lái)算，但是提交后總是WA。查代碼查了N久也沒(méi)有發(fā)現(xiàn)錯(cuò)誤，感覺(jué)算法又沒(méi)有問(wèn)題。后來(lái)找到往年的解題報(bào)告，才發(fā)現(xiàn)我的基本思路沒(méi)錯(cuò)，但是少考慮了一種情況。我之前認(rèn)為最小代價(jià)等于一個(gè)置換內(nèi)所有元素和 +（元素個(gè)數(shù)-2）* 置換內(nèi)最小元素。但是解題報(bào)告說(shuō)還有一種可能是這個(gè)置換內(nèi)的最小元素和整個(gè)數(shù)列的最小元素交換，然后利用那個(gè)最小元素進(jìn)行交換。這的確會(huì)產(chǎn)生更優(yōu)的解，我原來(lái)怎么想不到呢！
題目代碼：