**機器中float的二進制舍入問題**
在計算機中，對于精度取舍的問題一直都比較模糊，到底什么時候要舍去，什么時候要輸出，下面我就以計算機中的float型為例子，來簡單地說一說float的四舍五“入”。
float型在計算機用32位來表示（4個字節），和計算機表示int長度相同，但是表示的機制完全不一樣，它由sign，exp，frac部分組成，也就是我們所說的符號位，階碼位，和小數位。
具體的表示方法在這里就不細說了（主要談論舍入問題）。我們知道的四舍五入就是小于5舍去，大于等于5就進位，那么為什么要這樣。舉個例子：
1 2 3 4
9 8 7 6 5
比如11，如果在個位運用了四舍五入，那么就會產生一個1的誤差（丟失1）得到10.還有19，如果個位數是9的話，相應的產生了1的誤差（增加1），四舍五入得到20.所以9個數字中1234恰好和9876對應（后面會說到5），我們期望的是在大量的數據下產生的誤差中得到和失去的概率近似為1/2，這就有了四舍五入。但是，我們知道5并沒有什么數字和它對應，所以增加的期望值要大于減小的期望值，這是我們不希望看到的。
但是在計算機中所用的表示方法都是二進制的，1,0出現的概率我們可以認為相等。所以，我們就得到了一個新型的四舍五入的方法，小于所對應精度1/2就舍去，大于就進位，等于就有兩種情況，一種情況是最低有效位是1，進位。為0，舍去。（向偶取整）
用一道例題來說明：
#include<stdio.h> main() { float a; double b; a = 123456.789e4; b = 123456.789e4; printf(“%f/n%f/n”,a,b); }
運行結果如下：
1234567936.000000
1234567890.000000
由于double的尾數位沒有進行舍入操作，因此并沒有改變原數，但1234567890>2^23-1要進行舍入操作。
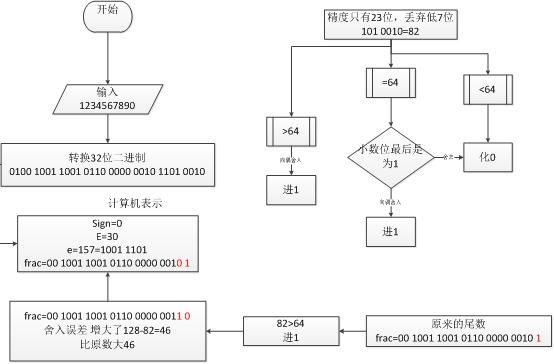
所以就增加了46。