最近兩天在看圓周率的算法,網上流傳這么一個經典的算法,
?1
#include
<
stdio.h
>
?2
long
?a
=
10000
,b
=
0
,c
=
2800
,d,e,f[
2801
],g;?
?3
void
?main()?
?4
{??
?5
????printf(
"
%d
"
,b);
?6
????
for
(;b
!=
c;)?
?7
????
{?
?8
????????f[b]
=
a
/
5
;?
?9
????????b
++
;?
10
????}
?
11
????
for
(;?d
=
0
,g
=
c
*
2
;?c
-=
14
,printf(
"
%.4d
"
,e
+
d
/
a),e
=
d
%
a)?
12
????
for
(b
=
c;d
+=
f[b]
*
a,f[b]
=
d
%--
g,d
/=
g
--
,
--
b;d
*=
b);??
13
}
?
14
??????? 實際上,我看f[2080]和e都是沒有初始化的,f[2080]應初始化為a/5,e初始化為0.
上機驗證了一下,算出來打印256位,對比圓周率表(附后),可知答案是正確的,但是打印256位之后,程序卡在那兒不動,不知道是哪陷入了死循環.
?????? 至于到底有什么問題,還望大蝦幫忙看一看.
?????? 先不管它,這個程序雖然風格惡劣(“短小精悍”讓人看不懂),但這個算法還是值得研究的.畢竟,它是確定性算法,比各種隨機版本(比如蒙特卡羅法模擬)的算法要可靠.
一、源程序
本文分析下面這個很流行的計算PI的小程序。下面這個程序初看起來似乎摸不到頭腦，
不過不用擔心，當你讀完本文的時候就能夠基本讀懂它了。
程序一：很牛的計算Pi的程序
int
?a
=
10000
,b,c
=
2800
,d,e,f[
2801
],g;
main()?
{
for
(;b
-
c;)
????f[b
++
]
=
a
/
5
;
for
(;d
=
0
,g
=
c
*
2
;c?
-=
14
,printf(
"
%.4d
"
,e
+
d
/
a),e
=
d
%
a)
????
for
(b
=
c;?d
+=
f[b]
*
a,f[b]
=
d
%--
g,d
/=
g
--
,
--
b;?d
*=
b);
}
二、數學公式
數學家們研究了數不清的方法來計算PI,這個程序所用的公式如下：
?? 
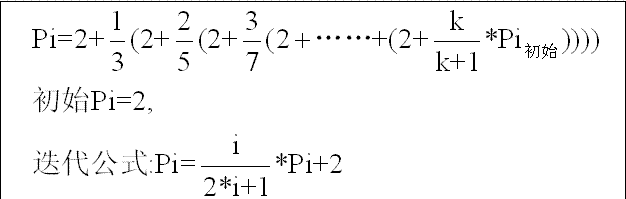
至于這個公式為什么能夠計算出PI，已經超出了本文的能力范圍。
下面要做的事情就是要分析清楚程序是如何實現這個公式的。
我們先來驗證一下這個公式：
程序二：Pi公式驗證程序
#include "stdio.h"
void main()
{
?? float pi=2;
?? int? i;
?? for(i=100;i>=1;i--)
????? pi=pi*(float)i/(2*i+1)+2;
?? printf("%f\n",pi);
?? getchar();
}
上面這個程序的結果是3.141593。
三、程序展開
在正式分析程序之前，我們需要對程序一進行一下展開。我們可以看出程序一都是使用for循環來完成計算的，這樣做雖然可以使得程序短小，但是卻很難讀懂。根據for循環的運行順序，我們可以把它展開為如下while循環的程序：
程序三：for轉換為while之后的程序
?1
int
?a
=
10000
,b,c
=
2800
,d,e,f[
2801
],g;
?2
main()?
{
?3
int
?i;
?4
for
(i
=
0
;i
<
c;i
++
)
?5
?????f[i]
=
a
/
5
;
?6
while
(c
!=
0
)
?7
?????
{
?8
?????????d
=
0
;
?9
?????????g
=
c
*
2
;
10
?????????b
=
c;
11
?????????
while
(
1
)
12
????????????
{
13
????????????????d
=
d
+
f[b]
*
a;
14
????????????????g
--
;
15
????????????????f[b]
=
d
%
g;
16
????????????????d
=
d
/
g;
17
????????????????g
--
;
18
????????????????b
--
;
19
????????????????
if
(b
==
0
)?
break
;
20
????????????????d
=
d
*
b;
21
????????????}
22
?????????c
=
c
-
14
;
23
?????????printf(
"
%.4d
"
,e
+
d
/
a);
24
?????????e
=
d
%
a;
25
????}
26
}
27
下面我們就針對展開后的程序來分析。
四、程序分析
要想計算出無限精度的PI，我們需要上述的迭代公式運行無數次，并且其中每個分數也是完全精確的，這在計算機中自然是無法實現的。那么基本實現思想就是迭代足夠多次，并且每個分數也足夠精確，這樣就能夠計算出PI的前n位來。上面這個程序計算800位，迭代公式一共迭代2800次。
int a=10000,b,c=2800,d,e,f[2801],g;
這句話中的2800就是迭代次數。由于float或者double的精度遠遠不夠，因此程序中使用整數類型（實際是長整型），分段運算（每次計算4位）。我們可以看到輸出語句 printf("%.4d",e+d/a); 其中%.4就是把計算出來的4位輸出，我們看到c每次減少14（ c=c-14;），而c的初始大小為2800，因此一共就分了200段運算，并且每次輸出4位，所以一共輸出了800位。
要是想每次計算3位或5位,怎么辦?首先得unsigned long才可以一次計算5位.
c的大小隨便改,舉個例子: 比如,
a=100000,c=c-14,迭代2800次,共循環200次,輸出1000位
a=1000,c=c-7,迭代2800次,共循環400次,輸出1200位
由于使用整型數運算，因此有必要乘上一個系數，在這個程序中系數為1000，也就是說，公式如下：
?
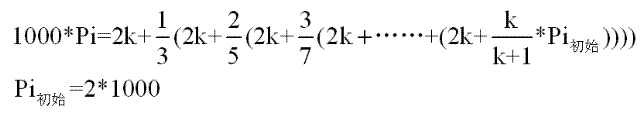
這里的2k表示2000，也就是f[2801]數組初始化以后的數據,a=10000,a/5=2000,所以下面的程序把f中的每個元素都賦值為2000：
?1
for
(i
=
0
;i
<
c;i
++
)
?2
?????f[i]
=
a
/
5
;你可能會覺得奇怪，為什么這里要把一個常數儲存到數組中去，請繼續往下看。
?3
我們先來跟蹤一下程序的運行：
?4
while
(c
!=
0
)??假設這是第一次運行，c
=
2800
，為迭代次數
?5
?????
{
?6
?????????d
=
0
;
?7
?????????g
=
c
*
2
;??這里的g是用來做k
/
(2k
+
1
)中的分母
?8
?????????b
=
c;????這里的b是用來做k
/
(2k
+
1
)中的分子
?9
?????????
while
(
1
)
10
?????????
while
(
1
)
11
????????????
{
12
????????????????d
=
d
+
f[b]
*
a;?f中的所有的值都為2000，這里在計算時又把系數擴大了a
=
10000倍。這樣做的目的稍候介紹，你可以看到輸出的時候是d
/
a,所以這不影響計算.
13
????????????????g
--
;
14
????????????????f[b]
=
d
%
g;?先不管這一行
15
????????????????d
=
d
/
g;???第一次運行的g為2
*
2799
+
1
，你可以看到g做了分母
16
????????????????g
--
;
17
????????????????b
--
;
18
????????????????
if
(b
==
0
)?
break
;
19
????????????????d
=
d
*
b;?這里的b為2799，可以看到d做了分子。
20
????????????}
21
?????????c
=
c
-
14
;
22
?????????printf(
"
%.4d
"
,e
+
d
/
a);
23
?????????e
=
d
%
a;
24
????}
25
只需要粗略的看看上面的程序，我們就大概知道它的確是使用的那個迭代公式來計算Pi
的了，不過不知道到現在為止你是否明白了f數組的用處。如果沒有明白，請繼續閱讀。
?d=d/g,這一行的目的是除以2k+1，我們知道之所以程序無法精確計算的原因就是這個除法。即使用浮點數，答案也是不夠精確的，因此直接用來計算800位的Pi是不可能的。那么不精確的成分在哪里？很明顯：就是那個余數d%g。程序用f數組把這個誤差儲存起來，再下次計算的時候使用。現在你也應該知道為什么d=d+f[b]*a;中間需要乘上a了吧。
把分子擴大之后，才好把誤差精確的算出來。
d如果不乘10000這個系數，則其值為2000，那么運行d=d/g；則是2000/(2*2799+1)，這種整數的除法答案為0，根本無法迭代下去了。
現在我們知道程序就是把余數儲存起來，作為下次迭代的時候的參數，那么為什么這么做就可以使得下次迭代出來的結果為接下來的4位數呢？
這實際上和我們在紙上作除法很類似：
?
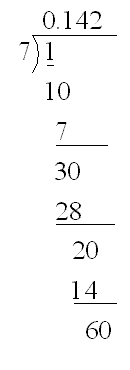
我們可以發現，在做除法的時候，我們通常把余數擴大之后再來計算，f中既然儲存的是余數，而f[b]*a;則正好把這個余數擴大了a倍，然后如此循環下去，可以計算到任意精度。
這里要說明的是，事實上每次計算出來的d并不一定只有4位數，例如第一次計算的時候，d的值為31415926，輸出4位時候，把低四位的值儲存在e中間，e=d%a，也就是5926。最后，這個c=c-14不太好理解。事實上沒有這條語句，程序計算出來的仍然正確。只是因為如果迭代2800次，無論分數如何精確，最后Pi的精度只能夠達到800。
你可以把程序改為如下形式嘗試一下：
for
(i
=
0
;i
<
800
;i
++
)
?????
{
?????
{
?????????d
=
0
;
?????????g
=
c
*
2
;
?????????b
=
c;
?????????
while
(
1
)
????????????
{
????????????????d
=
d
+
f[b]
*
a;
????????????????g
--
;
????????????????f[b]
=
d
%
g;
????????????????d
=
d
/
g;
????????????????g
--
;
????????????????b
--
;
????????????????
if
(b
==
0
)?
break
;
????????????????d
=
d
*
b;
????????????}
????????
//
?c=c-14;?不要這句話。
?????????printf(
"
%.4d
"
,e
+
d
/
a);
?????????e
=
d
%
a;
????}
最后的答案仍然正確。
不過我們可以看到內循環的次數是c次，也就是說每次迭代計算c次。而每次計算后續位
數的時候，迭代次數減少14，而不影響精度。
附:圓周率小數點后1000位：
1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
想要1000萬位的發email給我就是.
posted on 2006-11-09 15:18
哈哈 閱讀(2655)
評論(4) 編輯 收藏 引用