[轉載]隨機數產生原理及應用
原創作者:EmilMatthew
摘要 :
本文簡述了隨機數的產生原理，并用 C 語言實現了迭代取中法，乘同余法等隨機數產生方法，同時，還給出了在符合某種概率分布的隨機變量的產生方法。
關鍵詞 : 偽隨機數產生，概率分布 , 正態隨機數 , 泊松隨機數 , 高斯隨機數
1 前言 :
在用計算機編制程序時，經常需要用到隨機數，尤其在仿真等領域，更對隨機數的產生提出了較高的要求，僅僅使用 C 語言類庫中的隨機函數已難以勝任相應的工作。
用投色子計數的方法產生真正的隨機數 , 但電腦若也這樣做 , 將會占用大量內存 ; 用噪聲發生器或放射性物質也可產生真正的隨機數 , 但不可重復 .
而用數學方法產生最適合計算機 , 這就是周期有限 , 易重復的 ” 偽隨機數 ”
注 : 這里生成的隨機數所處的分布為 0-1 區間上的均勻分布。不是 0-1 區間怎么辦 ? 除以 (high-low), 再加上 low 不就行了 . 我們需要的隨機數序列應具有非退化性，周期長，相關系數小等優點。
2.1 迭代取中法： ( 鄙視它 )
這里在迭代取中法中介紹平方取中法 , 其迭代式如下 :
Xn+1=(Xn^2/10^s)(mod 10^2s)
Rn+1=Xn+1/10^2s
其中， Xn+1 是迭代算子，而 Rn+1 則是每次需要產生的隨機數 。
第一個式子表示的是將 Xn 平方后右移 s 位，并截右端的 2s 位。
而第二個式子則是將截尾后的數字再壓縮 2s 倍，顯然 :0=<Rn+1<=1.
迭代取中法有一個不良的性就是它比較容易退化成 0.
實現 : 網上一大把 , 略 .
2.2 乘同余法：
乘同余法的迭代式如下 :
Xn+1=Lamda*Xn(mod M) (Lamda 即參數λ )
Rn+1=Xn/M
各參數意義及各步的作用可參 2.1
當然，這里的參數的選取至關重要 .
經過前人檢驗的兩組性能較好的素數取模乘同余法迭代式的系數為 :
1 ） lamda=5^5,M=2^35-31
2 ） lamda=7^5,M=2^31-1
實現 : 請注意，這里一定要用到 double long, 否則計算 2^32 會溢出
2.3 混合同余法： C++ 中的 rand() 就是這么實現的 , 偽隨機 , 故使用前一定要加 srand() 來隨機取種 , 這樣每次實驗結果才不會相同 .
混合同余法是加同余法和乘同余法的混合形式 , 其迭代式如下 :
Xn+1=( Lamda*Xn+C )%M
Rn+1=Xn/M
經前人研究表明，在 M=2^q 的條件下，參數 lamda,miu,X0 按如下選取，周期較大，概率統計特性好 :
Lamda=2^b+1,b 取 q/2 附近的數
C=(1/2+sqrt(3))/M
X0 為任意非負整數
它的一個致命的弱點，那就是隨機數的生成在某一周期內成線性增長的趨勢，顯然，在大多數場合，這種極富“規律”型的隨機數是不應當使用的。
實現 :
1 
double _random( void )
2 
{
3 
int a;
4 double r;
5
6 a = rand() % 32767 ;
7 r = (a + 0.00 ) / 32767.00 ;
8
9 return r;
10
11 
}
3連續型隨機變量的生成:
3.1 反函數法 : 又叫反變換法 , 記住 , 它首先需要使用均勻分布獲得一個 (0,1) 間隨機數 , 這個隨機數相當于原概率分布的 Y 值 , 因為我們現在是反過來求 X. 哎 , 聽糊涂了也沒關系 , 只要知道算法怎么執行的就行 .
采用概率積分變換原理 , 對于隨機變量 X 的分布函數 F(X) 可以求其反函數，得 : 原來我們一般面對的是概率公式 Y=f(X). 現在反過來 , 由已知的概率分布或通過其參數信息來反求 X.
Xi=G(Ri)
其中 ,Ri 為一個 0-1 區間內的均勻分布的隨機變量 .
F(X) 較簡單時，求解較易，當 F(X) 較復雜時，需要用到較為復雜的變換技巧。
可能你沒明白 , 看 3.1.1 的例子就一定會明白 .
3.1.1 平均分布 :
已知隨機變量密度函數為 :
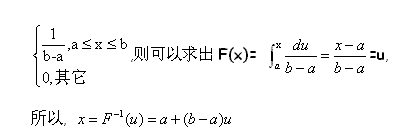
3.1.2 指數分布 :
指數分布的分布函數為 :
x<0 時 ,F(x)=0 ; x>=0,F(x)=1-exp(-lamda*x)
利用反函數法，可以求得 : x=-lnR/lamda( 怎么來的別問 )
3.2 正態分布隨機變量的生成 :
正態分布在概率統計的理論及應用中占有重要地位，因此，能產生符合正態分布的隨機變量就在模擬一類的工作中占有相當重要的地位。
下面介紹兩種方法。
3.2.1
經過一定的計算變行，符合二維的正態分布的隨機變量的生成可按下面的方法進行：
1) 產生位于 0-1 區間上的兩個隨機數 r1 和 r2.
2) 計算 u=2*r1-1,v=2*r2-1 及 w=u^2+v^2
3) 若 w>1 ，則返回 1)
4) x=u[(-lnw)/w]^(1/2) ( 怎么來的別問 )
y=v[(-lnw)/w]^(1/2)
如果為 (miu,sigma^2) 正態分布 , 則按上述方法產生 x 后， x’=miu+sigma*x
由于采用基于乘同余法生成的 0-1 上的隨機數的正態分布隨機數始終無法能過正態分布總體均值的假設檢驗。而采用 C 語言的庫函數中的隨機數生成函數 rand() 來產生 0-1 上的隨機數，效果較為理想。
3.2.2 利用中心極限定理生成符合正態分布的隨機量：
根據獨立同分布的中心極限定理，有 :
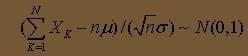
這里，其實只要取 n=12 （這里，亦即生成 12 個 0-1 上的隨機數序列）就會有比較好的效果。
經驗證，用該種方法生成生的隨機數序列同樣能比較好的符合正態分布特性。
由于生成的都是標準正態分布，所以，當需要生成 N(a,b) 的正態分布隨機量時，根據正態分布的線性變換特性，只要用 x=a*x0+b 即可。（其中， x0 表示生成的符合 N(0,1) 分布的正態隨機變量。方法 3.1 亦是如此）
實現 :
1 : double _sta( double mu, double sigma) // 利用中心極限定理生成
2 {
3 int i;
4 double r,sum = 0.0 ;
5
6 if (sigma <= 0.0 ) { printf( " Sigma<=0.0 in _sta! " ); exit( 1 ); }
7 for (i = 1 ;i <= 12 ;i ++ )
8 sum = sum + _random();
9 r = (sum - 6.00 ) * sigma + mu;
10
11 return r;
12
13 }
14
1 double _sta2( double mu, double sigma) // 利用反函數法公式x=u[(-lnw)/w]^(1/2)
2 {
3 double r1,r2;
4
5 r1 = _random();
6 r2 = _random();
7
8 return sqrt( - 2 * log(r1)) * cos( 2 * M_PI * r2) * sigma + mu ;
9
10 }
4 離散型隨機變量的生成 :
離散型隨機變量的生成主要是希望得到在已知 X 符合某類分布的條件下，生成相應的 X 。
4.1 符合泊松分布的隨機變量的生成 :
這里，采用 ” 上限攔截 ” 法進行測試 ，我看了不懂 , 希望有人幫我分析一下 , 從數學角度幫我分析一下,謝謝!
基本的思想是這樣的：
1 ）在泊松分布中，求出 X 取何值時， p(X=k) 取最大值時，設為 Pxmax.
其時，這樣當于求解 f(x)=lamda^k/k! 在 k 取何值時有最大值，雖然，這道題有一定的難度，但在程序中可以能過一個循環來得到取得 f(x) 取最大值時的整數自變量 Xmax 。
2) 通過迭代，不斷生成 0-1 區間上的隨機數，當隨機數 <Pxmax 時，則終止迭代，否則重復 (2)
3) 記錄迭代過程的次數，即為所需要得到的符何泊松分布的隨機量。
顯然，這種方法較為粗糙，在試驗的過程中發現：生成的的隨機量只能算是近似的服從泊松分布，所以，更為有效的算法還有待嘗試。
實現 : 采用 double 至少可以支持 lamda=700 ，即 exp(-700)!=0
1 const int MAX_VAL = 10000 ;
2 double U_Rand( double a, double b ) // 均勻分布
3 {
4 double x = random( MAX_VAL );
5 return a + (b - a) * x / (MAX_VAL - 1 );
6 }
7 double P_Rand( double Lamda ) // 泊松分布
8 {
9 double x = 0 ,b = 1 ,c = exp( - Lamda ),u;
10 do {
11 u = U_Rand( 0 , 1 );
12 b *= u;
13 if ( b >= c )
14 x ++ ;
15 } while ( b >= c );
16 return x;
17 }
為防止lamda過大而溢出,故應該自己來寫一個浮點類,我不懂,摘抄的.
下面是一個簡單的浮點類，還有一個用該浮點類支持的 Exp ，以及簡單的測試
可以不用位域，而只用整數來表示 double ，然后用移位來進行轉換
這里用位域只是為了簡單和明了（看清 double 的結構）
1 #include < math.h >
2 #include < iostream.h >
3
4 const int nDoubleExponentBias = 0x3ff ;
5
6 typedef struct
7 {
8 unsigned int uSignificand2 : 32 ;
9 unsigned int uSignificand1 : 20 ;
10 unsigned int uExponent : 11 ;
11 unsigned int uSign : 1 ;
12 } DOUBLE_BIT;
13
14 typedef union
15 {
16 double lfDouble;
17 DOUBLE_BIT tDoubleBit;
18 } DOUBLE;
19
20
21 class TFloat
22 {
23 int m_uSign;
24 int m_uExponent;
25 unsigned int m_uSignificand1;
26 unsigned int m_uSignificand2;
27
28
29 public :
30
31 TFloat( void );
32 TFloat( const double lfX );
33 TFloat( const TFloat & cX );
34
35 TFloat & operator *= ( const TFloat & cX );
36 bool operator <= ( const TFloat & cX );
37
38 void GetFromDouble( double lfX );
39 double ToDouble( void ); // for test
40 } ;
4.2符合二項分布的隨機變量的生成:
符合二項分布的隨機變量產生類似上限攔截法，不過效果要好許多，這是由二項分布的特點決定的。
具體方法如下:
設二項分布B(p,n)，其中，p為每個單獨事件發生的概率：
關鍵算法:
i=0;reTimes=0
while(i<n)
{
temp=myrand();//生成0-1區間上的隨機變量
if(temp>1-p)
reTimes++;
i++;
}
顯然，直觀的看來，這種算法將每個獨立的事件當作一個0-1分布來做，生成的0-1區間上的隨機數，若小于1-p則不發生，否則認為發生，這樣的生成方式較為合理。實驗結果也驗證了其合理性。
4.3高斯分布隨機數:貼一個最經典的程序,看程序大概就知道高斯分布函數的反函數了.
#include <stdlib.h>
#include <math.h>
double gaussrand()
{
static double V1, V2, S;
static int phase = 0;
double X;
if ( phase == 0 ) {
do {
double U1 = (double)rand() / RAND_MAX;
double U2 = (double)rand() / RAND_MAX;
V1 = 2 * U1 - 1;
V2 = 2 * U2 - 1;
S = V1 * V1 + V2 * V2;
} while(S >= 1 || S == 0);
X = V1 * sqrt(-2 * log(S) / S);
} else
X = V2 * sqrt(-2 * log(S) / S);
phase = 1 - phase;
return X;
}
posted on 2006-11-08 18:52
哈哈 閱讀(14855)
評論(16) 編輯 收藏 引用