第一篇：從決策樹學(xué)習(xí)談到貝葉斯分類算法、EM、HMM
引言
最近在面試中，除了基礎(chǔ) & 算法 & 項(xiàng)目之外，經(jīng)常被問到或被要求介紹和描述下自己所知道的幾種分類或聚類算法，而我向來恨對(duì)一個(gè)東西只知其皮毛而不得深入，故寫一個(gè)有關(guān)聚類 & 分類算法的系列文章以作為自己備試之用(盡管貌似已無多大必要，但還是覺得應(yīng)該寫下以備將來常常回顧思考)。行文雜亂，但僥幸若能對(duì)讀者也起到一定幫助，則幸甚至哉。
本分類 & 聚類算法系列借鑒和參考了兩本書，一本是Tom M.Mitchhell所著的機(jī)器學(xué)習(xí)，一本是數(shù)據(jù)挖掘?qū)д摚@兩本書皆分別是機(jī)器學(xué)習(xí) & 數(shù)據(jù)挖掘領(lǐng)域的開山 or 杠鼎之作，讀者有繼續(xù)深入下去的興趣的話，不妨在閱讀本文之后，課后細(xì)細(xì)研讀這兩本書。除此之外，還參考了網(wǎng)上不少牛人的作品(文末已注明參考文獻(xiàn)或鏈接)，在此，皆一一表示感謝。
本分類 & 聚類算法系列暫稱之為Top 10 Algorithms in Data Mining，其中，各篇分別有以下具體內(nèi)容：
- 開篇：決策樹學(xué)習(xí)Decision Tree，與貝葉斯分類算法(含隱馬可夫模型HMM)；
- 第二篇：支持向量機(jī)SVM(support vector machine)，與神經(jīng)網(wǎng)絡(luò)ANN；
- 第三篇：待定...
說白了，一年多以前，我在本blog內(nèi)寫過一篇文章，叫做：數(shù)據(jù)挖掘領(lǐng)域十大經(jīng)典算法初探(題外話：最初有個(gè)出版社的朋友便是因此文找到的我，盡管現(xiàn)在看來，我離出書日期仍是遙遙無期)。現(xiàn)在，我抽取其中幾個(gè)最值得一寫的幾個(gè)算法每一個(gè)都寫一遍，以期對(duì)其有個(gè)大致通透的了解。
OK，全系列任何一篇文章若有任何錯(cuò)誤，漏洞，或不妥之處，還請(qǐng)讀者們一定要隨時(shí)不吝賜教 & 指正，謝謝各位。
概念點(diǎn)一、理念論與模板匹配，經(jīng)驗(yàn)論與機(jī)器學(xué)習(xí)
哲學(xué)界現(xiàn)有兩種理論，
- 一種是柏拉圖建立 的“理念論”（或譯“相論”），認(rèn)為理念型相（共相）是獨(dú)立于紛繁復(fù)雜的可感事物存在的，是永恒而完美的。而諸多的可感事物只不過是這個(gè)永恒而完美的理念的復(fù)制品、“影子”，從中世紀(jì)基督教哲學(xué)的視角來看，這種立場即是“共相先于可感事物而存在”，并且“共相決定可感事物”，是一種自上而下的、獨(dú)斷論的思維方式。
- 而亞里士多德反對(duì)這種做法，認(rèn)為一般（共相）就在個(gè)別之中。
由此形成了從經(jīng)驗(yàn)個(gè)別事物抽象出共相的、自下而上的經(jīng)驗(yàn)主義者與獨(dú)斷論者兩種思維方式的對(duì)立。經(jīng)驗(yàn)論和獨(dú)斷論，孰是孰非，不知道哲學(xué)發(fā)展到今天，尚無定論，但是從模式識(shí)別半個(gè)多世紀(jì)的發(fā)展來看，似乎經(jīng)驗(yàn)論占了上風(fēng)。
在模式識(shí)別中，最初主要使用的模板匹配的方法，下面以人臉檢測為例。人臉檢測，就是要在一幅給定的圖片中，判斷是否存在人臉，如若存在，人臉的位置和大小幾何。所謂模板匹配，就是事先人為規(guī)定一個(gè)模板，包含人臉的形狀，眼睛鼻子等的位置，然后以此模板去匹配給定圖片。這個(gè)過程，可以認(rèn)為是柏拉圖“理念論”的一種具體方法，柏拉圖所說的“理念”就是此處的模板。
而隨著模式識(shí)別的發(fā)展，模板匹配方法的局限性越來越嚴(yán)重，主流方法也逐漸轉(zhuǎn)變到基于統(tǒng)計(jì)學(xué)的機(jī)器學(xué)習(xí)(Machine Learning)方法上來。所謂機(jī)器學(xué)習(xí)的方法，同樣以人臉檢測為例，可以理解為把計(jì)算機(jī)當(dāng)成一個(gè)無知的小孩，然后給他很多人臉的圖片，告訴他這是人臉，通過計(jì)算機(jī)的自我訓(xùn)練與學(xué)習(xí)，以此形成一個(gè)人臉的”模式“，然后依次”模式“去對(duì)給定的圖片做人臉檢測。這個(gè)過程，可以認(rèn)為是亞里士多德經(jīng)驗(yàn)主義學(xué)說，即從個(gè)別事物中學(xué)習(xí)、抽象出共通的性質(zhì)。
本文所介紹的絕大數(shù)多數(shù)方法或算法便是由上述經(jīng)驗(yàn)論所引申而來的理論。
概念點(diǎn)二、分類與聚類
在講具體的分類和聚類算法之前，有必要講一下什么是分類，什么是聚類，都包含哪些具體算法或問題。
常見的分類與聚類算法
簡單來說，自然語言處理中，我們經(jīng)常提到的文本分類便就是一個(gè)分類問題，一般的模式分類方法都可用于文本分類研究。常用的分類算法包括：樸素的貝葉斯分類算法(native Bayesian classifier)、基于支持向量機(jī)(SVM)的分類器，k-最近鄰法(k-nearest neighbor，kNN)，神經(jīng)網(wǎng)絡(luò)法，決策樹分類法，模糊分類法等等(本篇稍后會(huì)講決策樹分類與貝葉斯分類算法，當(dāng)然，所有這些分類算法日后在本blog內(nèi)都會(huì)一一陸續(xù)闡述)。
而K均值聚類則是最典型的聚類算法。
監(jiān)督學(xué)習(xí)與無監(jiān)督學(xué)習(xí)
一般來說，機(jī)器學(xué)習(xí)方法分為監(jiān)督學(xué)習(xí)方法，和無監(jiān)督學(xué)習(xí)方法。舉個(gè)具體的對(duì)應(yīng)例子，則是比如說，在詞義消岐中，也分為監(jiān)督的消岐方法，和無監(jiān)督的消岐方法。在有監(jiān)督的消岐方法中，訓(xùn)練數(shù)據(jù)是已知的，即沒歌詞的語義分類是被標(biāo)注了的；而在無監(jiān)督的消岐方法中，訓(xùn)練數(shù)據(jù)是未經(jīng)標(biāo)注的(愛思考同時(shí)又頭腦活躍的讀者，腦袋中可能立馬蹦出一個(gè)問題，就是：此處的無監(jiān)督學(xué)習(xí)方法跟上文概念點(diǎn)一內(nèi)所述的獨(dú)斷論是否有聯(lián)系?歡迎想清楚了，告訴我)。
有監(jiān)督的學(xué)習(xí)也通常稱為分類任務(wù)，而無監(jiān)督的學(xué)習(xí)通常稱為聚類任務(wù)。也就是說，分類屬于監(jiān)督學(xué)習(xí)，聚類屬于無監(jiān)督學(xué)習(xí)。
再舉個(gè)例子，正如人們通過已知病例學(xué)習(xí)診斷技術(shù)那樣，計(jì)算機(jī)要通過學(xué)習(xí)才能具有識(shí)別各種事物和現(xiàn)象的能力。用來進(jìn)行學(xué)習(xí)的材料就是與被識(shí)別對(duì)象屬于同類的有限數(shù)量樣本。監(jiān)督學(xué)習(xí)中在給予計(jì)算機(jī)學(xué)習(xí)樣本的同時(shí)，還告訴計(jì)算各個(gè)樣本所屬的類別。若所給的學(xué)習(xí)樣本不帶有類別信息,就是無監(jiān)督學(xué)習(xí)(淺顯點(diǎn)說：同樣是學(xué)習(xí)訓(xùn)練，監(jiān)督學(xué)習(xí)中，給的樣例比如是已經(jīng)標(biāo)注了如心臟病的，肝炎的；而無監(jiān)督學(xué)習(xí)中，就是給你一大堆的樣例，沒有標(biāo)明是何種病例的)。
第一部分、決策樹學(xué)習(xí)
1.1、什么是決策樹
咱們直接切入正題。所謂決策樹，顧名思義，是一種樹，一種依托于策略抉擇而建立起來的樹。
機(jī)器學(xué)習(xí)中，決策樹是一個(gè)預(yù)測模型；他代表的是對(duì)象屬性與對(duì)象值之間的一種映射關(guān)系。樹中每個(gè)節(jié)點(diǎn)表示某個(gè)對(duì)象，而每個(gè)分叉路徑則代表的某個(gè)可能的屬性值，而每個(gè)葉結(jié)點(diǎn)則對(duì)應(yīng)從根節(jié)點(diǎn)到該葉節(jié)點(diǎn)所經(jīng)歷的路徑所表示的對(duì)象的值。決策樹僅有單一輸出，若欲有復(fù)數(shù)輸出，可以建立獨(dú)立的決策樹以處理不同輸出。
從數(shù)據(jù)產(chǎn)生決策樹的機(jī)器學(xué)習(xí)技術(shù)叫做決策樹學(xué)習(xí), 通俗點(diǎn)說就是決策樹。
來理論的太過抽象，下面舉兩個(gè)淺顯易懂的例子：
第一個(gè)例子
套用俗語，決策樹分類的思想類似于找對(duì)象。現(xiàn)想象一個(gè)女孩的母親要給這個(gè)女孩介紹男朋友，于是有了下面的對(duì)話：
女兒：多大年紀(jì)了？
母親：26。
女兒：長的帥不帥？
母親：挺帥的。
女兒：收入高不？
母親：不算很高，中等情況。
女兒：是公務(wù)員不？
母親：是，在稅務(wù)局上班呢。
女兒：那好，我去見見。
這個(gè)女孩的決策過程就是典型的分類樹決策。相當(dāng)于通過年齡、長相、收入和是否公務(wù)員對(duì)將男人分為兩個(gè)類別：見和不見。假設(shè)這個(gè)女孩對(duì)男人的要求是：30歲以下、長相中等以上并且是高收入者或中等以上收入的公務(wù)員，那么這個(gè)可以用下圖表示女孩的決策邏輯：
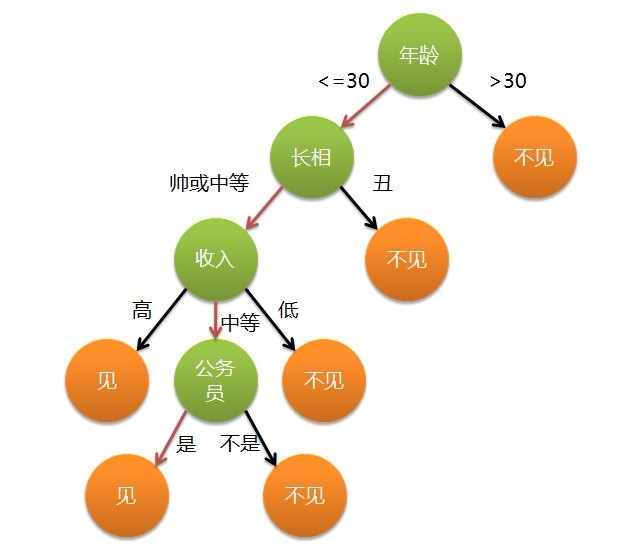
也就是說，決策樹的簡單策略就是，好比公司招聘面試過程中篩選一個(gè)人的簡歷，如果你的條件相當(dāng)好比如說某985/211重點(diǎn)大學(xué)博士畢業(yè)，那么二話不說，直接叫過來面試，如果非重點(diǎn)大學(xué)畢業(yè)，但實(shí)際項(xiàng)目經(jīng)驗(yàn)豐富，那么也要考慮叫過來面試一下，即所謂具體情況具體分析、決策。
第二個(gè)例子
此例子來自Tom M.Mitchell著的機(jī)器學(xué)習(xí)一書：
小王的目的是通過下周天氣預(yù)報(bào)尋找什么時(shí)候人們會(huì)打高爾夫，他了解到人們決定是否打球的原因最主要取決于天氣情況。而天氣狀況有晴，云和雨；氣溫用華氏溫度表示；相對(duì)濕度用百分比；還有有無風(fēng)。如此，我們便可以構(gòu)造一棵決策樹，如下（根據(jù)天氣這個(gè)分類決策這天是否合適打網(wǎng)球）：
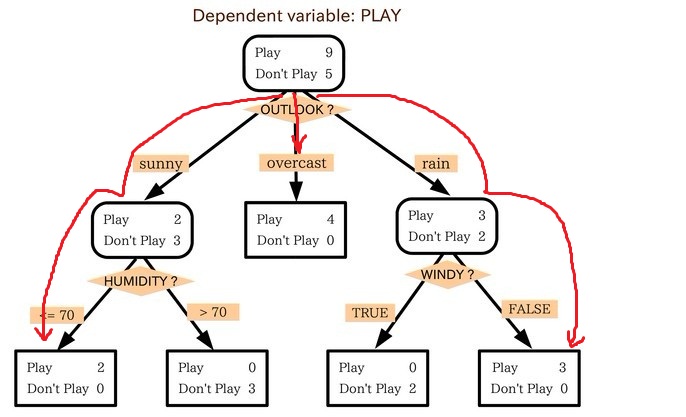
上述決策樹對(duì)應(yīng)于以下表達(dá)式：
（Outlook=Sunny ^Humidity<=70）V （Outlook = Overcast）V （Outlook=Rain ^ Wind=Weak）
1.2、ID3算法
1.2.1、決策樹學(xué)習(xí)之ID3算法
ID3算法是決策樹算法的一種。想了解什么是ID3算法之前，我們得先明白一個(gè)概念：奧卡姆剃刀。
- 奧卡姆剃刀（Occam's Razor, Ockham's Razor），又稱“奧坎的剃刀”，是由14世紀(jì)邏輯學(xué)家、圣方濟(jì)各會(huì)修士奧卡姆的威廉（William of Occam，約1285年至1349年）提出，他在《箴言書注》2卷15題說“切勿浪費(fèi)較多東西，去做‘用較少的東西，同樣可以做好的事情’。簡單點(diǎn)說，便是：be simple。
ID3算法（Iterative Dichotomiser 3 迭代二叉樹3代）是一個(gè)由Ross Quinlan發(fā)明的用于決策樹的算法。這個(gè)算法便是建立在上述所介紹的奧卡姆剃刀的基礎(chǔ)上：越是小型的決策樹越優(yōu)于大的決策樹（be simple簡單理論）。盡管如此，該算法也不是總是生成最小的樹形結(jié)構(gòu)，而是一個(gè)啟發(fā)式算法。
OK，從信息論知識(shí)中我們知道，期望信息越小，信息增益越大，從而純度越高。ID3算法的核心思想就是以信息增益度量屬性選擇，選擇分裂后信息增益(很快，由下文你就會(huì)知道信息增益又是怎么一回事)最大的屬性進(jìn)行分裂。該算法采用自頂向下的貪婪搜索遍歷可能的決策樹空間。
所以，ID3的思想便是：
- 自頂向下的貪婪搜索遍歷可能的決策樹空間構(gòu)造決策樹(此方法是ID3算法和C4.5算法的基礎(chǔ))；
- 從“哪一個(gè)屬性將在樹的根節(jié)點(diǎn)被測試”開始；
- 使用統(tǒng)計(jì)測試來確定每一個(gè)實(shí)例屬性單獨(dú)分類訓(xùn)練樣例的能力，分類能力最好的屬性作為樹的根結(jié)點(diǎn)測試(如何定義或者評(píng)判一個(gè)屬性是分類能力最好的呢？這便是下文將要介紹的信息增益，or 信息增益率)。
- 然后為根結(jié)點(diǎn)屬性的每個(gè)可能值產(chǎn)生一個(gè)分支，并把訓(xùn)練樣例排列到適當(dāng)?shù)姆种Вㄒ簿褪钦f，樣例的該屬性值對(duì)應(yīng)的分支）之下。
- 重復(fù)這個(gè)過程，用每個(gè)分支結(jié)點(diǎn)關(guān)聯(lián)的訓(xùn)練樣例來選取在該點(diǎn)被測試的最佳屬性。
這形成了對(duì)合格決策樹的貪婪搜索，也就是算法從不回溯重新考慮以前的選擇。
下圖所示即是用于學(xué)習(xí)布爾函數(shù)的ID3算法概要：
1.2.2、哪個(gè)屬性是最佳的分類屬性
1、信息增益的度量標(biāo)準(zhǔn)：熵
上文中，我們提到：“ID3算法的核心思想就是以信息增益度量屬性選擇，選擇分裂后信息增益(很快，由下文你就會(huì)知道信息增益又是怎么一回事)最大的屬性進(jìn)行分裂。”接下來，咱們就來看看這個(gè)信息增益是個(gè)什么概念(當(dāng)然，在了解信息增益之前，你必須先理解：信息增益的度量標(biāo)準(zhǔn)：熵)。
上述的ID3算法的核心問題是選取在樹的每個(gè)結(jié)點(diǎn)要測試的屬性。我們希望選擇的是最有利于分類實(shí)例的屬性，信息增益(Information Gain)是用來衡量給定的屬性區(qū)分訓(xùn)練樣例的能力，而ID3算法在增長樹的每一步使用信息增益從候選屬性中選擇屬性。
為了精確地定義信息增益，我們先定義信息論中廣泛使用的一個(gè)度量標(biāo)準(zhǔn)，稱為熵（entropy），它刻畫了任意樣例集的純度（purity）。給定包含關(guān)于某個(gè)目標(biāo)概念的正反樣例的樣例集S，那么S相對(duì)這個(gè)布爾型分類的熵為：
上述公式中，p+代表正樣例，比如在本文開頭第二個(gè)例子中p+則意味著去打羽毛球，而p-則代表反樣例，不去打球(在有關(guān)熵的所有計(jì)算中我們定義0log0為0)。
如果寫代碼實(shí)現(xiàn)熵的計(jì)算，則如下所示：
-
- double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){
- vector<int> count (2,0);
- unsigned int i,j;
- bool done_flag = false;
- for(j = 1; j < MAXLEN; j++){
- if(done_flag) break;
- if(!attribute_row[j].compare(attribute)){
- for(i = 1; i < remain_state.size(); i++){
- if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){
- if(!remain_state[i][MAXLEN - 1].compare(yes)){
- count[0]++;
- }
- else count[1]++;
- }
- }
- done_flag = true;
- }
- }
- if(count[0] == 0 || count[1] == 0 ) return 0;
-
- double sum = count[0] + count[1];
- double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);
- return entropy;
- }
舉例來說，假設(shè)S是一個(gè)關(guān)于布爾概念的有14個(gè)樣例的集合，它包括9個(gè)正例和5個(gè)反例（我們采用記號(hào)[9+，5-]來概括這樣的數(shù)據(jù)樣例），那么S相對(duì)于這個(gè)布爾樣例的熵為：
Entropy（[9+，5-]）=-（9/14）log2（9/14）-（5/14）log2（5/14）=0.940。
So，根據(jù)上述這個(gè)公式，我們可以得到：S的所有成員屬于同一類，Entropy(S)=0； S的正反樣例數(shù)量相等，Entropy(S)=1；S的正反樣例數(shù)量不等，熵介于0，1之間，如下圖所示：
信息論中對(duì)熵的一種解釋，熵確定了要編碼集合S中任意成員的分類所需要的最少二進(jìn)制位數(shù)。更一般地，如果目標(biāo)屬性具有c個(gè)不同的值，那么S相對(duì)于c個(gè)狀態(tài)的分類的熵定義為：
Pi為子集合中不同性(而二元分類即正樣例和負(fù)樣例)的樣例的比例。
2、信息增益度量期望的熵降低
信息增益Gain(S,A)定義
已經(jīng)有了熵作為衡量訓(xùn)練樣例集合純度的標(biāo)準(zhǔn)，現(xiàn)在可以定義屬性分類訓(xùn)練數(shù)據(jù)的效力的度量標(biāo)準(zhǔn)。這個(gè)標(biāo)準(zhǔn)被稱為“信息增益（information gain）”。簡單的說，一個(gè)屬性的信息增益就是由于使用這個(gè)屬性分割樣例而導(dǎo)致的期望熵降低(或者說，樣本按照某屬性劃分時(shí)造成熵減少的期望)。更精確地講，一個(gè)屬性A相對(duì)樣例集合S的信息增益Gain(S,A)被定義為：
其中 Values(A)是屬性A所有可能值的集合，是S中屬性A的值為v的子集。換句話來講，Gain(S,A)是由于給定屬性A的值而得到的關(guān)于目標(biāo)函數(shù)值的信息。當(dāng)對(duì)S的一個(gè)任意成員的目標(biāo)值編碼時(shí)，Gain(S,A)的值是在知道屬性A的值后可以節(jié)省的二進(jìn)制位數(shù)。
接下來，有必要提醒讀者一下：關(guān)于下面這兩個(gè)概念 or 公式，
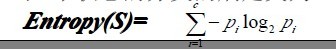
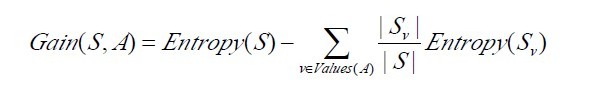
第一個(gè)Entropy(S)是熵定義，第二個(gè)則是信息增益Gain(S,A)的定義，而Gain(S,A)由第一個(gè)Entropy(S)計(jì)算出，記住了。
下面，舉個(gè)例子，假定S是一套有關(guān)天氣的訓(xùn)練樣例，描述它的屬性包括可能是具有Weak和Strong兩個(gè)值的Wind。像前面一樣，假定S包含14個(gè)樣例，[9+，5-]。在這14個(gè)樣例中，假定正例中的6個(gè)和反例中的2個(gè)有Wind =Weak，其他的有Wind=Strong。由于按照屬性Wind分類14個(gè)樣例得到的信息增益可以計(jì)算如下。
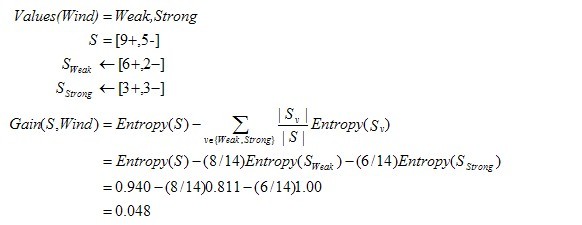
運(yùn)用在本文開頭舉得第二個(gè)根據(jù)天氣情況是否決定打羽毛球的例子上，得到的最佳分類屬性如下圖所示：
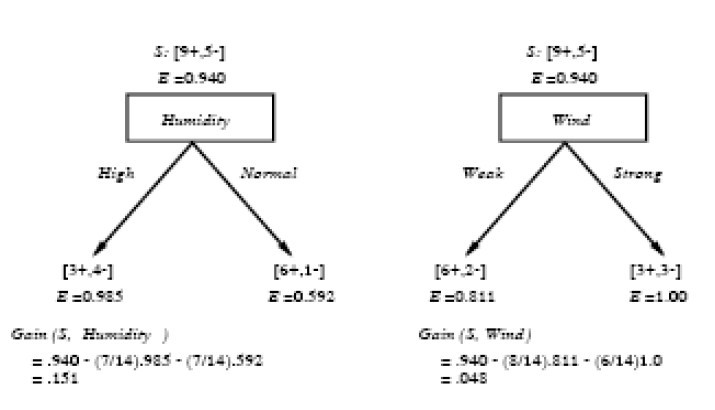
在上圖中，計(jì)算了兩個(gè)不同屬性：濕度(humidity)和風(fēng)力(wind)的信息增益，最終humidity這種分類的信息增益0.151>wind增益的0.048。說白了，就是在星期六上午是否適合打網(wǎng)球的問題訣策中，采取humidity較wind作為分類屬性更佳，決策樹由此而來。
-
-
-
-
-
- Node * BulidDecisionTreeDFS(Node * p, vector <vector <string> > remain_state, vector <string> remain_attribute){
-
-
-
- if (p == NULL)
- p = new Node();
-
- if (AllTheSameLabel(remain_state, yes)){
- p->attribute = yes;
- return p;
- }
- if (AllTheSameLabel(remain_state, no)){
- p->attribute = no;
- return p;
- }
- if(remain_attribute.size() == 0){
- string label = MostCommonLabel(remain_state);
- p->attribute = label;
- return p;
- }
-
- double max_gain = 0, temp_gain;
- vector <string>::iterator max_it;
- vector <string>::iterator it1;
- for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++){
- temp_gain = ComputeGain(remain_state, (*it1));
- if(temp_gain > max_gain) {
- max_gain = temp_gain;
- max_it = it1;
- }
- }
-
- vector <string> new_attribute;
- vector <vector <string> > new_state;
- for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++){
- if((*it2).compare(*max_it)) new_attribute.push_back(*it2);
- }
-
- p->attribute = *max_it;
- vector <string> values = map_attribute_values[*max_it];
- int attribue_num = FindAttriNumByName(*max_it);
- new_state.push_back(attribute_row);
- for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++){
- for(unsigned int i = 1; i < remain_state.size(); i++){
- if(!remain_state[i][attribue_num].compare(*it3)){
- new_state.push_back(remain_state[i]);
- }
- }
- Node * new_node = new Node();
- new_node->arrived_value = *it3;
- if(new_state.size() == 0){
- new_node->attribute = MostCommonLabel(remain_state);
- }
- else
- BulidDecisionTreeDFS(new_node, new_state, new_attribute);
-
- p->childs.push_back(new_node);
- new_state.erase(new_state.begin()+1,new_state.end());
- }
- return p;
- }
1.2.3、ID3算法決策樹的形成
OK，下圖為ID3算法第一步后形成的部分決策樹。這樣綜合起來看，就容易理解多了。1、overcast樣例必為正，所以為葉子結(jié)點(diǎn)，總為yes；2、ID3無回溯，局部最優(yōu)，而非全局最優(yōu)，還有另一種樹后修剪決策樹。下圖是ID3算法第一步后形成的部分決策樹：
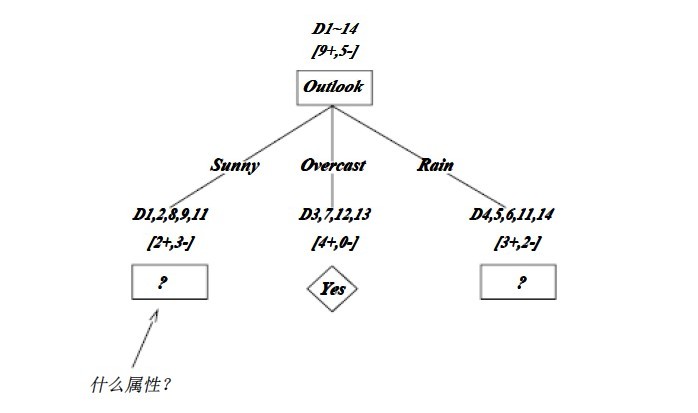
如上圖，訓(xùn)練樣例被排列到對(duì)應(yīng)的分支結(jié)點(diǎn)。分支Overcast的所有樣例都是正例，所以成為目標(biāo)分類為Yes的葉結(jié)點(diǎn)。另兩個(gè)結(jié)點(diǎn)將被進(jìn)一步展開，方法是按照新的樣例子集選取信息增益最高的屬性。
1.3、C4.5算法
1.3.1、ID3算法的改進(jìn)：C4.5算法
C4.5，是機(jī)器學(xué)習(xí)算法中的另一個(gè)分類決策樹算法，它是決策樹(決策樹也就是做決策的節(jié)點(diǎn)間的組織方式像一棵樹，其實(shí)是一個(gè)倒樹)核心算法，也是上文1.2節(jié)所介紹的ID3的改進(jìn)算法，所以基本上了解了一半決策樹構(gòu)造方法就能構(gòu)造它。
決策樹構(gòu)造方法其實(shí)就是每次選擇一個(gè)好的特征以及分裂點(diǎn)作為當(dāng)前節(jié)點(diǎn)的分類條件。
既然說C4.5算法是ID3的改進(jìn)算法，那么C4.5相比于ID3改進(jìn)的地方有哪些呢？：
- 用信息增益率來選擇屬性。ID3選擇屬性用的是子樹的信息增益，這里可以用很多方法來定義信息，ID3使用的是熵(entropy，熵是一種不純度度量準(zhǔn)則),也就是熵的變化值，而C4.5用的是信息增益率。對(duì)，區(qū)別就在于一個(gè)是信息增益，一個(gè)是信息增益率。
- 在樹構(gòu)造過程中進(jìn)行剪枝，在構(gòu)造決策樹的時(shí)候，那些掛著幾個(gè)元素的節(jié)點(diǎn)，不考慮最好，不然容易導(dǎo)致overfitting。
- 對(duì)非離散數(shù)據(jù)也能處理。
- 能夠?qū)Σ煌暾麛?shù)據(jù)進(jìn)行處理
針對(duì)上述第一點(diǎn)，解釋下：一般來說率就是用來取平衡用的，就像方差起的作用差不多，比如有兩個(gè)跑步的人，一個(gè)起點(diǎn)是10m/s的人、其10s后為20m/s；另一個(gè)人起速是1m/s、其1s后為2m/s。如果緊緊算差值那么兩個(gè)差距就很大了，如果使用速度增加率(加速度，即都是為1m/s^2)來衡量，2個(gè)人就是一樣的加速度。因此，C4.5克服了ID3用信息增益選擇屬性時(shí)偏向選擇取值多的屬性的不足。
C4.5算法之信息增益率
OK，既然上文中提到C4.5用的是信息增益率，那增益率的具體是如何定義的呢？：
是的，在這里，C4.5算法不再是通過信息增益來選擇決策屬性。一個(gè)可以選擇的度量標(biāo)準(zhǔn)是增益比率gain ratio（Quinlan 1986）。增益比率度量是用前面的增益度量Gain(S，A)和分裂信息度量SplitInformation(S，A)來共同定義的，如下所示：
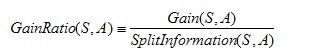
其中，分裂信息度量被定義為(分裂信息用來衡量屬性分裂數(shù)據(jù)的廣度和均勻)：
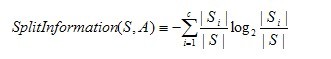
其中S1到Sc是c個(gè)值的屬性A分割S而形成的c個(gè)樣例子集。注意分裂信息實(shí)際上就是S關(guān)于屬性A的各值的熵。這與我們前面對(duì)熵的使用不同，在那里我們只考慮S關(guān)于學(xué)習(xí)到的樹要預(yù)測的目標(biāo)屬性的值的熵。
請(qǐng)注意，分裂信息項(xiàng)阻礙選擇值為均勻分布的屬性。例如，考慮一個(gè)含有n個(gè)樣例的集合被屬性A徹底分割（譯注：分成n組，即一個(gè)樣例一組）。這時(shí)分裂信息的值為log2n。相反，一個(gè)布爾屬性B分割同樣的n個(gè)實(shí)例，如果恰好平分兩半，那么分裂信息是1。如果屬性A和B產(chǎn)生同樣的信息增益，那么根據(jù)增益比率度量，明顯B會(huì)得分更高。
使用增益比率代替增益來選擇屬性產(chǎn)生的一個(gè)實(shí)際問題是，當(dāng)某個(gè)Si接近S（|Si|»|S|）時(shí)分母可能為0或非常小。如果某個(gè)屬性對(duì)于S的所有樣例有幾乎同樣的值，這時(shí)要么導(dǎo)致增益比率未定義，要么是增益比率非常大。為了避免選擇這種屬性，我們可以采用這樣一些啟發(fā)式規(guī)則，比如先計(jì)算每個(gè)屬性的增益，然后僅對(duì)那些增益高過平均值的屬性應(yīng)用增益比率測試（Quinlan 1986）。
除了信息增益，Lopez de Mantaras（1991）介紹了另一種直接針對(duì)上述問題而設(shè)計(jì)的度量，它是基于距離的（distance-based）。這個(gè)度量標(biāo)準(zhǔn)基于所定義的一個(gè)數(shù)據(jù)劃分間的距離尺度。具體更多請(qǐng)參看：Tom M.Mitchhell所著的機(jī)器學(xué)習(xí)之3.7.3節(jié)。
1.3.2、C4.5算法構(gòu)造決策樹的過程
- Function C4.5(R:包含連續(xù)屬性的無類別屬性集合,C:類別屬性,S:訓(xùn)練集)
-
- Begin
- If S為空,返回一個(gè)值為Failure的單個(gè)節(jié)點(diǎn);
- If S是由相同類別屬性值的記錄組成,
- 返回一個(gè)帶有該值的單個(gè)節(jié)點(diǎn);
- If R為空,則返回一個(gè)單節(jié)點(diǎn),其值為在S的記錄中找出的頻率最高的類別屬性值;
- [注意未出現(xiàn)錯(cuò)誤則意味著是不適合分類的記錄]；
- For 所有的屬性R(Ri) Do
- If 屬性Ri為連續(xù)屬性，則
- Begin
- 將Ri的最小值賦給A1：
- 將Rm的最大值賦給Am；
- For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m;
- 將Ri點(diǎn)的基于{< =Aj,>Aj}的最大信息增益屬性(Ri,S)賦給A；
- End；
- 將R中屬性之間具有最大信息增益的屬性(D,S)賦給D;
- 將屬性D的值賦給{dj/j=1,2...m}；
- 將分別由對(duì)應(yīng)于D的值為dj的記錄組成的S的子集賦給{sj/j=1,2...m};
- 返回一棵樹，其根標(biāo)記為D;樹枝標(biāo)記為d1,d2...dm;
- 再分別構(gòu)造以下樹:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
1.3.3、C4.5算法實(shí)現(xiàn)中的幾個(gè)關(guān)鍵步驟
在上文中，我們已經(jīng)知道了決策樹學(xué)習(xí)C4.5算法中4個(gè)重要概念的表達(dá)，如下：
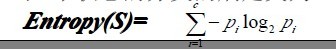
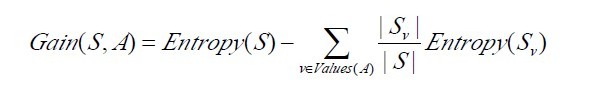
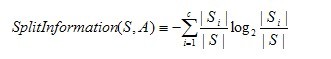
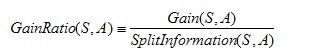
接下來，咱們寫下代碼實(shí)現(xiàn)，
1、信息熵
- double C4_5::entropy(int *attrClassCount, int classNum, int allNum){
- double iEntropy = 0.0;
- for(int i = 0; i < classNum; i++){
- double temp = ((double)attrClassCount[i]) / allNum;
- if(temp != 0.0)
- iEntropy -= temp * (log(temp) / log(2.0));
- }
- return iEntropy;
- }
2、信息增益率
- double C4_5::gainRatio(int classNum, vector<int *> attriCount, double pEntropy){
- int* attriNum = new int[attriCount.size()];
- int allNum = 0;
-
- for(int i = 0; i < (int)attriCount.size(); i++){
- attriNum[i] = 0;
- for(int j = 0; j < classNum; j++){
- attriNum[i] += attriCount[i][j];
- allNum += attriCount[i][j];
- }
- }
- double gain = 0.0;
- double splitInfo = 0.0;
- for(int i = 0; i < (int)attriCount.size(); i++){
- gain -= ((double)attriNum[i]) / allNum * entropy(attriCount[i], classNum, attriNum[i]);
- splitInfo -= ((double)attriNum[i]) / allNum * (log(((double)attriNum[i])/allNum) / log(2.0));
- }
- gain += pEntropy;
- delete[] attriNum;
- return (gain / splitInfo);
- }
3、選取最大增益屬性作為分類條件
- int C4_5::chooseAttribute(vector<int> attrIndex, vector<int *>* sampleCount){
- int bestIndex = 0;
- double maxGainRatio = 0.0;
- int classNum = (int)(decisions[attrIndex[(int)attrIndex.size()-1]]).size();
-
-
- int* temp = new int[classNum];
- int allNum = 0;
- for(int i = 0; i < classNum; i++){
- temp[i] = sampleCount[(int)attrIndex.size()-1][i][i];
- allNum += temp[i];
- }
- double pEntropy = entropy(temp, classNum, allNum);
- delete[] temp;
-
-
- for(int i = 0; i < (int)attrIndex.size()-1; i++){
- double gainR = gainRatio(classNum, sampleCount[i], pEntropy);
- if(gainR > maxGainRatio){
- bestIndex = i;
- maxGainRatio = gainR;
- }
- }
- return bestIndex;
- }
4、還有一系列建樹，打印樹的步驟，此處略過。
1.4、決策樹歸納的特點(diǎn)
- form Wind：決策樹使用于特征取值離散的情況，連續(xù)的特征一般也要處理成離散的(而很多文章沒有表達(dá)出決策樹的關(guān)鍵特征or概念)。實(shí)際應(yīng)用中，決策樹overfitting比較的嚴(yán)重，一般要做boosting。分類器的性能上不去，很主要的原因在于特征的鑒別性不足，而不是分類器的好壞，好的特征才有好的分類效果，分類器只是弱相關(guān)。
- 那如何提高 特征的鑒別性呢？一是設(shè)計(jì)特征時(shí)盡量引入domain knowledge，二是對(duì)提取出來的特征做選擇、變換和再學(xué)習(xí)，這一點(diǎn)是機(jī)器學(xué)習(xí)算法不管的部分。
第二部分、貝葉斯分類
昔人已乘黃鶴去，此地空余黃鶴樓；
黃鶴一去不復(fù)返，白云千載空悠悠。
后便大為折服，已無什興致再提了(偶現(xiàn)在就是這感覺)，然文章還得繼續(xù)寫。So，本文第二部分之大部分基本整理自未鵬兄之手，若有任何不妥之處，還望讀者和未鵬兄海涵，謝謝。
2.1、什么是貝葉斯分類
貝葉斯定理：已知某條件概率，如何得到兩個(gè)事件交換后的概率，也就是在已知P(A|B)的情況下如何求得P(B|A)。這里先解釋什么是條件概率：
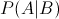表示事件B已經(jīng)發(fā)生的前提下，事件A發(fā)生的概率，叫做事件B發(fā)生下事件A的條件概率。其基本求解公式為：
。
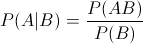貝葉斯定理之所以有用，是因?yàn)槲覀冊(cè)谏钪薪?jīng)常遇到這種情況：我們可以很容易直接得出P(A|B)，P(B|A)則很難直接得出，但我們更關(guān)心P(B|A)，貝葉斯定理就為我們打通從P(A|B)獲得P(B|A)的道路。
下面不加證明地直接給出貝葉斯定理（公式被網(wǎng)友指出有問題，待后續(xù)驗(yàn)證改正）：
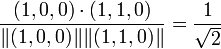
2.2 貝葉斯公式如何而來
貝葉斯公式是怎么來的？下面是wikipedia 上的一個(gè)例子：
一所學(xué)校里面有 60% 的男生，40% 的女生。男生總是穿長褲，女生則一半穿長褲一半穿裙子。有了這些信息之后我們可以容易地計(jì)算“隨機(jī)選取一個(gè)學(xué)生，他（她）穿長褲的概率和穿裙子的概率是多大”，這個(gè)就是前面說的“正向概率”的計(jì)算。然而，假設(shè)你走在校園中，迎面走來一個(gè)穿長褲的學(xué)生（很不幸的是你高度近似，你只看得見他（她）穿的是否長褲，而無法確定他（她）的性別），你能夠推斷出他（她）是男生的概率是多大嗎？
一些認(rèn)知科學(xué)的研究表明（《決策與判斷》以及《Rationality for Mortals》第12章：小孩也可以解決貝葉斯問題），我們對(duì)形式化的貝葉斯問題不擅長，但對(duì)于以頻率形式呈現(xiàn)的等價(jià)問題卻很擅長。在這里，我們不妨把問題重新敘述成：你在校園里面隨機(jī)游走，遇到了 N 個(gè)穿長褲的人（仍然假設(shè)你無法直接觀察到他們的性別），問這 N 個(gè)人里面有多少個(gè)女生多少個(gè)男生。
你說，這還不簡單：算出學(xué)校里面有多少穿長褲的，然后在這些人里面再算出有多少女生，不就行了？
我們來算一算：假設(shè)學(xué)校里面人的總數(shù)是 U 個(gè)。60% 的男生都穿長褲，于是我們得到了 U * P(Boy) * P(Pants|Boy) 個(gè)穿長褲的（男生）（其中 P(Boy) 是男生的概率 = 60%，這里可以簡單的理解為男生的比例；P(Pants|Boy) 是條件概率，即在 Boy 這個(gè)條件下穿長褲的概率是多大，這里是 100% ，因?yàn)樗心猩即╅L褲）。40% 的女生里面又有一半（50%）是穿長褲的，于是我們又得到了 U * P(Girl) * P(Pants|Girl) 個(gè)穿長褲的（女生）。加起來一共是 U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) 個(gè)穿長褲的，其中有 U * P(Girl) * P(Pants|Girl) 個(gè)女生。兩者一比就是你要求的答案。
下面我們把這個(gè)答案形式化一下：我們要求的是 P(Girl|Pants) （穿長褲的人里面有多少女生），我們計(jì)算的結(jié)果是 U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] 。容易發(fā)現(xiàn)這里校園內(nèi)人的總數(shù)是無關(guān)的，可以消去。于是得到
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
注意，如果把上式收縮起來，分母其實(shí)就是 P(Pants) ，分子其實(shí)就是 P(Pants, Girl) 。而這個(gè)比例很自然地就讀作：在穿長褲的人（ P(Pants) ）里面有多少（穿長褲）的女孩（ P(Pants, Girl) ）。
上式中的 Pants 和 Boy/Girl 可以指代一切東西，So，其一般形式就是：
P(A|B) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
收縮起來就是：
P(A|B) = P(AB) / P(B)
其實(shí)這個(gè)就等于：
P(A|B) * P(B) = P(AB)
更進(jìn)一步闡述，P(A|B)便是在條件B的情況下，A出現(xiàn)的概率是多大。然看似這么平凡的貝葉斯公式，背后卻隱含著非常深刻的原理。
2.3、拼寫糾正
經(jīng)典著作《人工智能：現(xiàn)代方法》的作者之一 Peter Norvig 曾經(jīng)寫過一篇介紹如何寫一個(gè)拼寫檢查/糾正器的文章，里面用到的就是貝葉斯方法，這里我們不打算復(fù)述他寫的文章，而是簡要地將其核心思想介紹一下。
首先，我們需要詢問的是：“問題是什么？”
問題是我們看到用戶輸入了一個(gè)不在字典中的單詞，我們需要去猜測：“這個(gè)家伙到底真正想輸入的單詞是什么呢？”用剛才我們形式化的語言來敘述就是，我們需要求：
P(我們猜測他想輸入的單詞 | 他實(shí)際輸入的單詞)
這個(gè)概率。并找出那個(gè)使得這個(gè)概率最大的猜測單詞。顯然，我們的猜測未必是唯一的，就像前面舉的那個(gè)自然語言的歧義性的例子一樣；這里，比如用戶輸入： thew ，那么他到底是想輸入 the ，還是想輸入 thaw ？到底哪個(gè)猜測可能性更大呢？幸運(yùn)的是我們可以用貝葉斯公式來直接出它們各自的概率，我們不妨將我們的多個(gè)猜測記為 h1 h2 .. （ h 代表 hypothesis），它們都屬于一個(gè)有限且離散的猜測空間 H （單詞總共就那么多而已），將用戶實(shí)際輸入的單詞記為 D （ D 代表 Data ，即觀測數(shù)據(jù)），于是
P(我們的猜測1 | 他實(shí)際輸入的單詞)
可以抽象地記為：
P(h1 | D)
類似地，對(duì)于我們的猜測2，則是 P(h2 | D)。不妨統(tǒng)一記為：
P(h | D)
運(yùn)用一次貝葉斯公式，我們得到：
P(h | D) = P(h) * P(D | h) / P(D)
對(duì)于不同的具體猜測 h1 h2 h3 .. ，P(D) 都是一樣的，所以在比較 P(h1 | D) 和 P(h2 | D) 的時(shí)候我們可以忽略這個(gè)常數(shù)。即我們只需要知道：
P(h | D) ∝ P(h) * P(D | h) （注：那個(gè)符號(hào)的意思是“正比例于”，不是無窮大，注意符號(hào)右端是有一個(gè)小缺口的。）
這個(gè)式子的抽象含義是：對(duì)于給定觀測數(shù)據(jù)，一個(gè)猜測是好是壞，取決于“這個(gè)猜測本身獨(dú)立的可能性大小（先驗(yàn)概率，Prior ）”和“這個(gè)猜測生成我們觀測到的數(shù)據(jù)的可能性大小”（似然，Likelihood ）的乘積。具體到我們的那個(gè) thew 例子上，含義就是，用戶實(shí)際是想輸入 the 的可能性大小取決于 the 本身在詞匯表中被使用的可能性（頻繁程度）大小（先驗(yàn)概率）和 想打 the 卻打成 thew 的可能性大小（似然）的乘積。
剩下的事情就很簡單了，對(duì)于我們猜測為可能的每個(gè)單詞計(jì)算一下 P(h) * P(D | h) 這個(gè)值，然后取最大的，得到的就是最靠譜的猜測。更多細(xì)節(jié)請(qǐng)參看未鵬兄之原文。
2.4、貝葉斯的應(yīng)用
2.4.1、中文分詞
貝葉斯是機(jī)器學(xué)習(xí)的核心方法之一。比如中文分詞領(lǐng)域就用到了貝葉斯。浪潮之巔的作者吳軍在《數(shù)學(xué)之美》系列中就有一篇是介紹中文分詞的。這里介紹一下核心的思想，不做贅述，詳細(xì)請(qǐng)參考吳軍的原文。
分詞問題的描述為：給定一個(gè)句子（字串），如：
南京市長江大橋
如何對(duì)這個(gè)句子進(jìn)行分詞（詞串）才是最靠譜的。例如：
1. 南京市/長江大橋
2. 南京/市長/江大橋
這兩個(gè)分詞，到底哪個(gè)更靠譜呢？
我們用貝葉斯公式來形式化地描述這個(gè)問題，令 X 為字串（句子），Y 為詞串（一種特定的分詞假設(shè)）。我們就是需要尋找使得 P(Y|X) 最大的 Y ，使用一次貝葉斯可得：
P(Y|X) ∝ P(Y)*P(X|Y)
用自然語言來說就是 這種分詞方式（詞串）的可能性 乘以 這個(gè)詞串生成我們的句子的可能性。我們進(jìn)一步容易看到：可以近似地將 P(X|Y) 看作是恒等于 1 的，因?yàn)槿我饧傧氲囊环N分詞方式之下生成我們的句子總是精準(zhǔn)地生成的（只需把分詞之間的分界符號(hào)扔掉即可）。于是，我們就變成了去最大化 P(Y) ，也就是尋找一種分詞使得這個(gè)詞串（句子）的概率最大化。而如何計(jì)算一個(gè)詞串：
W1, W2, W3, W4 ..
的可能性呢？我們知道，根據(jù)聯(lián)合概率的公式展開：P(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * .. 于是我們可以通過一系列的條件概率（右式）的乘積來求整個(gè)聯(lián)合概率。然而不幸的是隨著條件數(shù)目的增加（P(Wn|Wn-1,Wn-2,..,W1) 的條件有 n-1 個(gè)），數(shù)據(jù)稀疏問題也會(huì)越來越嚴(yán)重，即便語料庫再大也無法統(tǒng)計(jì)出一個(gè)靠譜的 P(Wn|Wn-1,Wn-2,..,W1) 來。為了緩解這個(gè)問題，計(jì)算機(jī)科學(xué)家們一如既往地使用了“天真”假設(shè)：我們假設(shè)句子中一個(gè)詞的出現(xiàn)概率只依賴于它前面的有限的 k 個(gè)詞（k 一般不超過 3，如果只依賴于前面的一個(gè)詞，就是2元語言模型（2-gram），同理有 3-gram 、 4-gram 等），這個(gè)就是所謂的“有限地平線”假設(shè)。
雖然上面這個(gè)假設(shè)很傻很天真，但結(jié)果卻表明它的結(jié)果往往是很好很強(qiáng)大的，后面要提到的樸素貝葉斯方法使用的假設(shè)跟這個(gè)精神上是完全一致的，我們會(huì)解釋為什么像這樣一個(gè)天真的假設(shè)能夠得到強(qiáng)大的結(jié)果。目前我們只要知道，有了這個(gè)假設(shè)，剛才那個(gè)乘積就可以改寫成： P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. （假設(shè)每個(gè)詞只依賴于它前面的一個(gè)詞）。而統(tǒng)計(jì) P(W2|W1) 就不再受到數(shù)據(jù)稀疏問題的困擾了。對(duì)于我們上面提到的例子“南京市長江大橋”，如果按照自左到右的貪婪方法分詞的話，結(jié)果就成了“南京市長/江大橋”。但如果按照貝葉斯分詞的話（假設(shè)使用 3-gram），由于“南京市長”和“江大橋”在語料庫中一起出現(xiàn)的頻率為 0 ，這個(gè)整句的概率便會(huì)被判定為 0 。 從而使得“南京市/長江大橋”這一分詞方式勝出。
2.4.2、貝葉斯圖像識(shí)別，Analysis by Synthesis
貝葉斯方法是一個(gè)非常 general 的推理框架。其核心理念可以描述成：Analysis by Synthesis （通過合成來分析）。06 年的認(rèn)知科學(xué)新進(jìn)展上有一篇 paper 就是講用貝葉斯推理來解釋視覺識(shí)別的，一圖勝千言，下圖就是摘自這篇 paper ：
首先是視覺系統(tǒng)提取圖形的邊角特征，然后使用這些特征自底向上地激活高層的抽象概念（比如是 E 還是 F 還是等號(hào)），然后使用一個(gè)自頂向下的驗(yàn)證來比較到底哪個(gè)概念最佳地解釋了觀察到的圖像。
2.4.3、最大似然與最小二乘
學(xué)過線性代數(shù)的大概都知道經(jīng)典的最小二乘方法來做線性回歸。問題描述是：給定平面上 N 個(gè)點(diǎn)，（這里不妨假設(shè)我們想用一條直線來擬合這些點(diǎn)——回歸可以看作是擬合的特例，即允許誤差的擬合），找出一條最佳描述了這些點(diǎn)的直線。
一個(gè)接踵而來的問題就是，我們?nèi)绾味x最佳？我們?cè)O(shè)每個(gè)點(diǎn)的坐標(biāo)為 (Xi, Yi) 。如果直線為 y = f(x) 。那么 (Xi, Yi) 跟直線對(duì)這個(gè)點(diǎn)的“預(yù)測”：(Xi, f(Xi)) 就相差了一個(gè) ΔYi = |Yi – f(Xi)| 。最小二乘就是說尋找直線使得 (ΔY1)^2 + (ΔY2)^2 + .. （即誤差的平方和）最小，至于為什么是誤差的平方和而不是誤差的絕對(duì)值和，統(tǒng)計(jì)學(xué)上也沒有什么好的解釋。然而貝葉斯方法卻能對(duì)此提供一個(gè)完美的解釋。
我們假設(shè)直線對(duì)于坐標(biāo) Xi 給出的預(yù)測 f(Xi) 是最靠譜的預(yù)測，所有縱坐標(biāo)偏離 f(Xi) 的那些數(shù)據(jù)點(diǎn)都含有噪音，是噪音使得它們偏離了完美的一條直線，一個(gè)合理的假設(shè)就是偏離路線越遠(yuǎn)的概率越小，具體小多少，可以用一個(gè)正態(tài)分布曲線來模擬，這個(gè)分布曲線以直線對(duì) Xi 給出的預(yù)測 f(Xi) 為中心，實(shí)際縱坐標(biāo)為 Yi 的點(diǎn) (Xi, Yi) 發(fā)生的概率就正比于 EXP[-(ΔYi)^2]。（EXP(..) 代表以常數(shù) e 為底的多少次方）。
現(xiàn)在我們回到問題的貝葉斯方面，我們要想最大化的后驗(yàn)概率是：
P(h|D) ∝ P(h) * P(D|h)
又見貝葉斯！這里 h 就是指一條特定的直線，D 就是指這 N 個(gè)數(shù)據(jù)點(diǎn)。我們需要尋找一條直線 h 使得 P(h) * P(D|h) 最大。很顯然，P(h) 這個(gè)先驗(yàn)概率是均勻的，因?yàn)槟臈l直線也不比另一條更優(yōu)越。所以我們只需要看 P(D|h) 這一項(xiàng)，這一項(xiàng)是指這條直線生成這些數(shù)據(jù)點(diǎn)的概率，剛才說過了，生成數(shù)據(jù)點(diǎn) (Xi, Yi) 的概率為 EXP[-(ΔYi)^2] 乘以一個(gè)常數(shù)。而 P(D|h) = P(d1|h) * P(d2|h) * .. 即假設(shè)各個(gè)數(shù)據(jù)點(diǎn)是獨(dú)立生成的，所以可以把每個(gè)概率乘起來。于是生成 N 個(gè)數(shù)據(jù)點(diǎn)的概率為 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化這個(gè)概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。 熟悉這個(gè)式子嗎？
除了以上所介紹的之外，貝葉斯還在詞義消岐，語言模型的平滑方法中都有一定應(yīng)用。下節(jié)，咱們?cè)賮砗唵慰聪聵闼刎惾~斯方法。
2.5、樸素貝葉斯方法
樸素貝葉斯方法是一個(gè)很特別的方法，所以值得介紹一下。在眾多的分類模型中，應(yīng)用最為廣泛的兩種分類模型是決策樹模型(Decision Tree Model)和樸素貝葉斯模型（Naive Bayesian Model，NBC）。 樸素貝葉斯模型發(fā)源于古典數(shù)學(xué)理論，有著堅(jiān)實(shí)的數(shù)學(xué)基礎(chǔ)，以及穩(wěn)定的分類效率。
同時(shí)，NBC模型所需估計(jì)的參數(shù)很少，對(duì)缺失數(shù)據(jù)不太敏感，算法也比較簡單。理論上，NBC模型與其他分類方法相比具有最小的誤差率。但是實(shí)際上并非總是如此，這是因?yàn)镹BC模型假設(shè)屬性之間相互獨(dú)立，這個(gè)假設(shè)在實(shí)際應(yīng)用中往往是不成立的，這給NBC模型的正確分類帶來了一定影響。在屬性個(gè)數(shù)比較多或者屬性之間相關(guān)性較大時(shí)，NBC模型的分類效率比不上決策樹模型。而在屬性相關(guān)性較小時(shí)，NBC模型的性能最為良好。
接下來，我們用樸素貝葉斯在垃圾郵件過濾中的應(yīng)用來舉例說明。
2.5.1、貝葉斯垃圾郵件過濾器
問題是什么？問題是，給定一封郵件，判定它是否屬于垃圾郵件。按照先例，我們還是用 D 來表示這封郵件，注意 D 由 N 個(gè)單詞組成。我們用 h+ 來表示垃圾郵件，h- 表示正常郵件。問題可以形式化地描述為求：
P(h+|D) = P(h+) * P(D|h+) / P(D)
P(h-|D) = P(h-) * P(D|h-) / P(D)
其中 P(h+) 和 P(h-) 這兩個(gè)先驗(yàn)概率都是很容易求出來的，只需要計(jì)算一個(gè)郵件庫里面垃圾郵件和正常郵件的比例就行了。然而 P(D|h+) 卻不容易求，因?yàn)?D 里面含有 N 個(gè)單詞 d1, d2, d3, .. ，所以P(D|h+) = P(d1,d2,..,dn|h+) 。我們又一次遇到了數(shù)據(jù)稀疏性，為什么這么說呢？P(d1,d2,..,dn|h+) 就是說在垃圾郵件當(dāng)中出現(xiàn)跟我們目前這封郵件一模一樣的一封郵件的概率是多大！開玩笑，每封郵件都是不同的，世界上有無窮多封郵件。瞧，這就是數(shù)據(jù)稀疏性，因?yàn)榭梢钥隙ǖ卣f，你收集的訓(xùn)練數(shù)據(jù)庫不管里面含了多少封郵件，也不可能找出一封跟目前這封一模一樣的。結(jié)果呢？我們又該如何來計(jì)算 P(d1,d2,..,dn|h+) 呢？
我們將 P(d1,d2,..,dn|h+) 擴(kuò)展為： P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. 。熟悉這個(gè)式子嗎？這里我們會(huì)使用一個(gè)更激進(jìn)的假設(shè)，我們假設(shè) di 與 di-1 是完全條件無關(guān)的，于是式子就簡化為 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 。這個(gè)就是所謂的條件獨(dú)立假設(shè)，也正是樸素貝葉斯方法的樸素之處。而計(jì)算 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 就太簡單了，只要統(tǒng)計(jì) di 這個(gè)單詞在垃圾郵件中出現(xiàn)的頻率即可。關(guān)于貝葉斯垃圾郵件過濾更多的內(nèi)容可以參考這個(gè)條目，注意其中提到的其他資料。
2.6、層級(jí)貝葉斯模型
層級(jí)貝葉斯模型是現(xiàn)代貝葉斯方法的標(biāo)志性建筑之一。前面講的貝葉斯，都是在同一個(gè)事物層次上的各個(gè)因素之間進(jìn)行統(tǒng)計(jì)推理，然而層次貝葉斯模型在哲學(xué)上更深入了一層，將這些因素背后的因素（原因的原因，原因的原因，以此類推）囊括進(jìn)來。一個(gè)教科書例子是：如果你手頭有 N 枚硬幣，它們是同一個(gè)工廠鑄出來的，你把每一枚硬幣擲出一個(gè)結(jié)果，然后基于這 N 個(gè)結(jié)果對(duì)這 N 個(gè)硬幣的 θ （出現(xiàn)正面的比例）進(jìn)行推理。如果根據(jù)最大似然，每個(gè)硬幣的 θ 不是 1 就是 0 （這個(gè)前面提到過的），然而我們又知道每個(gè)硬幣的 p(θ) 是有一個(gè)先驗(yàn)概率的，也許是一個(gè) beta 分布。也就是說，每個(gè)硬幣的實(shí)際投擲結(jié)果 Xi 服從以 θ 為中心的正態(tài)分布，而 θ 又服從另一個(gè)以 Ψ 為中心的 beta 分布。層層因果關(guān)系就體現(xiàn)出來了。進(jìn)而 Ψ 還可能依賴于因果鏈上更上層的因素，以此類推。
第三部分、從EM算法到隱馬可夫模型（HMM）
3.1、EM 算法與基于模型的聚類
在統(tǒng)計(jì)計(jì)算中，最大期望 （EM，Expectation–Maximization）算法是在概率（probabilistic）模型中尋找參數(shù)最大似然估計(jì)的算法，其中概率模型依賴于無法觀測的隱藏變量（Latent Variabl）。最大期望經(jīng)常用在機(jī)器學(xué)習(xí)和計(jì)算機(jī)視覺的數(shù)據(jù)集聚（Data Clustering）領(lǐng)域。
通常來說，聚類是一種無指導(dǎo)的機(jī)器學(xué)習(xí)問題，如此問題描述：給你一堆數(shù)據(jù)點(diǎn)，讓你將它們最靠譜地分成一堆一堆的。聚類算法很多，不同的算法適應(yīng)于不同的問題，這里僅介紹一個(gè)基于模型的聚類，該聚類算法對(duì)數(shù)據(jù)點(diǎn)的假設(shè)是，這些數(shù)據(jù)點(diǎn)分別是圍繞 K 個(gè)核心的 K 個(gè)正態(tài)分布源所隨機(jī)生成的，使用 Han JiaWei 的《Data Ming： Concepts and Techniques》中的圖：
圖中有兩個(gè)正態(tài)分布核心，生成了大致兩堆點(diǎn)。我們的聚類算法就是需要根據(jù)給出來的那些點(diǎn)，算出這兩個(gè)正態(tài)分布的核心在什么位置，以及分布的參數(shù)是多少。這很明顯又是一個(gè)貝葉斯問題，但這次不同的是，答案是連續(xù)的且有無窮多種可能性，更糟的是，只有當(dāng)我們知道了哪些點(diǎn)屬于同一個(gè)正態(tài)分布圈的時(shí)候才能夠?qū)@個(gè)分布的參數(shù)作出靠譜的預(yù)測，現(xiàn)在兩堆點(diǎn)混在一塊我們又不知道哪些點(diǎn)屬于第一個(gè)正態(tài)分布，哪些屬于第二個(gè)。反過來，只有當(dāng)我們對(duì)分布的參數(shù)作出了靠譜的預(yù)測時(shí)候，才能知道到底哪些點(diǎn)屬于第一個(gè)分布，那些點(diǎn)屬于第二個(gè)分布。這就成了一個(gè)先有雞還是先有蛋的問題了。為了解決這個(gè)循環(huán)依賴，總有一方要先打破僵局，說，不管了，我先隨便整一個(gè)值出來，看你怎么變，然后我再根據(jù)你的變化調(diào)整我的變化，然后如此迭代著不斷互相推導(dǎo)，最終收斂到一個(gè)解。這就是 EM 算法。
EM 的意思是“Expectation-Maximazation”，在這個(gè)聚類問題里面，我們是先隨便猜一下這兩個(gè)正態(tài)分布的參數(shù)：如核心在什么地方，方差是多少。然后計(jì)算出每個(gè)數(shù)據(jù)點(diǎn)更可能屬于第一個(gè)還是第二個(gè)正態(tài)分布圈，這個(gè)是屬于 Expectation 一步。有了每個(gè)數(shù)據(jù)點(diǎn)的歸屬，我們就可以根據(jù)屬于第一個(gè)分布的數(shù)據(jù)點(diǎn)來重新評(píng)估第一個(gè)分布的參數(shù)（從蛋再回到雞），這個(gè)是 Maximazation 。如此往復(fù)，直到參數(shù)基本不再發(fā)生變化為止。這個(gè)迭代收斂過程中的貝葉斯方法在第二步，根據(jù)數(shù)據(jù)點(diǎn)求分布的參數(shù)上面。
3.2、隱馬可夫模型（HMM）
大多的書籍或論文都講不清楚這個(gè)隱馬可夫模型(HMM)，包括未鵬兄之原文也講得不夠具體明白。接下來，我盡量用直白易懂的語言闡述這個(gè)模型。然在介紹隱馬可夫模型之前，有必要先行介紹下單純的馬可夫模型(本節(jié)主要引用：統(tǒng)計(jì)自然語言處理，宗成慶編著一書上的相關(guān)內(nèi)容)。
3.2.1、馬可夫模型
我們知道，隨機(jī)過程又稱隨機(jī)函數(shù)，是隨時(shí)間而隨機(jī)變化的過程。馬可夫模型便是描述了一類重要的隨機(jī)過程。我們常常需要考察一個(gè)隨機(jī)變量序列，這些隨機(jī)變量并不是相互獨(dú)立的(注意：理解這個(gè)非相互獨(dú)立，即相互之間有千絲萬縷的聯(lián)系)。
如果此時(shí)，我也搞一大推狀態(tài)方程式，恐怕我也很難逃脫越講越復(fù)雜的怪圈了。所以，直接舉例子吧，如，一段文字中名詞、動(dòng)詞、形容詞三類詞性出現(xiàn)的情況可由三個(gè)狀態(tài)的馬爾科夫模型描述如下：
狀態(tài)s1：名詞
狀態(tài)s2：動(dòng)詞
狀態(tài)s3：形容詞
假設(shè)狀態(tài)之間的轉(zhuǎn)移矩陣如下：
s1 s2 s3
s1 0.3 0.5 0.2
A = [aij] = s2 0.5 0.3 0.2
s3 0.4 0.2 0.4
如果在該段文字中某一個(gè)句子的第一個(gè)詞為名詞，那么根據(jù)這一模型M，在該句子中這三類詞出現(xiàn)順序?yàn)镺="名動(dòng)形名”的概率為：
P(O|M)=P(s1，s2，s3，s1 | M) = P(s1) × P(s2 | s1) * P(s3 | s2)*P(s1 | s3)
=1* a12 * a23 * a31=0.5*0.2*0.4=0.004
馬爾可夫模型又可視為隨機(jī)的有限狀態(tài)機(jī)。馬爾柯夫鏈可以表示成狀態(tài)圖（轉(zhuǎn)移弧上有概率的非確定的有限狀態(tài)自動(dòng)機(jī)），如下圖所示，
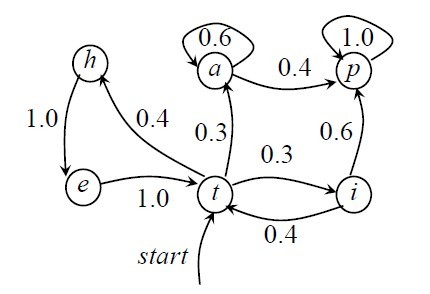
在上圖中，圓圈表示狀態(tài)，狀態(tài)之間的轉(zhuǎn)移用帶箭頭的弧表示，弧上的數(shù)字為狀態(tài)轉(zhuǎn)移的概率，初始狀態(tài)用標(biāo)記為start的輸入箭頭表示，假設(shè)任何狀態(tài)都可作為終止?fàn)顟B(tài)。圖中零概率的轉(zhuǎn)移弧省略，且每個(gè)節(jié)點(diǎn)上所有發(fā)出弧的概率之和等于1。從上圖可以看出，馬爾可夫模型可以看做是一個(gè)轉(zhuǎn)移弧上有概率的非確定的有限狀態(tài)自動(dòng)機(jī)。
3.2.2、隱馬可夫模型(HMM)
在上文介紹的馬可夫模型中，每個(gè)狀態(tài)代表了一個(gè)可觀察的事件，所以，馬可夫模型有時(shí)又稱作視馬可夫模型(VMM)，這在某種程度上限制了模型的適應(yīng)性。而在我們的隱馬可夫模型(HMM)中，我們不知道模型所經(jīng)過的狀態(tài)序列，只知道狀態(tài)的概率函數(shù)，也就是說，觀察到的事件是狀態(tài)的隨機(jī)函數(shù)，因此改模型是一個(gè)雙重的隨機(jī)過程。其中，模型的狀態(tài)轉(zhuǎn)換是不可觀察的，即隱蔽的，可觀察事件的隨機(jī)過程是隱蔽的狀態(tài)過程的隨機(jī)函數(shù)。
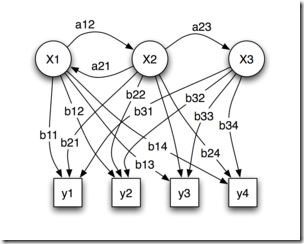
理論多說無益，接下來，留個(gè)思考題給讀者：N 個(gè)袋子，每個(gè)袋子中有M 種不同顏色的球。一實(shí)驗(yàn)員根據(jù)某一概率分布選擇一個(gè)袋子，然后根據(jù)袋子中不同顏色球的概率分布隨機(jī)取出一個(gè)球，并報(bào)告該球的顏色。對(duì)局外人：可觀察的過程是不同顏色球的序列，而袋子的序列是不可觀察的。每只袋子對(duì)應(yīng)HMM中的一個(gè)狀態(tài)；球的顏色對(duì)應(yīng)于HMM 中狀態(tài)的輸出。
3.2.2、HMM在中文分詞、機(jī)器翻譯等方面的具體應(yīng)用
隱馬可夫模型在很多方面都有著具體的應(yīng)用，如由于隱馬可夫模型HMM提供了一個(gè)可以綜合利用多種語言信息的統(tǒng)計(jì)框架，因此，我們完全可以講漢語自動(dòng)分詞與詞性標(biāo)注統(tǒng)一考察，建立基于HMM的分詞與詞性標(biāo)注的一體化系統(tǒng)。
根據(jù)上文對(duì)HMM的介紹，一個(gè)HMM通常可以看做由兩部分組成：一個(gè)是狀態(tài)轉(zhuǎn)移模型，一個(gè)是狀態(tài)到觀察序列的生成模型。具體到中文分詞這一問題中，可以把漢字串或句子S作為輸入，單詞串Sw為狀態(tài)的輸出，即觀察序列，Sw=w1w2w3...wN(N>=1)，詞性序列St為狀態(tài)序列，每個(gè)詞性標(biāo)記ct對(duì)應(yīng)HMM中的一個(gè)狀態(tài)qi，Sc=c1c2c3...cn。
那么，利用HMM處理問題問題恰好對(duì)應(yīng)于解決HMM的三個(gè)基本問題：
- 估計(jì)模型的參數(shù)；
- 對(duì)于一個(gè)給定的輸入S及其可能的輸出序列Sw和模型u=(A，B，*)，快速地計(jì)算P(Sw|u)，所有可能的Sw中使概率P(Sw|u)最大的解就是要找的分詞效果；
- 快速地選擇最優(yōu)的狀態(tài)序列或詞性序列，使其最好地解釋觀察序列。
除中文分詞方面的應(yīng)用之外，HMM還在統(tǒng)計(jì)機(jī)器翻譯中有應(yīng)用，如基于HMM的詞對(duì)位模型，更多請(qǐng)參考：統(tǒng)計(jì)自然語言處理，宗成慶編著。
參考文獻(xiàn)
- 機(jī)器學(xué)習(xí)，Tom M.Mitchhell著；
- 數(shù)據(jù)挖掘?qū)д摚?span style="font-family: 'Comic Sans MS'">[美] Pang-Ning Tan / Michael Steinbach / Vipin Kumar 著；
- 數(shù)據(jù)挖掘領(lǐng)域十大經(jīng)典算法初探；
- 數(shù)學(xué)之美番外篇：平凡而又神奇的貝葉斯方法(本文第二部分、貝葉斯分類主要來自此文)。
- http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html；
- 數(shù)學(xué)之美：http://www.google.com.hk/ggblog/googlechinablog/2006/04/blog-post_2507.html；
- 決策樹ID3分類算法的C++實(shí)現(xiàn) & yangliuy：http://blog.csdn.net/yangliuy/article/details/7322015；
- 統(tǒng)計(jì)自然語言處理，宗成慶編著；
- http://www.douban.com/note/209289903/；
- 一堆 Wikipedia 條目，一堆 paper ，《機(jī)器學(xué)習(xí)與人工智能資源導(dǎo)引》。
后記
促成自己寫這篇文章乃至整個(gè)聚類 & 分類算法系列的有3個(gè)因素，
- 一的確是如本文開頭所說，在最近參加的一些面試中被問到描述自己所知道或了解的聚類 & 分類算法(當(dāng)然，這完全不代表你將來的面試中會(huì)遇到此類問題，只是因?yàn)槲业暮啔v上寫了句：熟悉常見的聚類 & 分類算法而已)，
- 二則是之前去一家公司面試，他們有數(shù)據(jù)挖掘工程師的崗位，原來是真有那么一群人是專門負(fù)責(zé)數(shù)據(jù)分析，算法決策與調(diào)研的，情不自禁的對(duì)數(shù)據(jù)挖掘產(chǎn)生了興趣；
- 三則是手頭上有兩本這樣的經(jīng)典書籍：機(jī)器學(xué)習(xí) & 數(shù)據(jù)挖掘?qū)д摚纯从趾畏聊兀吹耐瑫r(shí)寫寫文章，做做筆記，備忘錄又有何不可呢？
(Machine Learning & Data Mining交流群：8986884；本blog算法群第23群Algorithms_23，18123186)