原文地址:http://tian0226.blog.sohu.com/142843049.html
一、墨卡托投影、高斯-克呂格投影、UTM投影
1. 墨卡托(Mercator)投影
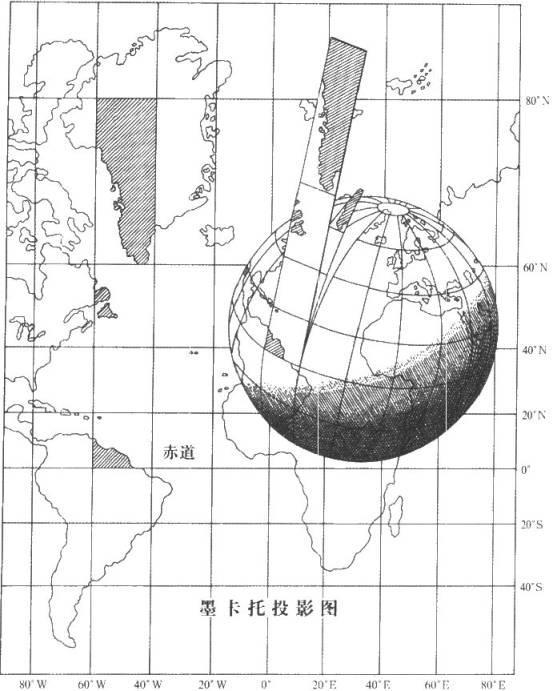
墨卡托(Mercator)投影,是一種"等角正切圓柱投影”,荷蘭地圖學家墨卡托(Gerhardus Mercator 1512-1594)在1569年擬定,假設地球被圍在一中空的圓柱里,其標準緯線與圓柱相切接觸,然后再假想地球中心有一盞燈,把球面上的圖形投影到圓柱體上,再把圓柱體展開,這就是一幅選定標準緯線上的“墨卡托投影”繪制出的地圖。墨卡托投影沒有角度變形,由每一點向各方向的長度比相等,它的經緯線都是平行直線,且相交成直角,經線間隔相等,緯線間隔從標準緯線向兩極逐漸增大。墨卡托投影的地圖上長度和面積變形明顯,但標準緯線無變形,從標準緯線向兩極變形逐漸增大,但因為它具有各個方向均等擴大的特性,保持了方向和相互位置關系的正確。在地圖上保持方向和角度的正確是墨卡托投影的優點,墨卡托投影地圖常用作航海圖和航空圖,如果循著墨卡托投影圖上兩點間的直線航行,方向不變可以一直到達目的地,因此它對船艦在航行中定位、確定航向都具有有利條件,給航海者帶來很大方便。“海底地形圖編繪規范”(GB/T 17834-1999,海軍航保部起草)中規定1:25萬及更小比例尺的海圖采用墨卡托投影,其中基本比例尺海底地形圖(1:5萬,1:25萬,1:100萬)采用統一基準緯線30°,非基本比例尺圖以制圖區域中緯為基準緯線。基準緯線取至整度或整分。
墨卡托投影坐標系取零子午線或自定義原點經線(L0)與赤道交點的投影為原點,零子午線或自定義原點經線的投影為縱坐標X軸,赤道的投影為橫坐標Y軸,構成墨卡托平面直角坐標系。
2. 高斯-克呂格(Gauss-Kruger)投影和UTM(Universal Transverse Mercator)投影
(1)高斯-克呂格投影性質
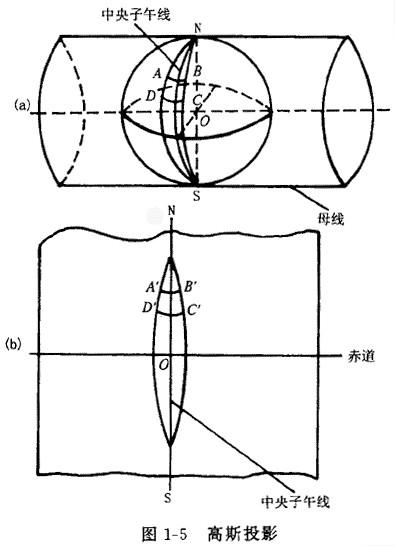
高斯-克呂格(Gauss-Kruger)投影簡稱“高斯投影”,又名"等角橫切橢圓柱投影”,地球橢球面和平面間正形投影的一種。德國數學家、物理學家、天文學家高斯(Carl FriedrichGauss,1777一 1855)于十九世紀二十年代擬定,后經德國大地測量學家克呂格(Johannes Kruger,1857~1928)于 1912年對投影公式加以補充,故名。
該投影按照投影帶中央子午線投影為直線且長度不變和赤道投影為直線的條件,確定函數的形式,從而得到高斯一克呂格投影公式。投影后,除中央子午線和赤道為直線外, 其他子午線均為對稱于中央子午線的曲線。設想用一個橢圓柱橫切于橢球面上投影帶的中央子午線,按上述投影條件,將中央子午線兩側一定經差范圍內的橢球面正形投影于橢圓柱面。將橢圓柱面沿過南北極的母線剪開展平,即為高斯投影平面。取中央子午線與赤道交點的投影為原點,中央子午線的投影為縱坐標x軸,赤道的投影為橫坐標y軸,構成高斯克呂格平面直角坐標系。
高斯-克呂格投影在長度和面積上變形很小,中央經線無變形,自中央經線向投影帶邊緣,變形逐漸增加,變形最大之處在投影帶內赤道的兩端。由于其投影精度高,變形小,而且計算簡便(各投影帶坐標一致,只要算出一個帶的數據,其他各帶都能應用),因此在大比例尺地形圖中應用,可以滿足軍事上各種需要,能在圖上進行精確的量測計算。
(2)高斯-克呂格投影分帶
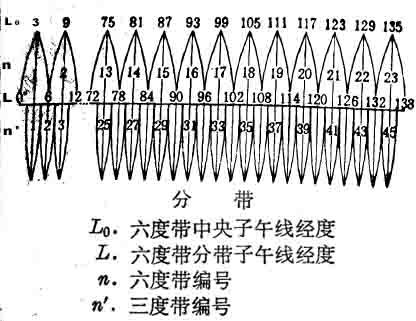
按一定經差將地球橢球面劃分成若干投影帶,這是高斯投影中限制長度變形的最有效方法。分帶時既要控制長度變形使其不大于測圖誤差,又要使帶數不致過多以減少換帶計算工作,據此原則將地球橢球面沿子午線劃分成經差相等的瓜瓣形地帶,以便分帶投影。通常按經差6度或3度分為六度帶或三度帶。六度帶自0度子午線起每隔經差6度自西向東分帶,帶號依次編為第 1、2…60帶。三度帶是在六度帶的基礎上分成的,它的中央子午線與六度帶的中央子午線和分帶子午線重合,即自 1.5度子午線起每隔經差3度自西向東分帶,帶號依次編為三度帶第 1、2…120帶。我國的經度范圍西起 73°東至135°,可分成六度帶十一個,各帶中央經線依次為75°、81°、87°、……、117°、123°、129°、135°,或三度帶二十二個。六度帶可用于中小比例尺(如 1:250000)測圖,三度帶可用于大比例尺(如 1:10000)測圖,城建坐標多采用三度帶的高斯投影。
(3)高斯-克呂格投影坐標
高斯- 克呂格投影是按分帶方法各自進行投影,故各帶坐標成獨立系統。以中央經線投影為縱軸(x), 赤道投影為橫軸(y),兩軸交點即為各帶的坐標原點。縱坐標以赤道為零起算,赤道以北為正,以南為負。我國位于北半球,縱坐標均為正值。橫坐標如以中央經線為零起算,中央經線以東為正,以西為負,橫坐標出現負值,使用不便,故規定將坐標縱軸西移500公里當作起始軸,凡是帶內的橫坐標值均加 500公里。由于高斯-克呂格投影每一個投影帶的坐標都是對本帶坐標原點的相對值,所以各帶的坐標完全相同,為了區別某一坐標系統屬于哪一帶,在橫軸坐標前加上帶號,如(4231898m,21655933m),其中21即為帶號。
(4)高斯-克呂格投影與UTM投影
某些國外的軟件如ARC/INFO或國外儀器的配套軟件如多波束的數據處理軟件等,往往不支持高斯-克呂格投影,但支持UTM投影,因此常有把UTM投影坐標當作高斯-克呂格投影坐標提交的現象。
UTM投影全稱為“通用橫軸墨卡托投影”,是等角橫軸割圓柱投影(高斯-克呂格為等角橫軸切圓柱投影),圓柱割地球于南緯80度、北緯84度兩條等高圈,該投影將地球劃分為60個投影帶,每帶經差為6度,已被許多國家作為地形圖的數學基礎。UTM投影與高斯投影的主要區別在南北格網線的比例系數上,高斯-克呂格投影的中央經線投影后保持長度不變,即比例系數為1,而UTM投影的比例系數為0.9996。UTM投影沿每一條南北格網線比例系數為常數,在東西方向則為變數,中心格網線的比例系數為0.9996,在南北縱行最寬部分的邊緣上距離中心點大約 363公里,比例系數為 1.00158。
高斯-克呂格投影與UTM投影可近似采用 Xutm=0.9996 * X高斯,Yutm=0.9996 * Y高斯進行坐標轉換。以下舉例說明(基準面為WGS84):
輸入坐標(度) 高斯投影(米) UTM投影(米) Xutm=0.9996 * X高斯, Yutm=0.9996 * Y高斯
緯度值(X)32 3543600.9 3542183.5 3543600.9*0.9996 ≈ 3542183.5
經度值(Y)121 21310996.8 311072.4 (310996.8-500000)*0.9996+500000 ≈ 311072.4
注:坐標點(32,121)位于高斯投影的21帶,高斯投影Y值21310996.8中前兩位“21”為帶號;坐標點(32,121)位于UTM投影的51帶,上表中UTM投影的Y值沒加帶號。因坐標縱軸西移了500000米,轉換時必須將Y值減去500000乘上比例因子后再加500000。
單點轉換步驟如下:
(1)選擇是高斯正轉換還是反轉換,缺省為經緯度轉換到高斯投影坐標,投影坐標單位為米。
(2)選擇大地基準面,缺省北京54,如果是GPS定位數據別忘了切換為WGS84。
(3)選擇分帶,3度或6度, 缺省為6度。
(4)輸入中央經度,20帶(114°E~120°E)中央經度為117度,21帶(120°E~126°E)中央經度為123度。
(5)如正向投影,選擇經緯度輸入數據格式,有三個選項,缺省為十進制度格式。具體輸入方式如下例:
格 式 原始緯度值 原始經度值 輸入緯度值 輸入經度值
十進制度 35.445901° 122.997344° 35.445901 122.997344
度分 35°26.7541′ 122°59.8406′ 3526.7541 12259.8406
度分秒 35°26′45.245″ 122°59′50.438″ 352645.245 1225950.438
(6)正投影按選定格式在“輸入”欄輸入經緯度值,反投影輸入以米為單位的X、Y坐標值。
(7)單擊“單點轉換”按鈕。
(8)在“輸出”欄查看計算結果。
批量轉換步驟如下:
(1)準備好需要轉換的輸入數據文件,要求是文本文件,分兩列,第一列緯度值或縱向坐標值,第二列經度值或橫向坐標值,兩列之間用空格分開。正向投影時,緯度值及經度值格式可以有三種選擇,缺省當作十進制度處理;反向投影時,縱向及橫向坐標值必須以米為單位。
下例為度分秒格式(WGS84)的6°帶正投影輸入數據文件 testdata.txt
352645.245 1225950.438
353800.402 1230000.378
351600.519 1225959.506
345800.101 1225959.8
343600.336 1230000.26
341400.018 1225959.897
335159.17 1225959.46
333000.08 1230000.28
(2)選擇是高斯正轉換還是反轉換,缺省為經緯度轉換到高斯投影坐標,投影坐標單位為米。
(3)選擇大地基準面,缺省北京54,如果是GPS定位數據別忘了切換為WGS84。
(4)選擇分帶,3度或6度, 缺省為6度。
(5)輸入中央經度,20帶(114°E~120°E)中央經度為117度,21帶(120°E~126°E)中央經度為123度。
(6)如正向投影,選擇輸入數據文件中的經緯度輸入數據格式,有三個選項,缺省為十進制度格式。
(7)單擊“批量轉換”按鈕。彈出打開文件對話框,輸入你的數據文件名。
(8)輸入轉換結果文件名,單擊“保存”后,程序開始進行計算。
(9)打開輸出文件查看計算結果,結果分五列,第一序號,第二列輸入緯度值或縱向坐標值,第三列輸入經度值或橫向坐標值,第四列轉換后緯度值或縱向坐標值,第五列轉換后經度值或橫向坐標值。
下例為度分秒格式(WGS84)的6°帶正投影轉換結果數據文件 result.txt
1 352645.245 1225950.438 3924063.3 21499758.9
2 353800.402 1230000.378 3944871.4 21500009.5
3 351600.519 1225959.506 3904193.8 21499987.5
4 345800.101 1225959.8 3870898.1 21499994.9
5 343600.336 1230000.26 3830228.5 21500006.6
6 341400.018 1225959.897 3789544.4 21499997.4
7 335159.17 1225959.46 3748846.4 21499986.1
8 333000.08 1230000.28 3708205 21500007.2
二、分帶方法
我國采用6度分帶和3度分帶:
1∶2.5萬及1∶5萬的地形圖采用6度分帶投影,即經差為6度,從零度子午線開始,自西向東每個經差6度為一投影帶,全球共分60個帶,用1,2,3,4,5,……表示.即東經0~6度為第一帶,其中央經線的經度為東經3度,東經6~12度為第二帶,其中央經線的經度為9度。
1∶1萬的地形圖采用3度分帶,從東經1.5度的經線開始,每隔3度為一帶,用1,2,3,……表示,全球共劃分120個投影帶,即東經1.5~ 4.5度為第1帶,其中央經線的經度為東經3度,東經4.5~7.5度為第2帶,其中央經線的經度為東經6度.我省位于東經113度-東經120度之間,跨第38、39、40共計3個帶,其中東經115.5度以西為第38帶,其中央經線為東經114度;東經115.5~118.5度為39帶,其中央經線為東經117度;東經118.5度以東到山海關為40帶,其中央經線為東經120度。地形圖上公里網橫坐標前2位就是帶號,例如:1∶5萬地形圖上的橫坐標為20345486,其中20即為帶號,345486為橫坐標值。2.當地中央經線經度的計算六度帶中央經線經度的計算:當地中央經線經度=6°×當地帶號-3°,例如:地形圖上的橫坐標為20345,其所處的六度帶的中央經線經度為:6°×20-3°=117°(適用于1∶2.5萬和1∶5萬地形圖)。三度帶中央經線經度的計算:中央經線經度=3°×當地帶號(適用于1∶1萬地形圖)。