Waterloo Local 2001.09.29 && 2002.01.26 && 2002.07.01
Posted on 2009-02-13 19:36 hello_world 閱讀(1854) 評論(0) 編輯 收藏 引用| 題目分類 |
|
| Adventures in Moving - Part IV | DP |
| Pairsumonious Numbers | 搜索 |
| Snow Clearing | 簡單題 |
| Stack 'em Up | 模擬 |
Adventures in Moving - Part IV:
這題DP的階段和決策都非常明顯。g[i][j]=min( g[i-1][j+dis[i]-dis[i-1]-buy]+buy*pirce[i] )
g[i][j]表示將要離開第i個加油站時,有j升汽油,所要花費的最少的錢。
Pairsumonious Numbers :
首先 n==3 時很容易求出答案,a1+a2, a1+a3, a2+a3,兩兩相加再減去另一個
然后 n > 3 時首先我們排序,有順序就是成功的一半,
如果那 n 個數(shù)的大小是 a1 < a2 < a3 < ... < an
那么最小的是 a1+a2, 次小的是 a1+a3,如果我們知道 a2+a3 在哪 那該多好啊
幸運的是 a2+a3只可能出現(xiàn)在第 3 位到第 n 位之間,n又是小于10的數(shù),那我們只要枚舉
每種情況就可以了
這樣我們就能求出a1 , a2, a3 那對解題有什么用呢?
這時我們把 a1+a2, a1+a3, a2+a3 刪掉,剩下的最小的是不是肯定只有 a1+a4,那是不是
a4也求出來了
接著我們把 a1+a4, a2+a4, a3+a4都刪掉,剩下最小的不就是 a1+a5了嗎
不斷進行上述過程就能求出答案
至于有相同元素的時候,很容易就知道也符合上述做法,正因為有相同元素,中間可用multiset
實現(xiàn)上述功能
Snow Clearing:
只需要把每條街加起來再乘以2就是總的距離,除以速度然后化成時間即可!
Stack 'em Up:
這題只要把題意看懂之后,就沒問題了。首先給你n種洗牌策略,然后再給你若干個k,在前一次洗好的牌的基礎上,按照第k種洗牌策略洗。每洗一次,輸出目前的牌的順序。
Waterloo Local 2002.01.26
Discrete Logging :
求以b為基模于n的離散對數(shù)我們有O(n^0.5*logn)的算法
有興趣者可查看Shank's Baby-Step-Gaint-Step Algorithm
A Star not a Tree? :
給你平面上 n ( n < 100)個點, 要求一個點p,使得 p 到各個點的距離之和最小
用牛頓迭代,能證明x,y偏導為0時,有最小值,但我不會證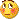 (回去學高數(shù))
(回去學高數(shù))
既然知道方程x,y偏導為0時有最小值,那就好辦了,取平均值為初值,然后不斷迭代,
但我精度調到 1e-4 才能過,這樣我的迭代跑了300ms,別人都跑0ms,總感覺有問題
貼出迭代代碼,希望大家給我指正
Waterloo local 2002.07.01
| 題目分類 |
|
| Discrete Logging | 求離散對數(shù) |
| Hardwood Species | 簡單題 |
| Forests |
水題(stl運用) |
| A Star not a Tree? | 牛頓迭代法 |
Discrete Logging :
求以b為基模于n的離散對數(shù)我們有O(n^0.5*logn)的算法
有興趣者可查看Shank's Baby-Step-Gaint-Step Algorithm
A Star not a Tree? :
給你平面上 n ( n < 100)個點, 要求一個點p,使得 p 到各個點的距離之和最小
用牛頓迭代,能證明x,y偏導為0時,有最小值,但我不會證
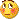 (回去學高數(shù))
(回去學高數(shù))既然知道方程x,y偏導為0時有最小值,那就好辦了,取平均值為初值,然后不斷迭代,
但我精度調到 1e-4 才能過,這樣我的迭代跑了300ms,別人都跑0ms,總感覺有問題
貼出迭代代碼,希望大家給我指正
while( !( zero(x1 - x0) && zero(y1 - y0) ) )
{
x0=x1, y0=y1;
for( fx=0, i=0; i < n; i++)
fx+= (x0 - p[i][0])/ sqrt( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
for(fxx=0, i =0; i < n; i++)
fxx+=( 2*(x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) ) / ( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
x1 = x0 - fx/fxx;
for(fy=0, i=0; i < n; i++)
fy+=(y0 - p[i][1])/ sqrt( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
for(fyy=0, i=0; i < n; i++)
fyy+=( (x0 - p[i][0])*(x0 - p[i][0]) + 2*(y0 - p[i][1])*(y0 - p[i][1]) ) / ( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
y1=y0 - fy/fyy;
}
{
x0=x1, y0=y1;
for( fx=0, i=0; i < n; i++)
fx+= (x0 - p[i][0])/ sqrt( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
for(fxx=0, i =0; i < n; i++)
fxx+=( 2*(x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) ) / ( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
x1 = x0 - fx/fxx;
for(fy=0, i=0; i < n; i++)
fy+=(y0 - p[i][1])/ sqrt( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
for(fyy=0, i=0; i < n; i++)
fyy+=( (x0 - p[i][0])*(x0 - p[i][0]) + 2*(y0 - p[i][1])*(y0 - p[i][1]) ) / ( (x0 - p[i][0])*(x0 - p[i][0]) + (y0 - p[i][1])*(y0 - p[i][1]) );
y1=y0 - fy/fyy;
}
Waterloo local 2002.07.01
| 題目分類 |
|
| Hay Points | 簡單題 |
| Jogging Trails | 圖論,中國郵路問題 |
| Beavergnaw | 簡單題 |
| Power Strings | 水題 |
| Relatives |
歐拉函數(shù) |
Jogging Trails:
題目意思是給定一些點,然后一些邊,并且兩個點之間可能有多條邊,問從一個點出發(fā),遍歷完所有的邊至少一次且最后在回到出發(fā)點需要走的最少距離!
如果這個圖是歐拉圖,那么距離就是邊之和,一個圖存在歐拉圖的充要條件是每個定點的度為偶數(shù)!
但是如果不是歐拉圖,那么我們就要把這個圖變成歐拉圖,只需要添加一些邊,頂點的度全部為偶數(shù)就好了,因為一個圖中奇數(shù)度頂點一定有偶數(shù)個!所以只要枚舉這樣的奇數(shù)度頂點,添加邊使其度為偶數(shù),很明顯添加的邊不會影響其他偶數(shù)度頂點的奇偶性!并且由于要距離最小,所以添加的邊一定是這兩個頂點的最短距離!這一步可以用記憶化搜索實現(xiàn)!
歐拉函數(shù)的一些題目(
轉http://hi.baidu.com/wuxyy/blog/item/33957f1ee03a1cf51bd5761d.html
)
題目意思是給定一些點,然后一些邊,并且兩個點之間可能有多條邊,問從一個點出發(fā),遍歷完所有的邊至少一次且最后在回到出發(fā)點需要走的最少距離!
如果這個圖是歐拉圖,那么距離就是邊之和,一個圖存在歐拉圖的充要條件是每個定點的度為偶數(shù)!
但是如果不是歐拉圖,那么我們就要把這個圖變成歐拉圖,只需要添加一些邊,頂點的度全部為偶數(shù)就好了,因為一個圖中奇數(shù)度頂點一定有偶數(shù)個!所以只要枚舉這樣的奇數(shù)度頂點,添加邊使其度為偶數(shù),很明顯添加的邊不會影響其他偶數(shù)度頂點的奇偶性!并且由于要距離最小,所以添加的邊一定是這兩個頂點的最短距離!這一步可以用記憶化搜索實現(xiàn)!
歐拉函數(shù)的一些題目(
轉http://hi.baidu.com/wuxyy/blog/item/33957f1ee03a1cf51bd5761d.html
)
歐拉函數(shù)入門題目:poj3090 Visible Lattice Points poj2407 Relatives
poj2478 Farey Sequence
歐拉函數(shù)高級應用:poj2480 Longge's problem poj1091 跳蚤



