來吧，朋友!

讓我再一次比較完整的重復一下我們要解決的問題：我們有屬于兩個類別的樣本點（并不限定這些點在二維空間中）若干，如圖，

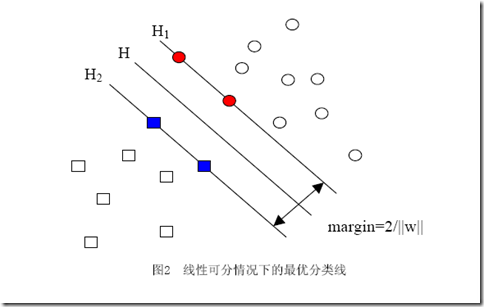
圓形的樣本點定為正樣本（連帶著，我們可以把正樣本所屬的類叫做正類），方形的點定為負例。我們想求得這樣一個線性函數（在n維空間中的線性函數）：

g(x)=wx+b

使得所有屬于正類的點x₊代入以后有g(x₊)≥1，而所有屬于負類的點x_-代入后有g(x_-)≤-1（之所以總跟1比較，無論正一還是負一，都是因為我們固定了間隔為1，注意間隔和幾何間隔的區別）。代入g(x)后的值如果在1和-1之間，我們就拒絕判斷。

求這樣的g(x)的過程就是求w（一個n維向量）和b（一個實數）兩個參數的過程（但實際上只需要求w，求得以后找某些樣本點代入就可以求得b）。因此在求g(x)的時候，w才是變量。

你肯定能看出來，一旦求出了w（也就求出了b），那么中間的直線H就知道了（因為它就是wx+b=0嘛，哈哈），那么H1和H2也就知道了（因為三者是平行的，而且相隔的距離還是||w||決定的）。那么w是誰決定的？顯然是你給的樣本決定的，一旦你在空間中給出了那些個樣本點，三條直線的位置實際上就唯一確定了（因為我們求的是最優的那三條，當然是唯一的），我們解優化問題的過程也只不過是把這個確定了的東西算出來而已。

樣本確定了w，用數學的語言描述，就是w可以表示為樣本的某種組合：

w=α₁x₁+α₂x₂+…+α_nx_n

式子中的α_i是一個一個的數（在嚴格的證明過程中，這些α被稱為拉格朗日乘子），而x_i是樣本點，因而是向量，n就是總樣本點的個數。為了方便描述，以下開始嚴格區別數字與向量的乘積和向量間的乘積，我會用α₁x₁表示數字和向量的乘積，而用<x₁,x₂>表示向量x₁,x₂的內積（也叫點積，注意與向量叉積的區別）。因此g(x)的表達式嚴格的形式應該是：

g(x)=<w,x>+b

但是上面的式子還不夠好，你回頭看看圖中正樣本和負樣本的位置，想像一下，我不動所有點的位置，而只是把其中一個正樣本點定為負樣本點（也就是把一個點的形狀從圓形變為方形），結果怎么樣？三條直線都必須移動（因為對這三條直線的要求是必須把方形和圓形的點正確分開）！這說明w不僅跟樣本點的位置有關，還跟樣本的類別有關（也就是和樣本的“標簽”有關）。因此用下面這個式子表示才算完整：

w=α₁y₁x₁+α₂y₂x₂+…+α_ny_nx_n （式1）

其中的y_i就是第i個樣本的標簽，它等于1或者-1。其實以上式子的那一堆拉格朗日乘子中，只有很少的一部分不等于0（不等于0才對w起決定作用），這部分不等于0的拉格朗日乘子后面所乘的樣本點，其實都落在H1和H2上，也正是這部分樣本（而不需要全部樣本）唯一的確定了分類函數，當然，更嚴格的說，這些樣本的一部分就可以確定，因為例如確定一條直線，只需要兩個點就可以，即便有三五個都落在上面，我們也不是全都需要。這部分我們真正需要的樣本點，就叫做支持（撐）向量！（名字還挺形象吧，他們“撐”起了分界線）

式子也可以用求和符號簡寫一下：

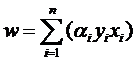
因此原來的g(x)表達式可以寫為：

注意式子中x才是變量，也就是你要分類哪篇文檔，就把該文檔的向量表示代入到 x的位置，而所有的x_i統統都是已知的樣本。還注意到式子中只有x_i和x是向量，因此一部分可以從內積符號中拿出來，得到g(x)的式子為：

發現了什么？w不見啦！從求w變成了求α。

但肯定有人會說，這并沒有把原問題簡化呀。嘿嘿，其實簡化了，只不過在你看不見的地方，以這樣的形式描述問題以后，我們的優化問題少了很大一部分不等式約束（記得這是我們解不了極值問題的萬惡之源）。但是接下來先跳過線性分類器求解的部分，來看看 SVM在線性分類器上所做的重大改進——核函數。

生存？還是毀滅？——哈姆雷特

可分？還是不可分？——支持向量機

之前一直在討論的線性分類器,器如其名（汗，這是什么說法啊），只能對線性可分的樣本做處理。如果提供的樣本線性不可分，結果很簡單，線性分類器的求解程序會無限循環，永遠也解不出來。這必然使得它的適用范圍大大縮小，而它的很多優點我們實在不原意放棄，怎么辦呢？是否有某種方法，讓線性不可分的數據變得線性可分呢？

有！其思想說來也簡單，來用一個二維平面中的分類問題作例子，你一看就會明白。事先聲明，下面這個例子是網絡早就有的，我一時找不到原作者的正確信息，在此借用，并加進了我自己的解說而已。

例子是下面這張圖：

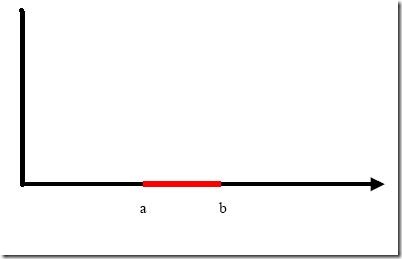
我們把橫軸上端點a和b之間紅色部分里的所有點定為正類，兩邊的黑色部分里的點定為負類。試問能找到一個線性函數把兩類正確分開么？不能，因為二維空間里的線性函數就是指直線，顯然找不到符合條件的直線。

但我們可以找到一條曲線，例如下面這一條：

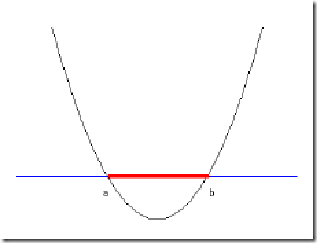
顯然通過點在這條曲線的上方還是下方就可以判斷點所屬的類別（你在橫軸上隨便找一點，算算這一點的函數值，會發現負類的點函數值一定比0大，而正類的一定比0小）。這條曲線就是我們熟知的二次曲線，它的函數表達式可以寫為：

問題只是它不是一個線性函數，但是，下面要注意看了，新建一個向量y和a：

這樣g(x)就可以轉化為f(y)=<a,y>，你可以把y和a分別回帶一下，看看等不等于原來的g(x)。用內積的形式寫你可能看不太清楚，實際上f(y)的形式就是：

g(x)=f(y)=ay

在任意維度的空間中，這種形式的函數都是一個線性函數（只不過其中的a和y都是多維向量罷了），因為自變量y的次數不大于1。

看出妙在哪了么？原來在二維空間中一個線性不可分的問題，映射到四維空間后，變成了線性可分的！因此這也形成了我們最初想解決線性不可分問題的基本思路——向高維空間轉化，使其變得線性可分。

而轉化最關鍵的部分就在于找到x到y的映射方法。遺憾的是，如何找到這個映射，沒有系統性的方法（也就是說，純靠猜和湊）。具體到我們的文本分類問題，文本被表示為上千維的向量，即使維數已經如此之高，也常常是線性不可分的，還要向更高的空間轉化。其中的難度可想而知。

小Tips:為什么說f(y)=ay是四維空間里的函數?

大家可能一時沒看明白。回想一下我們二維空間里的函數定義
  g(x)=ax+b
變量x是一維的，為什么說它是二維空間里的函數呢？因為還有一個變量我們沒寫出來，它的完整形式其實是
  y=g(x)=ax+b
即
  y=ax+b
看看，有幾個變量？兩個。那是幾維空間的函數？（作者五歲的弟弟答：五維的。作者：……）
再看看
f(y)=ay
里面的y是三維的變量，那f(y)是幾維空間里的函數？（作者五歲的弟弟答：還是五維的。作者：……）

用一個具體文本分類的例子來看看這種向高維空間映射從而分類的方法如何運作，想象一下，我們文本分類問題的原始空間是1000維的（即每個要被分類的文檔被表示為一個1000維的向量），在這個維度上問題是線性不可分的。現在我們有一個2000維空間里的線性函數

f(x^’)=<w^’,x^’>+b

注意向量的右上角有個 ’哦。它能夠將原問題變得可分。式中的 w^’和x^’都是2000維的向量，只不過w^’是定值，而x^’是變量（好吧,嚴格說來這個函數是2001維的,哈哈），現在我們的輸入呢，是一個1000維的向量x，分類的過程是先把x變換為2000維的向量x^’，然后求這個變換后的向量x^’與向量w^’的內積，再把這個內積的值和b相加，就得到了結果，看結果大于閾值還是小于閾值就得到了分類結果。

你發現了什么？我們其實只關心那個高維空間里內積的值，那個值算出來了，分類結果就算出來了。而從理論上說， x^’是經由x變換來的，因此廣義上可以把它叫做x的函數（有一個x，就確定了一個x^’，對吧，確定不出第二個），而w^’是常量，它是一個低維空間里的常量w經過變換得到的，所以給了一個w 和x的值，就有一個確定的f(x^’)值與其對應。這讓我們幻想，是否能有這樣一種函數K(w,x),他接受低維空間的輸入值，卻能算出高維空間的內積值<w^’,x^’>？

如果有這樣的函數，那么當給了一個低維空間的輸入x以后，

g(x)=K(w,x)+b

f(x^’)=<w^’,x^’>+b

這兩個函數的計算結果就完全一樣，我們也就用不著費力找那個映射關系，直接拿低維的輸入往g(x)里面代就可以了（再次提醒，這回的g(x)就不是線性函數啦，因為你不能保證K(w,x)這個表達式里的x次數不高于1哦）。

萬幸的是，這樣的K(w,x)確實存在（發現凡是我們人類能解決的問題，大都是巧得不能再巧，特殊得不能再特殊的問題，總是恰好有些能投機取巧的地方才能解決，由此感到人類的渺小），它被稱作核函數（核，kernel），而且還不止一個，事實上，只要是滿足了Mercer條件的函數，都可以作為核函數。核函數的基本作用就是接受兩個低維空間里的向量，能夠計算出經過某個變換后在高維空間里的向量內積值。幾個比較常用的核函數，俄，教課書里都列過，我就不敲了（懶！）。

回想我們上節說的求一個線性分類器，它的形式應該是：

現在這個就是高維空間里的線性函數（為了區別低維和高維空間里的函數和向量，我改了函數的名字，并且給w和x都加上了 ’），我們就可以用一個低維空間里的函數（再一次的，這個低維空間里的函數就不再是線性的啦）來代替，

又發現什么了？f(x’) 和g(x)里的α，y，b全都是一樣一樣的！這就是說，盡管給的問題是線性不可分的，但是我們就硬當它是線性問題來求解，只不過求解過程中，凡是要求內積的時候就用你選定的核函數來算。這樣求出來的α再和你選定的核函數一組合，就得到分類器啦！

明白了以上這些，會自然的問接下來兩個問題：

1． 既然有很多的核函數，針對具體問題該怎么選擇？

2． 如果使用核函數向高維空間映射后，問題仍然是線性不可分的，那怎么辦？

第一個問題現在就可以回答你：對核函數的選擇，現在還缺乏指導原則！各種實驗的觀察結果（不光是文本分類）的確表明，某些問題用某些核函數效果很好，用另一些就很差，但是一般來講，徑向基核函數是不會出太大偏差的一種，首選。（我做文本分類系統的時候，使用徑向基核函數，沒有參數調優的情況下，絕大部分類別的準確和召回都在85%以上，可見。雖然libSVM的作者林智仁認為文本分類用線性核函數效果更佳，待考證）

對第二個問題的解決則引出了我們下一節的主題：松弛變量。