1. 遺傳算法的數據結構大致畫了下數據結構的邏輯圖，如下：
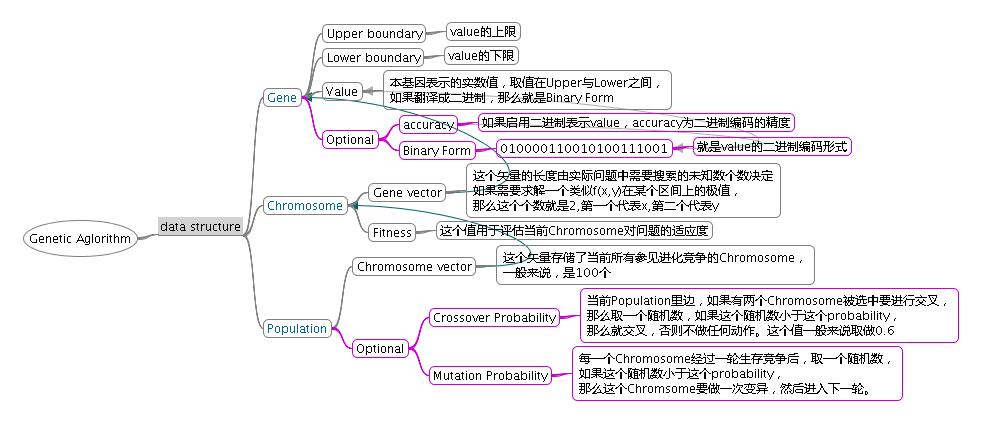
參加生存競爭的整個群體稱為種群(Population)，種群中所有參與進化的個體(Chromosome)的數量一般為一個定值，而每個個體可能含有多于一個基因(Gene)。
例如，求解一個Camel函數在區間-100<x,y<100上邊的最小值:
f(x,y)=[4 - 2.1(x^2) + (x^3)/3](x^2) + xy +[-4 +4(y^2)](y^2)
這時候就需要兩個基因，每個基因上限是100,下限是-100.
假設數值求解的精度為10^(-7)，那么對應的二進制編碼長度N可以這樣確定
(2^N)-1 >= [ 100 - ( -100 ) ] / [ 10^(-7) ]
于是，將一個十進制數字x轉化為二進制
x' = [x- (-100)] * [(2^N) -1] / [ 100 - ( -100 ) ]
同樣，也可以將一個二進制數字x'轉化為十進制數字x
程序中，數據結構可以這樣定義
1 struct Gene
2 {
3 long double Upper; //upper boundary of the value
4 long double Lower; //lower boundary of the value
5 long double Value; //decimal value of the gene
6 std :: vector< int > Binary_Array; //binary form of the value
7 long double Accuracy; //accuracy of the value
8 };
9
10 struct Chromosome
11 {
12 std :: vector< Gene > Gene_Array; //Gene[]
13 long double Fitness; //the weigh of the chromosome in ga
14 };
15
16 struct Population
17 {
18 std :: vector< Chromosome > Chromosome_Array; //Chromosome[]
19
20 long double Mutation_Probability; //probability of mutation
21 long double Crossover_Probability; //probability of crossover
22 };
2. 與數據結構相關的基本算法1） 基因的自動初始化 --在搜索區間中隨機生成初始基因
1 //generate random value
2 void initialize( Gene& g)
3 {
4 const long double Ran = ran();
5 const long double Upper = g.Upper;
6 const long double Lower = g.Lower;
7 //const long double Accuracy = g.Accuracy;
8 assert( Upper > Lower );
9
10 g.Value = Lower + Ran * ( Upper - Lower );
11 }
12
2） 基因的二進制編碼--將十進制數據編碼為二進制
1 //decimal value -> binary form
2 void encoding( Gene& g )
3 {
4 const long double Value = g.Value;
5 const long double Upper = g.Upper;
6 const long double Lower = g.Lower;
7 const long double Accuracy = g.Accuracy;
8
9 unsigned int Size = 1 +
10 static_cast< unsigned int >
11 (
12 log( ( Upper - Lower ) / ( Accuracy ) ) /
13 log( 2.0 )
14 );
15
16 if ( Size > 63 )
17 Size = 63;
18
19 const unsigned long long Max = 1 << Size;
20
21 unsigned long long x =
22 static_cast< unsigned long long >
23 (
24 static_cast< long double>( Max -1 ) *
25 ( Value - Lower ) /
26 ( Upper - Lower )
27 );
28
29 std :: vector<int> Binary_Array;
30
31 for ( unsigned int i = 0; i <= Size; ++i )
32 {
33 if ( x & 1 ) //case odd
34 {
35 Binary_Array.push_back( 1 );
36 }
37 else //case even
38 {
39 Binary_Array.push_back( 0 );
40 }
41 x >>= 1;
42 }
43
44 g.Binary_Array = Binary_Array;
45
46 }
47
3）二進制向十進制的解碼--將二進制數據解碼為十進制
1 //binary form -> decimal value
2 void decoding( Gene& g )
3 {
4 const unsigned int Size = g.Binary_Array.size();
5 assert( Size > 0 );
6
7 const long double Upper = g.Upper;
8 const long double Lower = g.Lower;
9 //const long double Accuracy = g.Accuracy;
10 const std::vector<int> Binary_Array = g.Binary_Array;
11
12 const unsigned long long Max = 1 << Size;
13 unsigned long long x = 0;
14
15 for( unsigned int i = Size; i > 0; --i )
16 {
17 x += Binary_Array[i-1];
18 x <<= 1;
19 }
20 //x += Binary_Array[0];
21
22 const long double Value = Lower +
23 static_cast<long double>( x ) /
24 static_cast<long double>( Max - 1 ) *
25 ( Upper - Lower );
26
27 g.Value = Value;
28 }
4）普通二進制編碼轉到格雷碼
多說一點，在進行二進制交叉的時候，使用格雷碼比普通的二進制編碼要有效一點。
例如，如果采用普通二進制編碼，8可以表示為1000，而7則表示為0111，四個位都是不同的，7與8僅僅相差了1，但是普通二進制編碼卻相差了這么多，如果對他們進行交叉的話，出來的結果偏離7與8實在太遠了，而使用格雷碼則可以避免這種尷尬。
這里（http://baike.baidu.com/view/358724.htm）是百度一個有關格雷碼的介紹，我就不復制了，有興趣的話過去看看。
1 //Normal Binary Form --> Gray Binary Form
2 void normal2gray( Gene& g )
3 {
4 const unsigned int Size = g.Binary_Array.size();
5 assert( Size > 0 );
6
7 std :: vector<int> G_Binary_Array; //gray code
8 const std :: vector<int> Binary_Array = g.Binary_Array;
9
10 G_Binary_Array.push_back( Binary_Array[0] );
11 for ( unsigned int i = 1; i < Size; ++i )
12 {
13 G_Binary_Array.push_back( ( Binary_Array[i-1] + Binary_Array[i] ) & 1 );
14 }
15 g.Binary_Array = G_Binary_Array;
16 }
17
5） 格雷碼轉換到普通二進制編碼
1 //Gray Binary Form --> Normal Binary Form
2 void normal2binary( Gene& g )
3 {
4 const unsigned int Size = g.Binary_Array.size();
5 assert( Size > 0 );
6
7 std :: vector<int> N_Binary_Array; //Normal Binary Form
8 const std :: vector<int> Binary_Array = g.Binary_Array;
9
10 unsigned int result = 0;
11 for ( unsigned int i = 0; i < Size; ++i )
12 {
13 result += Binary_Array[i];
14 N_Binary_Array.push_back( result & 1 );
15 }
16
17 g.Binary_Array = N_Binary_Array;
18 }
19
20
6） 進化種群初始化函數一 -- 生成進化個體
1 void initialize( Population& population,
2 const unsigned int size
3 )
4 {
5 Chromosome* chromosome = new Chromosome;
6
7 population.Generation = 1;
8
9 for ( unsigned int i = 0; i < size; ++i )
10 {
11
12 population.Chromosome_Array.push_back( *chromosome );
13 }
14
15 delete chromosome;
16 }
17
7） 進化種群初始化函數二 -- 對種群中的每個個體，初始化其基因
如上邊的Camel函數，因為里邊有兩個自變量需要搜索，那么需要調用這個函數兩次，分別對應于x和y
append_gene( p, 100, -100, 1E-7);
append_gene( p, 100, -100, 1E-7);
1 void append_gene( Population& population,
2 const long double& upper,
3 const long double& lower,
4 const long double& accuracy
5 )
6 {
7 assert( upper > lower );
8 assert( accuracy > 0 );
9
10 Gene* gene = new Gene;
11
12 gene -> Upper = upper;
13 gene -> Lower = lower;
14 gene -> Accuracy = accuracy;
15
16 const unsigned int Size = population.Chromosome_Array.size();
17 for ( unsigned int i = 0; i < Size; ++i )
18 {
19 initialize( *gene );
20 population.Chromosome_Array[i].Gene_Array.push_back( *gene );
21 }
22
23 delete gene;
24 }
25
8） 搜尋最佳適應度個體 -- 進化到指定年代后，找出最佳個體
1 const std :: vector< long double > elite( const Population& population )
2 {
3 const unsigned int Size = population.Chromosome_Array.size();
4 assert( Size > 0 );
5 long double max = population.Chromosome_Array[0].Fitness;
6 unsigned int index = 0;
7 for ( unsigned int i = 1; i < Size; ++i )
8 {
9 if ( population.Chromosome_Array[i].Fitness > max )
10 {
11 index = i;
12 max = population.Chromosome_Array[i].Fitness;
13 }
14 }
15
16 std :: vector<long double> Elite;
17 const unsigned int G_Size = population.Chromosome_Array[0].Gene_Array.size();
18 for ( unsigned int i = 0; i < G_Size; ++i )
19 Elite.push_back( population.Chromosome_Array[index].Gene_Array[i].Value );
20
21 return Elite;
22 }
9） 隨機函數
由于遺傳算法是一種隨機搜索算法，執行的時候需要大量的隨機數（記得之前搜索四個未知數，種群100個體，進化800代，大概整個運行過程用了10^10數量級的隨機數），庫里的隨機數生成函數肯定不行。當前使用了一個Kruth推薦的（Kruth, D. E. 1997, Seminumerical Algorithms, vol2. $3）、基于相減方法的隨機數生成算法，比基于線性同余方法的快一點。
1 #include <ctime>
2
3 static long double _ran( int& seed );
4
5 long double ran()
6 {
7 static int seed = static_cast < unsigned int >( time( NULL ) );
8 return _ran( seed );
9 }
10
11 static long double _ran( int& seed )
12 {
13
14 const int MBIG = 1000000000;
15 const int MSEED = 161803398;
16 const int MZ = 0;
17 const long double FAC = 1.0E-9L;
18
19 static int inext, inextp;
20 static long ma[56];
21 static int iff = 0;
22 long mj, mk;
23 int i, ii, k;
24
25 if ( seed < 0 || iff == 0)
26 {
27 iff = 1;
28 mj = MSEED - (seed < 0 ? -seed : seed);
29 mj %= MBIG;
30 ma[55] = mj;
31 mk = 1;
32 for (i = 1; i <= 54; i++) {
33 ii = (21 * i) % 55;
34 ma[ii] = mk;
35 mk = mj - mk;
36 if (mk < MZ)
37 mk += MBIG;
38 mj = ma[ii];
39 }
40 for (k = 1; k <= 4; k++)
41 for (i = 1; i <= 55; i++)
42 {
43 ma[i] -= ma[1 + (i + 30) % 55];
44 if (ma[i] < MZ)
45 ma[i] += MBIG;
46 }
47 inext = 0;
48 inextp = 31;
49 seed = 1;
50 }
51 if (++inext == 56)
52 inext = 1;
53 if (++inextp == 56)
54 inextp = 1;
55 mj = ma[inext] - ma[inextp];
56 if (mj < MZ)
57 mj += MBIG;
58 ma[inext] = mj;
59 return mj * FAC;
60 }
61
62
posted on 2008-06-16 16:53
Wang Feng 閱讀(2919)
評論(0) 編輯 收藏 引用 所屬分類:
Numerical C++