前天晚上檢查LAC代碼,總覺得其使用的'記憶'算法有問題,調(diào)試很久,火起,重新實現(xiàn)了一個...
所謂'記憶'算法,最著名的應該是那個什么'艾賓浩斯記憶曲線'了,可惜咱數(shù)學不好,沒看懂,只好自己弄個簡單的了...
'記憶'算法由四個參數(shù)組合而成,很簡單 -- 一個
時間間隔參數(shù)乘以由
前次分數(shù),
本次分數(shù)以及
結(jié)果判定確定的三維坐標,即可獲得
下次時間.
三維坐標系如下:
float rateTable[4][4] = {
{ 1.75f, 0.80f, 0.45f, 0.17f },
{ 1.50f, 1.25f, 0.55f, 0.20f },
{ 1.00f, 0.80f, 0.45f, 0.20f },
{ 0.80f, 0.50f, 0.30f, 0.17f }
};
int judgeTable[2][4] = {
{ 0, 1, 1, 2 },
{ 2, 2, 3, 3 }
};
計算方法簡化如下:
check = judgeTable[judge][preScore];
next = ((last != 0) ? (updated - last) : 7) * rateTable[curScore][check] + updated + 1;
咱也不知道這個算法好不好,所有系數(shù)完全自己推倒杜撰的(該不該弄個專利去呢...),為了表達自己對'嚴謹科學態(tài)度'的敬意,做了如下測試,請看各位報表..
1. 假定某個單詞從第一次就選擇'認識',且判定為'正確'(意思是自己判定'認識'此單詞的判斷是正確的),那么此單詞連續(xù)九次出現(xiàn)的時間以及兩次間時間間隔趨勢如下圖所示: (X軸為單詞出現(xiàn)是時間,Y軸為兩次出現(xiàn)時間的間隔)
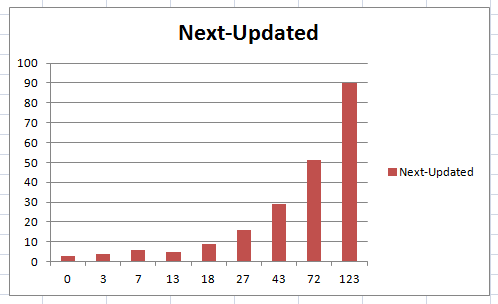
從圖表中可以看出,一個'熟悉'的單詞,出現(xiàn)的間隔會越來越長.這復合基本邏輯--熟悉的單詞不用經(jīng)常記憶.
2. 相反,假定某個單詞起始為'熟悉',但在其后選擇中,選擇'沒概念',且判定為'錯誤'(意思是自己確實對此單詞'沒概念',)(這里跟前面的解釋一起理解時,有點亂...),那么此單詞連續(xù)九次出現(xiàn)的 時間間隔趨勢如下:
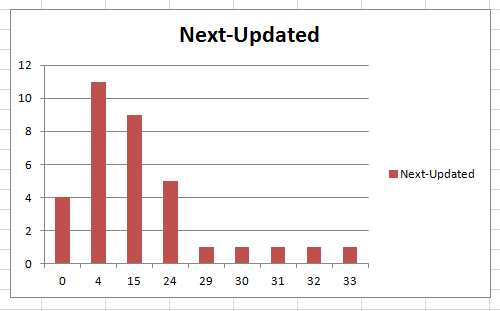
由上圖可見,隨著選擇'沒概念'的次數(shù)增加,單詞出現(xiàn)的間隔不斷變小,直至為1.
3. 下面趨勢圖顯示了當一個單詞每次都選擇'熟悉',但判定依次為'正確'和'錯誤',連續(xù)九次出現(xiàn)后的時間間隔變化:

4. 最后一個則是單詞每次選擇'沒概念'但判定依次為'正確'和'錯誤'的時間間隔趨勢圖:
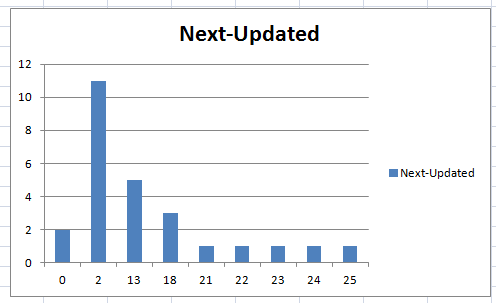
'熟悉度'一共有4級,且有兩個參數(shù),加上'判定'參數(shù)的2級,三個參數(shù)組合起來的系數(shù)關(guān)系就是前面的兩個數(shù)組,我是沒敢測試每種組合的趨勢,挑了上面四個最簡單的可能,其他的大家有興趣自己看吧...歡迎指點,歡迎拍磚,但不許打臉...
<---- 判定意思好混亂的分割線 ---->
剛才突然想起一個好方法,可以屏蔽'判定'概念,這就去改...