原文地址:
http://www.gamedev.net/reference/articles/article2003.asp
概述
雖然掌握了
A*
算法的人認(rèn)為它容易,但是對(duì)于初學(xué)者來說,
A*
算法還是很復(fù)雜的。
搜索區(qū)域(The Search Area)
我們假設(shè)某人要從
A
點(diǎn)移動(dòng)到
B
點(diǎn),但是這兩點(diǎn)之間被一堵墻隔開。如圖
1
,綠色是
A
,紅色是
B
,中間藍(lán)色是墻。
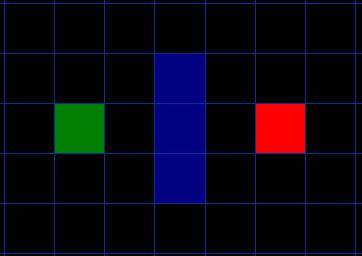
圖
1
你應(yīng)該注意到了,我們把要搜尋的區(qū)域劃分成了正方形的格子。這是尋路的第一步,簡(jiǎn)化搜索區(qū)域,就像我們這里做的一樣。這個(gè)特殊的方法把我們的搜索區(qū)域簡(jiǎn)化為了
2
維數(shù)組。數(shù)組的每一項(xiàng)代表一個(gè)格子,它的狀態(tài)就是可走
(walkalbe)
和不可走
(unwalkable)
。通過計(jì)算出從
A
到
B
需要走過哪些方格,就找到了路徑。一旦路徑找到了,人物便從一個(gè)方格的中心移動(dòng)到另一個(gè)方格的中心,直至到達(dá)目的地。
方格的中心點(diǎn)我們成為“節(jié)點(diǎn)
(nodes)
”。如果你讀過其他關(guān)于
A*
尋路算法的文章,你會(huì)發(fā)現(xiàn)人們常常都在討論節(jié)點(diǎn)。為什么不直接描述為方格呢?因?yàn)槲覀冇锌赡馨阉阉鲄^(qū)域劃為為其他多變形而不是正方形,例如可以是六邊形,矩形,甚至可以是任意多變形。而節(jié)點(diǎn)可以放在任意多邊形里面,可以放在多變形的中心,也可以放在多邊形的邊上。我們使用這個(gè)系統(tǒng),因?yàn)樗詈?jiǎn)單。
開始搜索(Starting the Search)
一旦我們把搜尋區(qū)域簡(jiǎn)化為一組可以量化的節(jié)點(diǎn)后,就像上面做的一樣,我們下一步要做的便是查找最短路徑。在
A*
中,我們從起點(diǎn)開始,檢查其相鄰的方格,然后向四周擴(kuò)展,直至找到目標(biāo)。
我們這樣開始我們的尋路旅途:
1.??????
從起點(diǎn)
A
開始,并把它就加入到一個(gè)由方格組成的
open list(
開放列表
)
中。這個(gè)
open list
有點(diǎn)像是一個(gè)購(gòu)物單。當(dāng)然現(xiàn)在
open list
里只有一項(xiàng),它就是起點(diǎn)
A
,后面會(huì)慢慢加入更多的項(xiàng)。
Open list
里的格子是路徑可能會(huì)是沿途經(jīng)過的,也有可能不經(jīng)過。基本上
open list
是一個(gè)待檢查的方格列表。
2.??????
查看與起點(diǎn)
A
相鄰的方格
(
忽略其中墻壁所占領(lǐng)的方格,河流所占領(lǐng)的方格及其他非法地形占領(lǐng)的方格
)
,把其中可走的
(walkable)
或可到達(dá)的
(reachable)
方格也加入到
open list
中。把起點(diǎn)
A
設(shè)置為這些方格的父親
(parent node
或
parent square)
。當(dāng)我們?cè)谧粉櫬窂綍r(shí),這些父節(jié)點(diǎn)的內(nèi)容是很重要的。稍后解釋。
3.??????
把
A
從
open list
中移除,加入到
close list(
封閉列表
)
中,
close list
中的每個(gè)方格都是現(xiàn)在不需要再關(guān)注的。
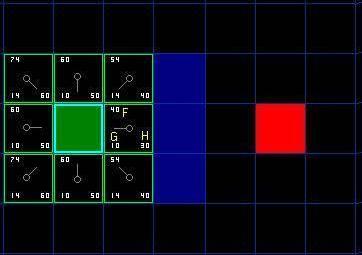
如下圖所示,深綠色的方格為起點(diǎn),它的外框是亮藍(lán)色,表示該方格被加入到了
close list
。與它相鄰的黑色方格是需要被檢查的,他們的外框是亮綠色。每個(gè)黑方格都有一個(gè)灰色的指針指向他們的父節(jié)點(diǎn),這里是起點(diǎn)
A
。

圖
2
。
下一步,我們需要從
open list
中選一個(gè)與起點(diǎn)
A
相鄰的方格,按下面描述的一樣或多或少的重復(fù)前面的步驟。但是到底選擇哪個(gè)方格好呢?具有最小
F
值的那個(gè)。
?
路徑排序(Path Sorting)
計(jì)算出組成路徑的方格的關(guān)鍵是下面這個(gè)等式:
F = G + H
這里,
G =
從起點(diǎn)
A
移動(dòng)到指定方格的移動(dòng)代價(jià),沿著到達(dá)該方格而生成的路徑。
H =
從指定的方格移動(dòng)到終點(diǎn)
B
的估算成本。這個(gè)通常被稱為試探法,有點(diǎn)讓人混淆。為什么這么叫呢,因?yàn)檫@是個(gè)猜測(cè)。直到我們找到了路徑我們才會(huì)知道真正的距離,因?yàn)橥局杏懈鞣N各樣的東西
(
比如墻壁,水等
)
。本教程將教你一種計(jì)算
H
的方法,你也可以在網(wǎng)上找到其他方法。
我們的路徑是這么產(chǎn)生的:反復(fù)遍歷
open list
,選擇
F
值最小的方格。這個(gè)過程稍后詳細(xì)描述。我們還是先看看怎么去計(jì)算上面的等式。
如上所述,
G
是從起點(diǎn)A移動(dòng)到指定方格的移動(dòng)代價(jià)。在本例中,橫向和縱向的移動(dòng)代價(jià)為
10
,對(duì)角線的移動(dòng)代價(jià)為
14
。之所以使用這些數(shù)據(jù),是因?yàn)閷?shí)際的對(duì)角移動(dòng)距離是
2
的平方根,或者是近似的
1.414
倍的橫向或縱向移動(dòng)代價(jià)。使用
10
和
14
就是為了簡(jiǎn)單起見。比例是對(duì)的,我們避免了開放和小數(shù)的計(jì)算。這并不是我們沒有這個(gè)能力或是不喜歡數(shù)學(xué)。使用這些數(shù)字也可以使計(jì)算機(jī)更快。稍后你便會(huì)發(fā)現(xiàn),如果不使用這些技巧,尋路算法將很慢。
?
既然我們是沿著到達(dá)指定方格的路徑來計(jì)算
G
值,那么計(jì)算出該方格的
G
值的方法就是找出其父親的
G
值,然后按父親是直線方向還是斜線方向加上
10
或
14
。隨著我們離開起點(diǎn)而得到更多的方格,這個(gè)方法會(huì)變得更加明朗。
?
有很多方法可以估算
H
值。這里我們使用
Manhattan
方法,計(jì)算從當(dāng)前方格橫向或縱向移動(dòng)到達(dá)目標(biāo)所經(jīng)過的方格數(shù),忽略對(duì)角移動(dòng),然后把總數(shù)乘以
10
。之所以叫做
Manhattan
方法,是因?yàn)檫@很像統(tǒng)計(jì)從一個(gè)地點(diǎn)到另一個(gè)地點(diǎn)所穿過的街區(qū)數(shù),而你不能斜向穿過街區(qū)。重要的是,計(jì)算
H
是,要忽略路徑中的障礙物。這是對(duì)剩余距離的估算值,而不是實(shí)際值,因此才稱為試探法。
?
把
G
和
H
相加便得到
F
。我們第一步的結(jié)果如下圖所示。每個(gè)方格都標(biāo)上了
F
,
G
,
H
的值,就像起點(diǎn)右邊的方格那樣,左上角是
F
,左下角是
G
,右下角是
H
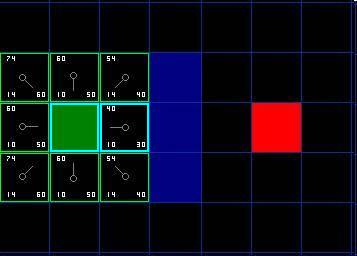
。
圖
3
好,現(xiàn)在讓我們看看其中的一些方格。在標(biāo)有字母的方格,
G = 10
。這是因?yàn)樗椒较驈钠瘘c(diǎn)到那里只有一個(gè)方格的距離。與起點(diǎn)直接相鄰的上方,下方,左方的方格的
G
值都是
10
,對(duì)角線的方格
G
值都是
14
。
?
H
值通過估算起點(diǎn)于終點(diǎn)
(
紅色方格
)
的
Manhattan
距離得到,僅作橫向和縱向移動(dòng),并且忽略沿途的墻壁。使用這種方式,起點(diǎn)右邊的方格到終點(diǎn)有
3
個(gè)方格的距離,因此
H = 30
。這個(gè)方格上方的方格到終點(diǎn)有
4
個(gè)方格的距離
(
注意只計(jì)算橫向和縱向距離
)
,因此
H = 40
。對(duì)于其他的方格,你可以用同樣的方法知道
H
值是如何得來的。
?
每個(gè)方格的
F
值,再說一次,直接把
G
值和
H
值相加就可以了。
?
繼續(xù)搜索(Continuing the Search)
為了繼續(xù)搜索,我們從
open list
中選擇
F
值最小的
(
方格
)
節(jié)點(diǎn),然后對(duì)所選擇的方格作如下操作:
4.??????
把它從
open list
里取出,放到
close list
中。
5.??????
檢查所有與它相鄰的方格,忽略其中在
close list
中或是不可走
(unwalkable)
的方格
(
比如墻,水,或是其他非法地形
)
,如果方格不在
open lsit
中,則把它們加入到
open list
中。
把我們選定的方格設(shè)置為這些新加入的方格的父親。
6.??????
如果某個(gè)相鄰的方格已經(jīng)在
open list
中,則檢查這條路徑是否更優(yōu),也就是說經(jīng)由當(dāng)前方格
(
我們選中的方格
)
到達(dá)那個(gè)方格是否具有更小的
G
值。如果沒有,不做任何操作。
相反,如果
G
值更小,則把那個(gè)方格的父親設(shè)為當(dāng)前方格
(
我們選中的方格
)
,然后重新計(jì)算那個(gè)方格的
F
值和
G
值。如果你還是很混淆,請(qǐng)參考下圖。
圖
4
Ok
,讓我們看看它是怎么工作的。在我們最初的
9
個(gè)方格中,還有
8
個(gè)在
open list
中,起點(diǎn)被放入了
close list
中。在這些方格中,起點(diǎn)右邊的格子的
F
值
40
最小,因此我們選擇這個(gè)方格作為下一個(gè)要處理的方格。它的外框用藍(lán)線打亮。
?
首先,我們把它從
open list
移到
close list
中
(
這就是為什么用藍(lán)線打亮的原因了
)
。然后我們檢查與它相鄰的方格。它右邊的方格是墻壁,我們忽略。它左邊的方格是起點(diǎn),在
close list
中,我們也忽略。其他
4
個(gè)相鄰的方格均在
open list
中,我們需要檢查經(jīng)由這個(gè)方格到達(dá)那里的路徑是否更好,使用
G
值來判定。讓我們看看上面的方格。它現(xiàn)在的
G
值為
14
。如果我們經(jīng)由當(dāng)前方格到達(dá)那里,
G
值將會(huì)為
20(
其中
10
為到達(dá)當(dāng)前方格的
G
值,此外還要加上從當(dāng)前方格縱向移動(dòng)到上面方格的
G
值
10)
。顯然
20
比
14
大,因此這不是最優(yōu)的路徑。如果你看圖你就會(huì)明白。直接從起點(diǎn)沿對(duì)角線移動(dòng)到那個(gè)方格比先橫向移動(dòng)再縱向移動(dòng)要好。
?
當(dāng)把
4
個(gè)已經(jīng)在
open list
中的相鄰方格都檢查后,沒有發(fā)現(xiàn)經(jīng)由當(dāng)前方格的更好路徑,因此我們不做任何改變。現(xiàn)在我們已經(jīng)檢查了當(dāng)前方格的所有相鄰的方格,并也對(duì)他們作了處理,是時(shí)候選擇下一個(gè)待處理的方格了。
?
因此再次遍歷我們的
open list
,現(xiàn)在它只有
7
個(gè)方格了,我們需要選擇
F
值最小的那個(gè)。有趣的是,這次有兩個(gè)方格的
F
值都
54
,選哪個(gè)呢?沒什么關(guān)系。從速度上考慮,選擇最后加入
open list
的方格更快。這導(dǎo)致了在尋路過程中,當(dāng)靠近目標(biāo)時(shí),優(yōu)先使用新找到的方格的偏好。但是這并不重要。
(
對(duì)相同數(shù)據(jù)的不同對(duì)待,導(dǎo)致兩中版本的
A*
找到等長(zhǎng)的不同路徑
)
。
?
我們選擇起點(diǎn)右下方的方格,如下圖所示。
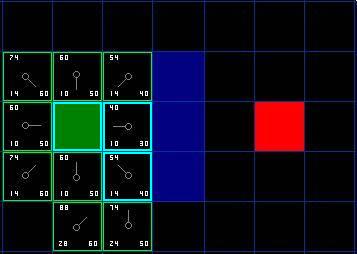
圖
5
?
這次,當(dāng)我們檢查相鄰的方格時(shí),我們發(fā)現(xiàn)它右邊的方格是墻,忽略之。上面的也一樣。
我們把墻下面的一格也忽略掉。為什么?因?yàn)槿绻淮┰綁堑脑挘悴荒苤苯訌漠?dāng)前方格移動(dòng)到那個(gè)方格。你需要先往下走,然后再移動(dòng)到那個(gè)方格,這樣來繞過墻角。
(
注意:穿越墻角的規(guī)則是可選的,依賴于你的節(jié)點(diǎn)是怎么放置的
)
?
這樣還剩下
5
個(gè)相鄰的方格。當(dāng)前方格下面的
2
個(gè)方格還沒有加入
open list
,所以把它們加入,同時(shí)把當(dāng)前方格設(shè)為他們的父親。在剩下的
3
個(gè)方格中,有
2
個(gè)已經(jīng)在
close list
中
(
一個(gè)是起點(diǎn),一個(gè)是當(dāng)前方格上面的方格,外框被加亮的
)
,我們忽略它們。最后一個(gè)方格,也就是當(dāng)前方格左邊的方格,我們檢查經(jīng)由當(dāng)前方格到達(dá)那里是否具有更小的
G
值。沒有。因此我們準(zhǔn)備從
open list
中選擇下一個(gè)待處理的方格。
?
不斷重復(fù)這個(gè)過程,直到把終點(diǎn)也加入到了
open list
中,此時(shí)如下圖所示。
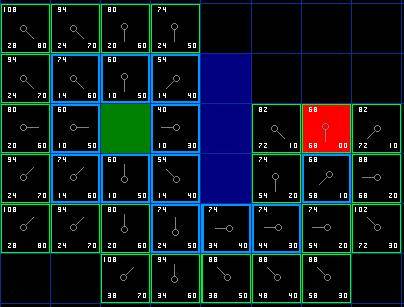
圖
6
?
注意,在起點(diǎn)下面
2
格的方格的父親已經(jīng)與前面不同了。之前它的
G
值是
28
并且指向它右上方的方格。現(xiàn)在它的
G
值為
20
,并且指向它正上方的方格。這在尋路過程中的某處發(fā)生,使用新路徑時(shí)
G
值經(jīng)過檢查并且變得更低,因此父節(jié)點(diǎn)被重新設(shè)置,
G
和
F
值被重新計(jì)算。盡管這一變化在本例中并不重要,但是在很多場(chǎng)合中,這種變化會(huì)導(dǎo)致尋路結(jié)果的巨大變化。
?
那么我們?cè)趺礃尤ゴ_定實(shí)際路徑呢?很簡(jiǎn)單,從終點(diǎn)開始,按著箭頭向父節(jié)點(diǎn)移動(dòng),這樣你就被帶回到了起點(diǎn),這就是你的路徑。如下圖所示。從起點(diǎn)
A
移動(dòng)到終點(diǎn)
B
就是簡(jiǎn)單從路徑上的一個(gè)方格的中心移動(dòng)到另一個(gè)方格的中心,直至目標(biāo)。就是這么簡(jiǎn)單!
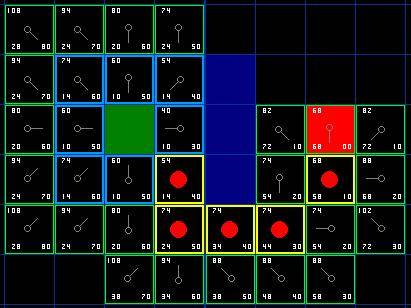
圖
7
?
A*算法總結(jié)(Summary of the A* Method)
Ok
,現(xiàn)在你已經(jīng)看完了整個(gè)的介紹,現(xiàn)在我們把所有步驟放在一起:
1.????????
把起點(diǎn)加入
open list
。
2.????????
重復(fù)如下過程:
a.????????
遍歷
open list
,查找
F
值最小的節(jié)點(diǎn),把它作為當(dāng)前要處理的節(jié)點(diǎn)。
b.????????
把這個(gè)節(jié)點(diǎn)移到
close list
。
c.????????
對(duì)當(dāng)前方格的
8
個(gè)相鄰方格的每一個(gè)方格?
◆????
如果它是不可抵達(dá)的或者它在
close list
中,忽略它。否則,做如下操作。
◆????
如果它不在
open list
中,把它加入
open list
,并且把當(dāng)前方格設(shè)置為它的父親,記錄該方格的
F
,
G
和
H
值。
◆????
如果它已經(jīng)在
open list
中,檢查這條路徑
(
即經(jīng)由當(dāng)前方格到達(dá)它那里
)
是否更好,用
G
值作參考。更小的
G
值表示這是更好的路徑。如果是這樣,把它的父親設(shè)置為當(dāng)前方格,并重新計(jì)算它的
G
和
F
值。如果你的
open list
是按
F
值排序的話,改變后你可能需要重新排序。
d.????????
停止,當(dāng)你
◆????
把終點(diǎn)加入到了
open list
中,此時(shí)路徑已經(jīng)找到了,或者
◆????
查找終點(diǎn)失敗,并且
open list
是空的,此時(shí)沒有路徑。
3.????????
保存路徑。從終點(diǎn)開始,每個(gè)方格沿著父節(jié)點(diǎn)移動(dòng)直至起點(diǎn),這就是你的路徑。
?
?
題外話(Small Rant)
請(qǐng)?jiān)徫业碾x題,當(dāng)你在網(wǎng)上或論壇上看到各種關(guān)于
A*
算法的討論時(shí),你偶爾會(huì)發(fā)現(xiàn)一些
A*
的代碼,實(shí)際上他們不是。要使用
A*
,你必須包含上面討論的所有元素
----
尤其是
open list
,
close list
和路徑代價(jià)
G
,
H
和
F
。也有很多其他的尋路算法,這些算法并不是
A*
算法,
A*
被認(rèn)為是最好的。在本文末尾引用的一些文章中
Bryan Stout
討論了他們的一部分,包括他們的優(yōu)缺點(diǎn)。在某些時(shí)候你可以二中擇一,但你必須明白自己在做什么。
Ok
,不廢話了。回到文章。
?
實(shí)現(xiàn)的注解(Notes on Implemetation)
現(xiàn)在你已經(jīng)明白了基本方法,這里是你在寫自己的程序是需要考慮的一些額外的東西。下面的材料引用了一些我用
C++
和
Basic
寫的程序,但是對(duì)其他語言同樣有效。
?
1.???
維護(hù)
Open List
:這是
A*
中最重要的部分。每次你訪問
Open list
,你都要找出具有最小
?? F
值的方格。有幾種做法可以做到這個(gè)。你可以隨意保存路徑元素,當(dāng)你需要找到具
???
有最小
F
值的方格時(shí),遍歷整個(gè)
open list
。這個(gè)很簡(jiǎn)單,但對(duì)于很長(zhǎng)的路徑會(huì)很慢。這個(gè)方法可以通過維護(hù)一個(gè)排好序的表來改進(jìn),每次當(dāng)你需要找到具有最小
F
值的方格時(shí),僅取出表的第一項(xiàng)即可。我寫程序時(shí),這是我用的第一個(gè)方法。
??????
??????
對(duì)于小地圖,這可以很好的工作,但這不是最快的方案。追求速度的
A*
程序員使用了叫做二叉堆的東西,我的程序里也用了這個(gè)。以我的經(jīng)驗(yàn),這種方法在多數(shù)場(chǎng)合下會(huì)快
2—3
倍,對(duì)于更長(zhǎng)的路徑速度成幾何級(jí)數(shù)增長(zhǎng)
(10
倍甚至更快
)
。如果你想更多的了解二叉堆,請(qǐng)閱讀
Using Binary Heaps in A* Pathfinding
。
2.??????
其他單位:如果你碰巧很仔細(xì)的看了我的程序,你會(huì)注意到我完全忽略了其他單位。我的尋路者實(shí)際上可以互相穿越。這取決于游戲,也許可以,也許不可以。如果你想考慮其他單位,并想使他們移動(dòng)時(shí)繞過彼此,我建議你的尋路程序忽略它們,再寫一些新的程序來判斷兩個(gè)單位是否會(huì)發(fā)生碰撞。如果發(fā)生碰撞,你可以產(chǎn)生一個(gè)新的路徑,或者是使用一些標(biāo)準(zhǔn)的運(yùn)動(dòng)法則(比如永遠(yuǎn)向右移動(dòng),等等)直至障礙物不在途中,然后產(chǎn)生一個(gè)新的路徑。為什么在計(jì)算初始路徑是不包括其他單位呢?因?yàn)槠渌麊挝皇强梢詣?dòng)的,當(dāng)你到達(dá)的時(shí)候它們可能不在自己的位置上。這可以產(chǎn)生一些怪異的結(jié)果,一個(gè)單位突然轉(zhuǎn)向來避免和一個(gè)已不存在的單位碰撞,在它的路徑計(jì)算出來后和穿越它路徑的那些單位碰撞了。
在尋路代碼中忽略其他單位,意味著你必須寫另一份代碼來處理碰撞。這是游戲的細(xì)節(jié),所以我把解決方案留給你。本文末尾引用的
Bryan Stout's
的文章中的幾種解決方案非常值得了解。
3.??????
一些速度方面的提示:如果你在開發(fā)自己的
A*
程序或者是改編我寫的程序,最后你會(huì)發(fā)現(xiàn)尋路占用了大量的
CPU
時(shí)間,尤其是當(dāng)你有相當(dāng)多的尋路者和一塊很大的地圖時(shí)。如果你閱讀過網(wǎng)上的資料,你會(huì)發(fā)現(xiàn)就算是開發(fā)星際爭(zhēng)霸,帝國(guó)時(shí)代的專家也是這樣。如果你發(fā)現(xiàn)事情由于尋路而變慢了,這里有些主意很不錯(cuò):
◆????
使用小地圖或者更少的尋路者。
◆????
千萬不要同時(shí)給多個(gè)尋路者尋路。取而代之的是把它們放入隊(duì)列中,分散到幾個(gè)游戲周期中。如果你的游戲以每秒
40
周期的速度運(yùn)行,沒人能察覺到。但是如果同時(shí)有大量的尋路者在尋路的話,他們會(huì)馬上就發(fā)現(xiàn)游戲慢下來了。
◆????
考慮在地圖中使用更大的方格。這減少了尋路時(shí)需要搜索的方格數(shù)量。如果你是有雄心的話,你可以設(shè)計(jì)多套尋路方案,根據(jù)路徑的長(zhǎng)度而使用在不同場(chǎng)合。這也是專業(yè)人士的做法,對(duì)長(zhǎng)路徑使用大方格,當(dāng)你接近目標(biāo)時(shí)使用小方格。如果你對(duì)這個(gè)有興趣,請(qǐng)看
Two-Tiered A* Pathfinding
。
◆????
對(duì)于很長(zhǎng)的路徑,考慮使用路徑點(diǎn)系統(tǒng),或者可以預(yù)先計(jì)算路徑并加入游戲中。
◆????
預(yù)先處理你的地圖,指出哪些區(qū)域是不可到達(dá)的。這些區(qū)域稱為“孤島”。實(shí)際上,他們可以是島嶼,或者是被墻壁等包圍而不可到達(dá)的任意區(qū)域。
A*
的下限是,你告訴他搜尋通往哪些區(qū)域的路徑時(shí),他會(huì)搜索整個(gè)地圖,直到所有可以抵達(dá)的方格都通過
open list
或
close list
得到了處理。這會(huì)浪費(fèi)大量的
CPU
時(shí)間。這可以通過預(yù)先設(shè)定不可到達(dá)的區(qū)域來解決。在某種數(shù)組中記錄這些信息,在尋路前檢查它。在我的
Blitz
版程序中,我寫了個(gè)地圖預(yù)處理程序來完成這個(gè)。它可以提前識(shí)別尋路算法會(huì)忽略的死路徑,這又進(jìn)一步提高了速度。
4.???
不同的地形損耗:在這個(gè)教程和我的程序中,地形只有
2
種:可抵達(dá)的和不可抵達(dá)
??????
的。但是如果你有些可抵達(dá)的地形,移動(dòng)代價(jià)會(huì)更高些,沼澤,山丘,地牢的樓梯
??????
等都是可抵達(dá)的地形,但是移動(dòng)代價(jià)比平地就要高。類似的,道路的移動(dòng)代價(jià)就比
??????
它周圍的地形低。
在你計(jì)算給定方格的
G
值時(shí)加上地形的代價(jià)就很容易解決了這個(gè)問題。簡(jiǎn)單的給這些方格加上一些額外的代價(jià)就可以了。
A*
算法用來查找代價(jià)最低的路徑,應(yīng)該很容易處理這些。在我的簡(jiǎn)單例子中,地形只有可達(dá)和不可達(dá)兩種,
A*
會(huì)搜尋最短和最直接的路徑。但是在有地形代價(jià)的環(huán)境中,代價(jià)最低的的路徑可能會(huì)很長(zhǎng)。
就像沿著公路繞過沼澤而不是直接穿越它。
另一個(gè)需要考慮的是專家所謂的“
influence Mapping
”,就像上面描述的可變成本地形一樣,你可以創(chuàng)建一個(gè)額外的計(jì)分系統(tǒng),把它應(yīng)用到尋路的
AI
中。假設(shè)你有這樣一張地圖,地圖上由個(gè)通道穿過山丘,有大批的尋路者要通過這個(gè)通道,電腦每次產(chǎn)生一個(gè)通過那個(gè)通道的路徑都會(huì)變得很擁擠。如果需要,你可以產(chǎn)生一個(gè)
influence map
,它懲罰那些會(huì)發(fā)生大屠殺的方格。這會(huì)讓電腦選擇更安全的路徑,也可以幫助它避免因?yàn)槁窂蕉蹋ó?dāng)然也更危險(xiǎn))而持續(xù)把隊(duì)伍或?qū)ぢ氛咚屯骋惶囟窂健?/span>
5.???
維護(hù)未探測(cè)的區(qū)域:你玩
PC
游戲的時(shí)候是否發(fā)現(xiàn)電腦總是能精確的選擇路徑,甚至地圖都未被探測(cè)。對(duì)于游戲來說,尋路過于精確反而不真實(shí)。幸運(yùn)的是,這個(gè)問題很容易修正。答案就是為每個(gè)玩家和電腦(每個(gè)玩家,不是每個(gè)單位
---
那會(huì)浪費(fèi)很多內(nèi)存)創(chuàng)建一個(gè)獨(dú)立的
knownWalkability
數(shù)組。每個(gè)數(shù)組包含了玩家已經(jīng)探測(cè)的區(qū)域的信息,和假設(shè)是可到達(dá)的其他區(qū)域,直到被證實(shí)。使用這種方法,單位會(huì)在路的死端徘徊,并會(huì)做出錯(cuò)誤的選擇,直到在它周圍找到了路徑。地圖一旦被探測(cè)了,尋路又向平常一樣工作。
6.???
平滑路徑:
A*
自動(dòng)給你花費(fèi)最小的,最短的路徑,但它不會(huì)自動(dòng)給你最平滑的路徑。看看我們的例子所找到的路徑(圖
7
)。在這條路徑上,第一步在起點(diǎn)的右下方,如果第一步在起點(diǎn)的正下方是不是路徑會(huì)更平滑呢?
??????
有幾個(gè)方法解決這個(gè)問題。在你計(jì)算路徑時(shí),你可以懲罰那些改變方向的方格,把它的
G
值增加一個(gè)額外的開銷。另一種選擇是,你可以遍歷你生成的路徑,查找那些用相鄰的方格替代會(huì)使路徑更平滑的地方。要了解更多,請(qǐng)看
Toward More Realistic Pathfinding
。
7.???
非方形搜索區(qū)域:在我們的例子中,我們使用都是
2D
的方形的區(qū)域。你可以使用不規(guī)則的區(qū)域。想想冒險(xiǎn)游戲中的那些國(guó)家,你可以設(shè)計(jì)一個(gè)像那樣的尋路關(guān)卡。你需要建立一張表格來保存國(guó)家相鄰關(guān)系,以及從一個(gè)國(guó)家移動(dòng)到另一個(gè)國(guó)家的
G
值。你還需要一個(gè)方法了估算
H
值。其他的都可以向上面的例子一樣處理。當(dāng)你向
open list
添加新項(xiàng)時(shí),不是使用相鄰的方格,而是查看表里相鄰的國(guó)家。
類似的,你可以為一張固定地形的地圖的路徑建立路徑點(diǎn)系統(tǒng)。路徑點(diǎn)通常是道路或地牢通道的轉(zhuǎn)折點(diǎn)。作為游戲設(shè)計(jì)者,你可以預(yù)先設(shè)定路徑點(diǎn)。如果兩個(gè)路徑點(diǎn)的連線沒有障礙物的話它們被視為相鄰的。在冒險(xiǎn)游戲的例子中,你可以保存這些相鄰信息在某種表中,當(dāng)
open list
增加新項(xiàng)時(shí)使用。然后記錄
G
值(可能用兩個(gè)結(jié)點(diǎn)間的直線距離)和
H
值(可能使用從節(jié)點(diǎn)到目標(biāo)的直線距離)。其它的都想往常一樣處理。
進(jìn)一步閱讀(Further Reading)
Ok
,現(xiàn)在你已經(jīng)對(duì)
A*
有了個(gè)基本的了解,同時(shí)也認(rèn)識(shí)了一些高級(jí)的主題。我強(qiáng)烈建議你看看我的代碼,壓縮包里包含了
2
個(gè)版本的實(shí)現(xiàn),一個(gè)是
C++
,另一個(gè)是
Blitz Basic
。
2
個(gè)版本都有注釋,你以該可以很容易就看懂。下面是鏈接:
Sample Code: A* Pathfinder (2D) Version 1.71
。
?
如果你不會(huì)使用
C++
或是
BlitzBasic
,在
C++
版本下你可以找到兩個(gè)
exe
文件。
BlitzBasic
版本必須去網(wǎng)站
Blitz Basic
下載
BlitzBasic 3D
的免費(fèi)
Demo
才能運(yùn)行。
在這里
here
你可以看到一個(gè)
Ben O'Neill
的
A*
在線驗(yàn)證實(shí)例。
?
你應(yīng)該閱讀下面這幾個(gè)站點(diǎn)的文章。在你讀完本教程后你可以更容易理解他們。
:
Amit Patel
的這篇文章被廣泛引用,但是如果你沒有閱讀本教程的話,你可能會(huì)感到很迷惑。尤其是你可以看到
Amit Patel
自己的一些想法。
Smart Moves: Intelligent Path Finding
:
Bryan Stout
的這篇需要去
Gamasutra.com
注冊(cè)才能閱讀。
Bryan
用
Delphi
寫的程序幫助我學(xué)習(xí)了
A*
,同時(shí)給了我一些我的程序中的一些靈感。他也闡述了
A*
的其他選擇。
Terrain Analysis
:
Dave Pottinger
一篇非常高階的,有吸引力的文章。他是
Ensemble Studios
的一名專家。這個(gè)家伙調(diào)整了游戲帝國(guó)時(shí)代和王者時(shí)代。不要期望能夠讀懂這里的每一樣?xùn)|西,但是這是一篇能給你一些不錯(cuò)的主意的很有吸引力的文章。它討論了包
mip-mapping
,
influence mapping
,和其他高階
AI
尋路主題。他的
flood filling
給了我在處理死路徑
”dead ends”
和孤島
”island”
時(shí)的靈感。這包含在我的
Blitz
版本的程序里。
?
下面的一些站點(diǎn)也值得去看看:
·????????????????????
aiGuru: Pathfinding
·????????????????????
Game AI Resource: Pathfinding
·????????????????????
GameDev.net: Pathfinding
謝謝。