重新看了KMP算法,有了新的理解。主要參考資料
/Files/bon/kmp2.pdf附件里說得很好,跟傳統(tǒng)的教程不同。
首先定義串s的前綴s',空串也是s的前綴,還有一個定義叫做proper prefix:s'是s的proper prefix等價于s'是s的prefix且s' != s,這個定義對于理解KMP有著關(guān)鍵的作用。同樣可以定義對應(yīng)的后綴以及proper suffix。
下面假設(shè)模式串為s,被匹配的串為t,且第0個字符是串的第一個字符。
KMP的精髓在于計算next數(shù)組(附件里為pi數(shù)組)。next[i]=k,k<i(注意這里不取等號,想想為什么),s[0...k]是s的proper prefix,也是s[0...i]的proper suffix,且k是最大的(即不存在l>k,s[0...l]是s[0...i]的proper prefix且是s[0...i]的proper suffix)。
那么next[0]=-1就很自然地被理解:表示的是空串是s[0...0]的proper prefix且是s[0...0]的proper suffix。
另外k嚴(yán)格小于i也可以理解:若k==i,但s[0...i]不是s[0...i]的proper prefix 也不是proper suffix,這跟定義沖突。
上述可以用下圖來說明。

上面的式子定義了next數(shù)組,但還沒有指出怎么計算next。假設(shè)next[0...i]已經(jīng)計算出來了,next[i+1]怎么算。
這里用的是動態(tài)規(guī)劃的思想。設(shè)s[0...k+1]是s[0...i+1]最長的proper prefix且是proper suffix,k<i,則明顯地s[0...k+1]符合以下性質(zhì):
1. s[0...k]是s[0...i]的proper prefix (這一點(diǎn)很明顯,由于k<i)
2. 且s[0...k]是s[0...i]的proper suffix (若不然,s[0...k+1]肯定無法組成s[0...i+1]的suffix)
3. 且s[k+1]==s[i+1]。
因此我們的任務(wù)就是找到這樣一個k。而s[0...k]是s[0...i]的proper prefix 和proper suffix這個性質(zhì)使得我們可以利用已計算的next[0...i]來找k。
找的過程實(shí)質(zhì)就是找到s[0...i+1]一個最長的proper prefix s[0...k], 這個prefix 同時是s[0...i+1]的proper suffix且有s[i+1]==s[k+1],見下圖:
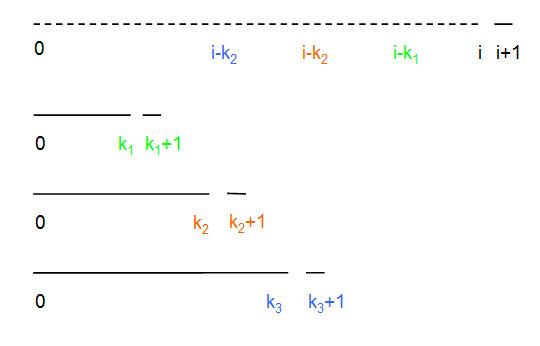
假設(shè)s[0...kx]都是s[0...i+1]的proper prefix,且都是s[0...i]的proper suffix。設(shè)s[k
1+1] != s[i+1],則s[0...k
1+1]不可能是s[0...i+1]的proper suffix。
設(shè)s[k
2+1] = = s[k
3+1] = = s[i+1],但由于k
3>k
2,所以next[i+1] = k
3+1
下面看poj上的一道
題目的代碼:
1 #include <iostream>
2
3 using namespace std;
4
5 char w[10001],t[1000001];
6 int n;
7 int next[10001];
8
9 int main()
10 {
11 scanf("%d",&n);
12 while(n--){
13 scanf("%s",w);
14 scanf("%s",t);
15 // process w
16 int wLength = strlen(w);
17 next[0]=-1;
18 int i=1;
19 int p;
20 while(i<wLength){
21 p=next[i-1];
22 while(p!=-1 && w[p+1]!=w[i]) p=next[p];
23 if(w[p+1]==w[i]) next[i]=p+1;
24 else next[i]=-1;
25 i++;
26 }
27 //for(i=0;i<wLength;i++) printf("%d",next[i]);
28 //printf("\n");
29 // matching
30 int j=-1,cnt=0;
31 i=-1;
32 int tLength = strlen(t);
33 while(j<tLength){
34 if(t[j+1]==w[i+1]){
35 i++;
36 j++;
37 if(i==wLength-1){
38 cnt++;
39 i=next[i];
40 }
41 }else{
42 if(i==-1) j++;
43 else i=next[i];
44 }
45 }
46 printf("%d\n",cnt);
47 }
48 return 1;
49 }
50