pku 3070題目要求計算Fibonacci數列的第n項最后4位。因為n可以很大(0 ≤
n ≤ 1,000,000,000)。因此直接計算在時限內是不可能的(有多個case)。題目還給出了計算的方法:表示成矩陣連乘的形式為
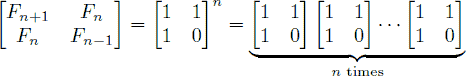
這就給我們提供了快速算法,因為矩陣相乘滿足結合律。預先計算上面一個矩陣的2的冪次方,再將n表示成2進制。如當n=5時,只需計算一次矩陣乘法:1次方乘以4次方。當n=1000000000時最多只需計算29次矩陣乘法2^29 = 536870912),而且由于矩陣只是2階,計算量大大減少。
// pku 3070 求fabonacci數列的快速算法
/*
化為以下矩陣連乘的形式
|F(n+1) F(n) | |1 1|(n)
|F(n) F(n-1)|=|1 0|
將n表示成2進制, 矩陣的二進制的積可以預先保存
只需計算結果的后4位
*/
#include <iostream>
using namespace std;
int m[31][4]; // 保存29個2階矩陣
long fact[31];// 2的k次方
void cal()
{
// 單位矩陣
//m[0][0]=1,m[0][1]=0,m[0][2]=0,m[0][3]=1;
m[1][0]=1,m[1][1]=1,m[1][2]=1,m[1][3]=0;
//fact[0]=1;
fact[1]=1;
for(int i=2;i<=30;i++)
{
m[i][0]=(m[i-1][0]*m[i-1][0]+m[i-1][1]*m[i-1][2])%10000;
m[i][1]=(m[i-1][0]*m[i-1][1]+m[i-1][1]*m[i-1][3])%10000;
m[i][2]=(m[i-1][2]*m[i-1][0]+m[i-1][3]*m[i-1][2])%10000;
m[i][3]=(m[i-1][2]*m[i-1][1]+m[i-1][3]*m[i-1][3])%10000;
fact[i]=2*fact[i-1];
}
}
void solve(long n)
{
// 對n表示成2進制
int e[31];
memset(e,0,sizeof(e));
int i,j;
for(i=30;i>=1;i--)
{
if(n>=fact[i])
{
e[i]=1;
n-=fact[i];
}
}
//for(i=1;i<=30;i++) printf("%d\n",e[i]);
// 結果矩陣,初始時為單位矩陣
int res[4]={1,0,0,1},tmp[4];
for(i=1;i<=30;i++)
{
if(e[i]!=0)
{
tmp[0]=(res[0]*m[i][0]+res[1]*m[i][2])%10000;
tmp[1]=(res[0]*m[i][1]+res[1]*m[i][3])%10000;
tmp[2]=(res[2]*m[i][0]+res[3]*m[i][2])%10000;
tmp[3]=(res[2]*m[i][1]+res[3]*m[i][3])%10000;
for(j=0;j<4;j++) res[j]=tmp[j];
}
}
printf("%d\n",res[1]);
}
int main()
{
cal();
long n;
while(scanf("%ld",&n) && n>=0)
{
solve(n);
}
return 1;
}