Cayley公式是說,一個完全圖K_n有n^(n-2)棵生成樹,換句話說n個節(jié)點(diǎn)的帶標(biāo)號的無根樹有n^(n-2)個。今天我學(xué)到了Cayley公式的一個非常簡單的證明,證明依賴于Prüfer編碼,它是對帶標(biāo)號無根樹的一種編碼方式。
給定一棵帶標(biāo)號的無根樹,找出編號最小的葉子節(jié)點(diǎn),寫下與它相鄰的節(jié)點(diǎn)的編號,然后刪掉這個葉子節(jié)點(diǎn)。反復(fù)執(zhí)行這個操作直到只剩兩個節(jié)點(diǎn)為止。由于節(jié)點(diǎn)數(shù)n>2的樹總存在葉子節(jié)點(diǎn),因此一棵n個節(jié)點(diǎn)的無根樹唯一地對應(yīng)了一個長度為n-2的數(shù)列,數(shù)列中的每個數(shù)都在1到n的范圍內(nèi)。下面我們只需要說明,任何一個長為n-2、取值范圍在1到n之間的數(shù)列都唯一地對應(yīng)了一棵n個節(jié)點(diǎn)的無根樹,這樣我們的帶標(biāo)號無根樹就和Prüfer編碼之間形成一一對應(yīng)的關(guān)系,Cayley公式便不證自明了。
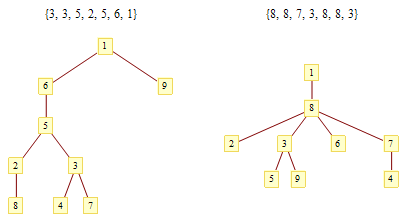
注意到,如果一個節(jié)點(diǎn)A不是葉子節(jié)點(diǎn),那么它至少有兩條邊;但在上述過程結(jié)束后,整個圖只剩下一條邊,因此節(jié)點(diǎn)A的至少一個相鄰節(jié)點(diǎn)被去掉過,節(jié)點(diǎn)A的編號將會在這棵樹對應(yīng)的Prüfer編碼中出現(xiàn)。反過來,在Prüfer編碼中出現(xiàn)過的數(shù)字顯然不可能是這棵樹(初始時)的葉子。于是我們看到,沒有在Prüfer編碼中出現(xiàn)過的數(shù)字恰好就是這棵樹(初始時)的葉子節(jié)點(diǎn)。找出沒有出現(xiàn)過的數(shù)字中最小的那一個(比如④),它就是與Prüfer編碼中第一個數(shù)所標(biāo)識的節(jié)點(diǎn)(比如③)相鄰的葉子。接下來,我們遞歸地考慮后面n-3位編碼(別忘了編碼總長是n-2):找出除④以外不在后n-3位編碼中的最小的數(shù)(左圖的例子中是⑦),將它連接到整個編碼的第2個數(shù)所對應(yīng)的節(jié)點(diǎn)上(例子中還是③)。再接下來,找出除④和⑦以外后n-4位編碼中最小的不被包含的數(shù),做同樣的處理……依次把③⑧②⑤⑥與編碼中第3、4、5、6、7位所表示的節(jié)點(diǎn)相連。最后,我們還有①和⑨沒處理過,直接把它們倆連接起來就行了。由于沒處理過的節(jié)點(diǎn)數(shù)總比剩下的編碼長度大2,因此我們總能找到一個最小的沒在剩余編碼中出現(xiàn)的數(shù),算法總能進(jìn)行下去。這樣,任何一個Prüfer編碼都唯一地對應(yīng)了一棵無根樹,有多少個n-2位的Prüfer編碼就有多少個帶標(biāo)號的無根樹。
一個有趣的推廣是,n個節(jié)點(diǎn)的度依次為D1, D2, ..., Dn的無根樹共有(n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]個,因?yàn)榇藭rPrüfer編碼中的數(shù)字i恰好出現(xiàn)Di-1次。