Posted on 2010-06-23 00:08
王之昊 閱讀(538)
評論(1) 編輯 收藏 引用 所屬分類:
三維幾何 、
分類討論 、
intricate

題意: 給一個正八面體,有只螞蟻要從面上一點走到另一點,只能沿表面走,求最短距離。
為了討論方便,首先給所有頂點標號,如圖所示.
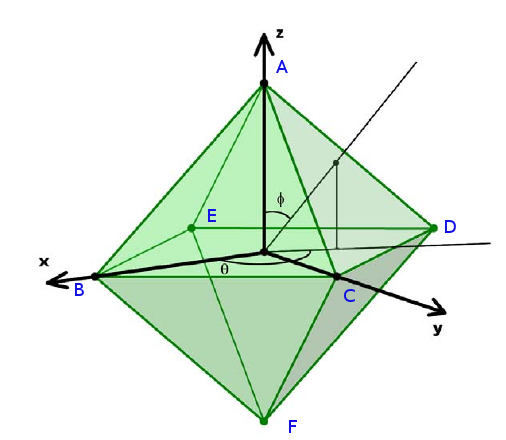
分四類討論:
1)共面情況( 兩點都在面ABC上 )
兩點之間直線最短, 這時直接計算兩點之間距離
2)相鄰面情況(一點在面ABC上, 一點在面ACD上 )
最短路徑只可能是兩個相鄰面攤開的直線距離,如圖所示:
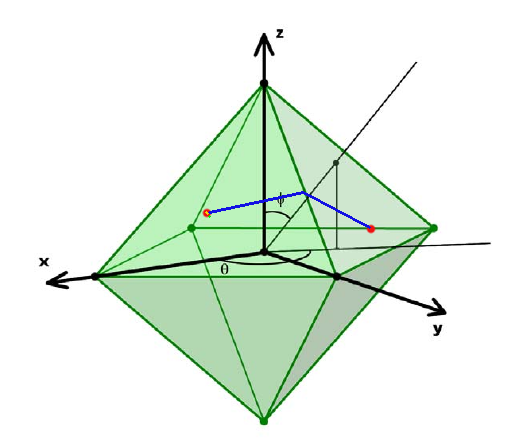
其他路徑可以反射到這兩個面上證明他們不是最優的.例如:
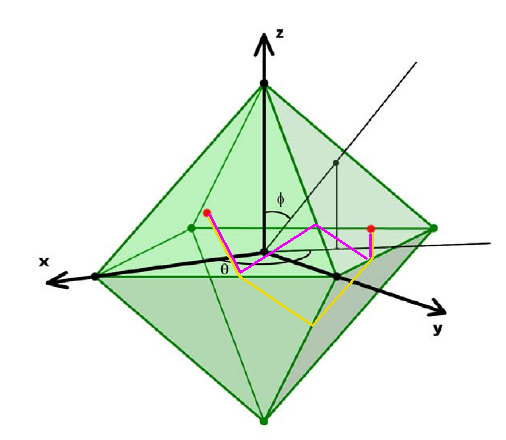
紅線路徑和黃線路徑是等價的,而紅線路徑顯然沒有前一幅圖的藍線路徑優.
3)同在上側的“對立面”情況( 一點在面ABC上, 一點在面ADE上 ).
最優情況有兩種:
- 從 面ABC 到 面ACD 到 面ADE
- 從 面ABC 到 面ABE 到 面ADE
同2)一樣利用反射的方法可以證明其他走法不是最優的.
4)嚴格“對面”情況(一點在面ABC上, 一點在面DEF上 )。
枚舉所有可能的六種情況.
其他的情況都可以通過坐標變換轉化成這四種情況