題意：有四個(gè)圓大小不一，可以隨意移動(dòng)他們，求包圍這四個(gè)圓的最小園？

首先應(yīng)該是二分答案，變成一個(gè)判定性問題。

對(duì)于某個(gè)固定半徑 R 的目標(biāo)圓，假設(shè)它的圓心 C0 在(0,0)。其他四個(gè)圓的圓心 Pi 只要滿足 | Pi - C0 | + ri <= R 即可。可以想象Pi 應(yīng)當(dāng)盡量的離 C0越遠(yuǎn)越好， 越遠(yuǎn)越有希望放下，當(dāng)然在滿足上面的條件下。

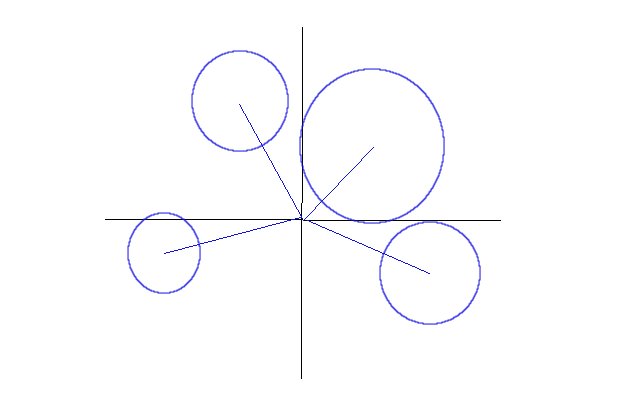
這樣四個(gè)圓的圓心離原點(diǎn)的距離就確定了，現(xiàn)在可以想像成有四個(gè)杠桿,每個(gè)杠桿的頭上有一個(gè)圓,杠桿可以繞著原點(diǎn)轉(zhuǎn)動(dòng),圓是剛性的,接著就判斷這種情況是否可能發(fā)生.

實(shí)際上只要讓他們一個(gè)挨著一個(gè)放就可以了.比如可以 放置第i個(gè)時(shí),盡量挨著逆時(shí)針方向的前i-1個(gè),并且判斷會(huì)不會(huì)沿順時(shí)針方向和前i-1個(gè)沖突.

這里還有些不太清楚的地方:比如順序是否有關(guān)?