有環鏈表面試題(轉帖)
鏈表在面試中出現的頻率很高,有的比較正常,考鏈表的常規操作,主要看基本功是否扎實,有些就比較難,難在思維的改變和是否能夠想到對應的點。這里
出現的是其中一個題目,我稱之為有環鏈表問題。也就是從判斷一個單鏈表是否存在循環而擴展衍生的問題。下面來看問題如何
解決。
首先來看最基本的這個問題:如何判斷一個單鏈表是否存在循環,鏈表數目未知。算法不能破壞鏈表。
這里我們可以想到有三種解決的方法。
第一種方法,將所有的遍歷過的節點用某個結構存儲起來,然后每遍歷一個節點,都在這個結構中查找是否遍歷過,如果找到有重復,則說明該鏈表存在循
環;如果直到遍歷結束,則說明鏈表不存在循環。
這個結構我們可以使用hash來做,hash中存儲的值為節點的內存地址,這樣查找的操作所需時間為O(1),遍歷操作需要O(n),hash表的
存儲空間需要額外的O(n)。所以整個算法的時間復雜度為O(n),空間復雜度為O(n)。
第二種方法,比較的特別,是使用反轉指針的方法,每過一個節點就把該節點的指針反向。
當有環的時候,最后指針會定位到鏈表的頭部,如果到最后,都沒有再到頭部,那說明鏈表不存在循環。
這個方法會破壞掉鏈表,所以如果要求是不能破壞鏈表的話,我們最后就還需要反轉一下,再將鏈表恢復。
這個方法使用的空間復雜度為O(1),其實是使用了3個指針,用于進行反轉。同時,時間復雜度為O(n)。
第三種方法,可能大家已經知道了,同時也是面試官大多想要得到的答案,就是快慢指針。
快指針pf(f就是fast的縮寫)每次移動2個節點,慢指針ps(s為slow的縮寫)每次移動1個節點,如果快指針能夠追上慢指針,那就說明其
中有一個環,否則不存在環。
這個方法的時間復雜度為O(n),空間復雜度為O(1),實際使用兩個指針。
【擴展】
對于這個問題,還有一些擴展性的問題。比如:如何找到環的開始節點也就是環首,如何得到環的長度,如何解開環等等,其中的關鍵就是如何找到其中對應
的規律。
當快慢指針都進入環之后,可以觀察到快指針每
次都接近慢指針一個節點位置。這樣,當兩個指針相遇的時候,其從慢指針進入環開始走過的路程肯定是小于環的長度x的。而假設鏈表的第一個節點到環的開始節點的長度為y。
畫圖可以得知:
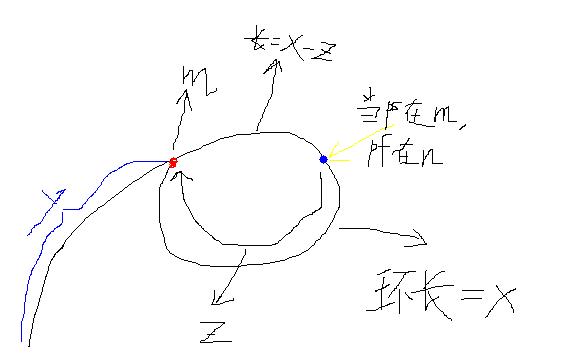
根據圖上面的示意,快指針pf需要追z個節點,就可以追上慢指
針ps,而一個iteration中pf會追上ps一個節點,所以需要用z個iteration。
當ps和pf相遇了,可以肯定的
是這兩個指針肯定是在環上相遇的。
此時,還是繼續一快一慢,根據上面得到的規律,經過環長x,這兩個指針第二次相
遇。這樣,我們可以得到環中一共有多少個節點。
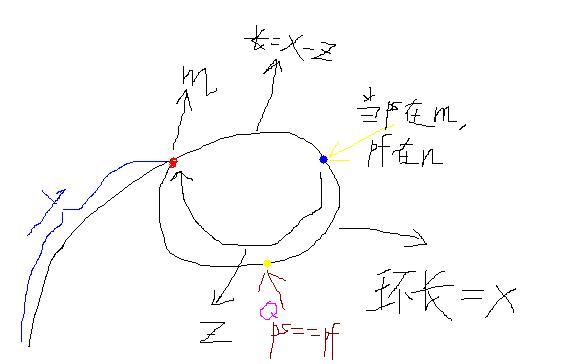
假設相遇點為Q點,Q點到m點的距離為r,第一次相遇的時候,ps走的距離為y+z,而pf走的距離為2y+2z,要求環的開
始節點位置,也就是求得y的值即可。
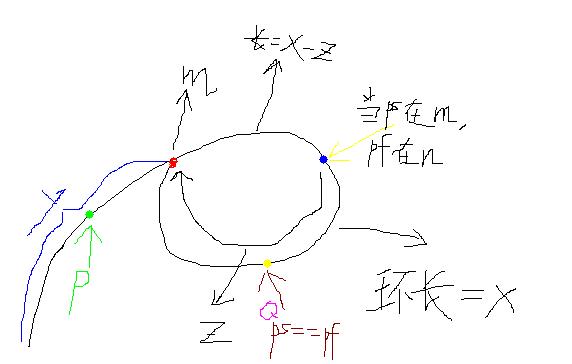
當重合的時候,pf走了2*all步,ps走了all步,此時兩個指針
都以步長為1進行回退,那ps就回退到第一個節點W,而pf回退到ps的位置。ps的位置就是Q點,此時從W點或Q點出發,x步之后,都會落到黃色的點Q點上。那因為此時使用的兩個指針都是步長為1的,那第一個重合的點是哪個呢?
可以看出是環首的紅色點m。而使用的步長就是y。
所以總結如下:
使用快慢指針,第一次相遇,表明存在循環。
繼續快慢指針,第二次相遇,得到的iteration步長
為環的長度。
分別從相遇點和第一個節點出發,都是步長為1的指針,當相遇時,得到的iteration步長為環首的位置。
這個題目的特殊情況就是指針
指向的就是第一個節點,那得到的就是一個循環鏈表。
附上擴展題的代碼

 Code
Code
1 bool hasLoop(linkedlist llist)
2 {
3 listnode *pf=llist;
4 listnode *ps=llist;
5
6 while(true)
7 {
8 if(pf && pf->next)
9 {
10 pf=pf->next->next;
11 }
12 else
13 return false;
14
15 ps=ps->next;
16
17 if(ps==pf)
18 {
19 //yes, there is a loop.
20 //if you just need to check if there is a loop, just return.
21 //but we need to extend it. So break to calc more.
22 break;
23 }
24 }
25
26 //calc the length of the circle.
27 int lengthX=0;
28 do{
29 ps=ps->next;
30 pf=pf->next->next;
31 lengthX++;
32 }while(ps!=pf)
33
34 //find the position of circle.
35 int lengthY=0;
36 linkedlistnode *p=llist;
37 while(p!=ps)
38 {
39 p=p->next;
40 ps=ps->next;
41 lengthY++;
42 }
43
44 printf("the length of circle is %d, the position of first elem in circle is %d.\n"lengthX, lengthY);
45
46 return true;
47 使用到的參考,多謝這些兄弟,不然還要多想好久:
1. http://www.cnblogs.com/shawn-zhou/archive/2008/11/26/1341307.html
2. http://bbs.chinaunix.net/viewthread.php?tid=896018
這段時間會開始陸續寫面試題的解決,希望大家多多提供題目,多多指教,多多討論,謝謝~
:)
PS:用chrome來發表文章很快,但是圖片和文章搭配的時候,似乎排版就有點小問題,不知道大家有沒有遇到過?
再PS:圖畫得不好,大家見諒哈