個人覺得這個博客把這個算法說的比較詳細了，直接搬過來吧，我再闡述一遍的話沒有人家說的好，還容易說錯。
==========================分割線之下摘自Sasuke_SCUT的blog==================================================
最小樹形圖，就是給有向帶權圖中指定一個特殊的點root，求一棵以root為根的有向生成樹T，并且T中所有邊的總權值最小。最小樹形圖的第一個算法是1965年朱永津和劉振宏提出的復雜度為O(VE)的算法。
判斷是否存在樹形圖的方法很簡單，只需要以v為根作一次圖的遍歷就可以了，所以下面的算法中不再考慮樹形圖不存在的情況。
在所有操作開始之前，我們需要把圖中所有的自環全都清除。很明顯，自環是不可能在任何一個樹形圖上的。只有進行了這步操作，總算法復雜度才真正能保證是O(VE)。
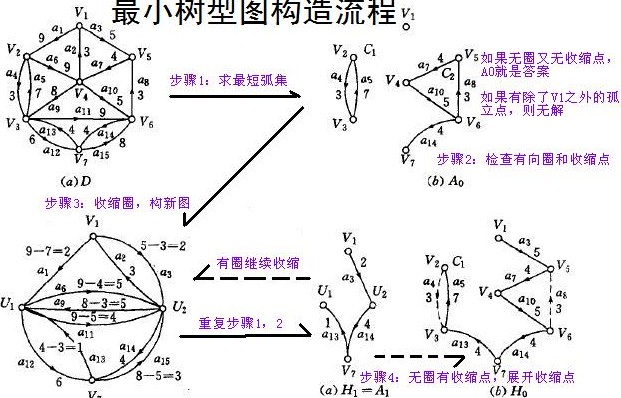
首先為除根之外的每個點選定一條入邊，這條入邊一定要是所有入邊中最小的。現在所有的最小入邊都選擇出來了，如果這個入邊集不存在有向環的話，我們可以證明這個集合就是該圖的最小樹形圖。這個證明并不是很難。如果存在有向環的話，我們就要將這個有向環所稱一個人工頂點，同時改變圖中邊的權。假設某點u在該環上，并設這個環中指向u的邊權是in[u]，那么對于每條從u出發的邊(u, i, w)，在新圖中連接(new, i, w)的邊，其中new為新加的人工頂點; 對于每條進入u的邊(i, u, w)，在新圖中建立邊(i, new, w-in[u])的邊。為什么入邊的權要減去in[u]，這個后面會解釋，在這里先給出算法的步驟。然后可以證明，新圖中最小樹形圖的權加上舊圖中被收縮的那個環的權和，就是原圖中最小樹形圖的權。
上面結論也不做證明了。現在依據上面的結論，說明一下為什么出邊的權不變，入邊的權要減去in [u]。對于新圖中的最小樹形圖T，設指向人工節點的邊為e。將人工節點展開以后，e指向了一個環。假設原先e是指向u的，這個時候我們將環上指向u的邊 in[u]刪除，這樣就得到了原圖中的一個樹形圖。我們會發現，如果新圖中e的權w'(e)是原圖中e的權w(e)減去in[u]權的話，那么在我們刪除掉in[u]，并且將e恢復為原圖狀態的時候，這個樹形圖的權仍然是新圖樹形圖的權加環的權，而這個權值正是最小樹形圖的權值。所以在展開節點之后，我們得到的仍然是最小樹形圖。逐步展開所有的人工節點，就會得到初始圖的最小樹形圖了。
如果實現得很聰明的話，可以達到找最小入邊O(E)，找環 O(V)，收縮O(E)，其中在找環O(V)這里需要一點技巧。這樣每次收縮的復雜度是O(E)，然后最多會收縮幾次呢？由于我們一開始已經拿掉了所有的自環，我門可以知道每個環至少包含2個點，收縮成1個點之后，總點數減少了至少1。當整個圖收縮到只有1個點的時候，最小樹形圖就不不用求了。所以我們最多只會進行V-1次的收縮，所以總得復雜度自然是O(VE)了。由此可見，如果一開始不除去自環的話，理論復雜度會和自環的數目有關。
========================分割線之上摘自Sasuke_SCUT的blog=====================================================

下面是朱劉算法的構造圖


下面是POJ 3164的代碼
POJ 3164