題目描述:
你是山西的一個煤老板,你在礦區開采了有3000噸煤需要運送到市場上去賣,從你的礦區
到市場有1000公里,你手里有一列燒煤的火車,這個火車最多只能裝1000噸煤,且其能耗比較大——每一公里需要耗一噸煤。請問,作為一個懂編程的煤老板的你,你會怎么運送
才能運最多的煤到集市?
下面我想闡述下我的思考過程:
確實是個好題,我開始沒想到好辦法,就開始試了幾組數據,大概的思路應該和大家的差不多: 就是設兩個中轉站,如下圖所示:
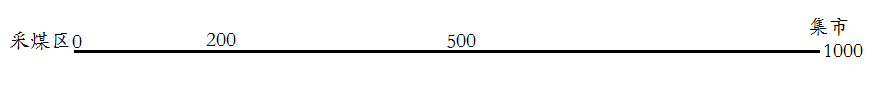
第一次嘗試:
具體的過程是這樣的:
第一趟: 從采煤區運1000噸煤到200公里處,這時消耗掉200噸,留下600噸,后攜帶200噸返回。
第二趟: 從采煤區運1000噸煤到200公里處,這時消耗200噸,但是我們增加200噸,這時200公里處剩下400噸,然后繼續前行到達500公里處,卸下400噸后返回,在200公里處在添加200噸煤,后返回到采煤區。
第三趟: 從采煤區1000噸煤到200公里處,增加200噸煤,然后繼續前行到500這個地方,這時我們的列車上還有700噸煤,我們添加300噸繼續前行到集市,我們這時還剩500噸。
所以運送到集市為500噸。
但是我們發現有100噸煤在500公里還沒用,說明還有改進空間。
第二次嘗試:
但是我發現200公里處是最優的,所以我假設我們需要兩個中轉站: x1公里處, x2公里處;同時我們令:x1 = 200;
我們按照上面的過程繼續 f1 表示x1的剩余量, f2表示 x2的剩余量;
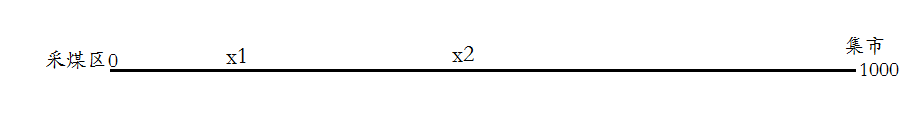
第一趟: f1 = 1000 - 2 * x1; f2 = 0;
第二趟: f1 = 1000 - 4 * x1; f2 = 1000 - 2* (x2-x1);
第三趟: f1 = 1000 - 5 * x1; f2 = 1000 - 2*(x2 – x1) + 1000 – (x2 – x1);
我們發現: 當我們把x1 = 200帶入得到: f1 = 0; f2 = 2600 – 3*x2;
我們假設我們取其中的f3 但是f3 <= 1000
最后的載運量令為f = f3 – (1000 – x2);
所以我們令f3 = 1000 得到f = 1600/3; 最優值大概是533.333…..
故事還沒結束:。。。。。
但是我們還沒發現完里面的玄機:我們發現 1600/3 – 200 = 1000/3;
這是偶然嗎,哦NO, 繼續 200 = 1000/5,
我們發現0-----x1 火車經過5次, x1 ----x2火車經過3次, 這是偶然嗎,當然不是
現在思考整個過程:1000噸在0 ---x1消耗的,需要5次, 同理1000噸是在x1----x2消耗,需要3次。
現在明白了吧其實結果就是1000/5 + 1000/3;
假設現在是4000噸煤呢: 道理很顯然了吧 1000/7 + 1000/5 + 1000/3
如果是一般情況呢: n*1000 (n>=2), 顯然n = 1 時答案為0
這個結果就是 1000 * (1/3 + 1/5 + 1/7 + ….. + 1 / (2*n-1)), 查了下這是個發散的級數,所以還是比較符合現實規律的, 煤假設是無窮的,那么運的也應該是無窮的。
不知道存在問題不, 希望大家給出
posted on 2011-04-12 23:10
Cunch 閱讀(3220)
評論(5) 編輯 收藏 引用 所屬分類:
YY