|
|
Problem Statement | | | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
We had a rectangular grid that consisted of W x H square cells. We placed a robot on one of the cells. The robot then followed the rules given below. - Initially, the robot is facing east.
- The robot moves in steps. In each step it moves to the adjacent cell in the direction it currently faces.
- The robot may not leave the grid.
- The robot may not visit the same cell twice. (This also means that it may not reenter the starting cell.)
- If a step forward does not cause the robot to break the above rules, the robot takes the step.
- Otherwise, the robot rotates 90 degrees to the left (counter-clockwise) and checks whether a step forward still breaks the above rules. If not, the robot takes the step and continues executing this program (still rotated in the new direction).
- If the rotation left did not help, the robot terminates the execution of this program.
- We can also terminate the execution of the program manually, at any moment.
For example, the following seven images show a series of moves made by the robot in a 12 x 11 board:
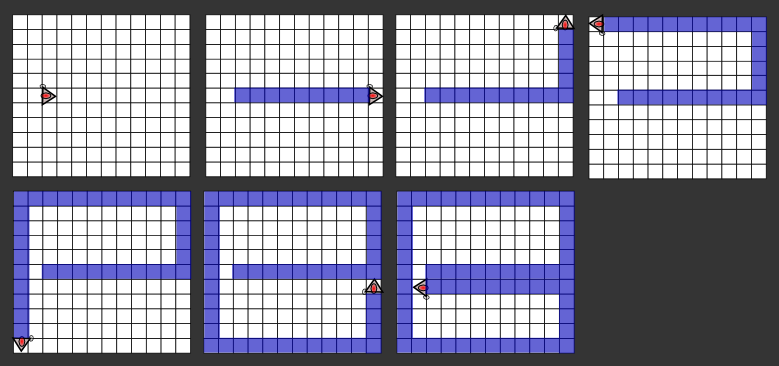
We forgot the dimensions of the grid and the original (x,y) coordinates of the cell on which the robot was originally placed, but we do remember its movement. You are given a vector <int> moves. This sequence of positive integers shall be interpreted as follows: The robot performed moves[0] steps eastwards, turned left, performed moves[1] steps northwards, turned left, and so on. After performing the last sequence of steps, the robot stopped. (Either it detected that it should terminate, or we stopped it manually.) We are not sure if the sequence of moves is valid. If the sequence of moves is impossible, return -1. Else, return the minimum area of a grid in which the sequence of moves is possible. (I.e., the return value is the smallest possible value of the product of W and H.). | Definition | | | | Class: | RotatingBot | | Method: | minArea | | Parameters: | vector <int> | | Returns: | int | | Method signature: | int minArea(vector <int> moves) | | (be sure your method is public) | | | |
| Constraints | | - | moves will contain between 1 and 50 elements, inclusive. | | - | Each element of moves will be between 1 and 50, inclusive. | Examples | | 0) |
| | | | | Returns: 16 | | The smallest valid board is a 16x1 board, with the robot starting on the west end of the board. | | | | 1) |
| | | | | Returns: 44 | | The smallest solution is to place the robot into the southwest corner of a 4 x 11 board. | | | | 2) |
| | | | | Returns: -1 | | This sequence of moves is not possible because the robot would return to its initial location which is forbidden. | | | | 3) |
| | | | | Returns: 132 | | These moves match the image from the problem statement. | | | | 4) |
| | | {12,1,27,14,27,12,26,11,25,10,24,9,23,8,22,7,21,6,20,5,19,4,18,3,17,2,16,1,15} | | Returns: 420 |
| | | 5) |
| | | | | 6) |
| | | | | 7) |
| | | | This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved. 模擬題目,直接按照給定序列遍歷,如果遇到不合法的情況return -1。設定四個方向,mw,me,mn,ms,東北西南,初始為上下界。然后依次找到范圍。 初始點(100,100)。 最后的面積為(me-mw+1)*(ms-mn+1) 沒有考慮完全啊,思維還是不嚴謹不完整,就WA了一組數據,昨晚做就悲劇了!!!! 我是弱菜,繼續努力! 不錯的模擬題目,需要考慮的東西很多! #include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>
#include <cassert>
#include <iostream>
#include <sstream>
#include <fstream>
#include <map>
#include <set>
#include <vector>
#include <queue>
#include <algorithm>
#define min(x,y) (x<y?x:y)
#define max(x,y) (x>y?x:y)
#define swap(t,x,y) (t=x,x=y,y=t)
#define clr(list) memset(list,0,sizeof(list))
using namespace std;
bool maps[205][205];
int go[4][2]={{1,0},{0,-1},{-1,0},{0,1}};
class RotatingBot{
public:
int minArea(vector <int> moves){
int n=moves.size();
int me=1000,mw=0,mn=0,ms=1000;
int tmp;
int dir;
int x,y,xx,yy;
clr(maps);
maps[100][100]=1;
x=100,y=100,dir=0;
for (int i=0;i<n ;i++)
{
tmp=moves[i];
for (int j=0;j<tmp;j++)
{
xx=x+go[dir][0];yy=y+go[dir][1];
if (maps[xx][yy] || (xx<mw || xx>me || yy<mn || yy>ms))
return -1;
else
{
maps[xx][yy]=1;
x=xx;y=yy;
}
}
xx=x+go[dir][0];yy=y+go[dir][1];
if (!maps[xx][yy])
{
if (dir==0)
if (me==1000)
me=x;
else
if (x<me && i<n-1)
return -1;
if (dir==1)
if (mn==0)
mn=y;
else if (y>mn && i<n-1)
return -1;
if (dir==2) //這里WA了testing 5 & 6
if (mw==0 && x<=100)
mw=x;
else
if (x>mw && i<n-1)
return -1;
if (dir==3) //最后栽在這里了
if (ms==1000 && y>=100)
ms=y;
else if ((y<ms || y<100) && i<n-1)
return -1;
}
dir=(dir+1) % 4;
}
// return mw;
if (mw==0)
mw=100;
if (mn==0)
mn=100;
if (ms==1000)
ms=100;
return (me-mw+1)*(ms-mn+1);
}
};

|