一道幾何題，解決方法很容易想到，不過要細心。

隨著輸入的順序，將矩形一個個放入集合，如果新的矩形與集合中的舊矩形相交，就將舊矩形分解，刪除舊矩形，放入新矩形和分解的矩形。

設矩形R1、R2，寬和高分別為(W1, H1)和(W2, H2)，兩矩形中心坐標分別為(X1, Y1)以及(X2, Y2)。判斷兩矩形是否相交（也就是是否有面積相重合），就看兩矩形中心坐標的豎直和水平距離是否小于兩矩形高的和的一半以及兩矩形寬的和的一半。即：

( |X1 - X2| < (W1 + W2) / 2 ) && ( |Y1 - Y2| < (H1 + H2) / 2 )

如果條件滿足，R1和R2即相交。

那相交會有幾種情況呢？我想到了16種：

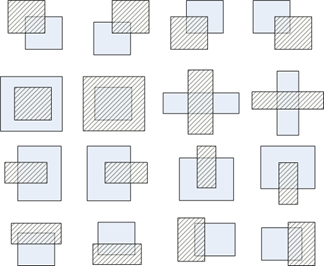
根據不同的情況，可以將原來的矩形分解為0～4個小矩形，這樣就可以解出來了。

（做幾何題可真費草稿紙啊，看來以后得學學matlab了，低碳、環保！）

另外，USACO還有一種解法，就是將矩形的四條邊進行離散化處理，將線段排序，然后再依次掃描，大體思路是這樣的，具體細節沒怎么看。