Permutation—全排列
l 簡介
一個全排列是從一個有限集中選取元素���,組成一個有序的序列�,并且所有的元素出現且僅出現一次����。
l 全排列的計數
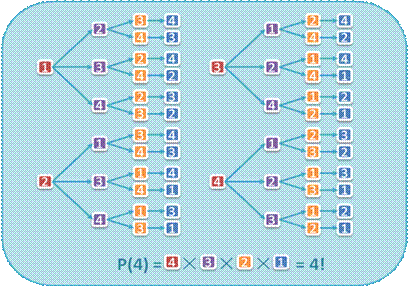
n 當集合中元素互異時,顯然全排列總共有n!個。
n 現在考慮集合中存在重復元素的情況:
1. 我們首先看一個簡單的例子�。
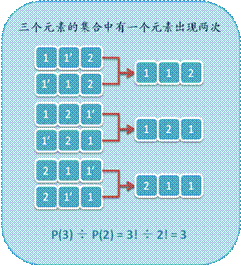
2. 設例子中的全排列數為P����,那么我們將這P個排列中重復的元素1看成互異的��,假設標記為1和1’,那么對于每種排列都能生成P(2) = 2!個惟一的新排列��,而這些新排列恰好構成了3個互異元素的全排列�,因此P = P(3) ÷P(2) = 3。
3. 假設n個元素的多重集合中有m個互異的元素�,各元素出現的次數分別為a1, a2, … , am��,且滿足(a1 + a2 + … + am) = n那么這個集合形成的全排列個數為
4. 當m = n時,上式的結果即為n!�。
l 生成全排列
n 遞推生成:每次輸出當前序列的下個全排列�,直到生成所有全排列����。
1. 按字典序生成:生成輸入序列按字典序的下個全排列。
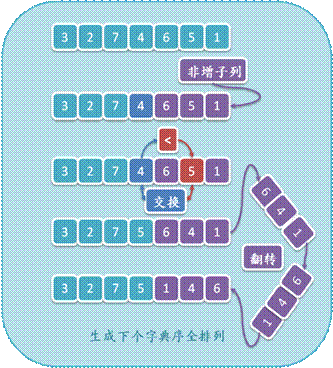
l 尋找從序列A末尾開始的最長非增連續子列S���。保存子列S之前的一個元素為a,在上圖中��,S = { 6, 5, 1 }�����,a = 4�����;
l 容易看出S是其元素的字典序最大全排列,如圖中的{ 6, 5, 1 }�����,因此無法通過在S內部交換元素得到A的下個字典序全排列�����,因此只需找出a + S,即序列{ 4, 6, 5, 1 }中的下個全排列。從序列末尾開始����,尋找第一個大于a的元素b���,如圖中的5����,交換a與b�。這樣我們更新了S之前的一個元素,只要將S變為其元素的字典序最小全排列即可得到A的下個字典序全排列���;
l 翻轉S,由于S為非增的(交換a與b后還是如此)����,那么翻轉后自然變成非減序列�,即其元素的字典序最小全排列�。
l 以上算法即C++中std::next_permutation函數的實現。
2. 無序生成:生成輸入序列的下個全排列�,各全排列間并不遵循特定的順序。
未完,待續……