原題叫“尋找發帖王”,其實就是在n個數里,存在一個數x,出現頻率超過n/2的數,要以最小的時間復雜度計算出這個x。
動機:
這個題目是昨晚無聊時,在CSDN論壇上看到的,起初我是這樣想的:既然有個數x出現頻率超過n/2,那如果排好序,那么第[n/2]個數一定就是x。這 樣問題就規約為這樣一個問題:“計算一組數的中位數”。《算法導論》有提出過解決辦法,就是類似快速排序那樣,使用分治算法,在O(n)復雜度內解決問 題。但算法性能依賴于數據的分布,最壞情況會達到O(n2)。
后來在網上搜了一下,發現這居然是《編程之美》上的。記得當初上大學的時候,我還看過,可怎么也想不起來了。看到書上提到的算法,不禁黯然稱奇!于是產生了個想法,我決定重新看一遍,并且寫一個系列的博客,寫下自己的心得。
引理:
n個數中,數x出現頻率超過n/2,那么從中去掉一對不相等的兩個數,x在剩下的(n-2)個數中的出現頻率依然超過n/2。
證明:
假設x出現了m次,則m > n/2,原頻率P0 = m/n > 1/2,從n個數中去掉一對不相同的兩個數<a, b>,有兩種情況:
- a != x, b != x。頻率P1 = m/(n-2) > m/n > 1/2
- a = x, b != x。 頻率P1 = (m - 1)/(n - 2)。P1 - P0 = (2m - n)/n(n - 2) > 0。則 P1 > P0 > 1/2
算法分析:
其實說到底非常簡單,就是在一堆數里隨便拿一個數,再找一個與它不相等的,然后一起扔掉,這樣問題規模不斷縮小,最終等到找不到一個不相等的數時,就成功 了。但要簡化算法,就不能每拿一個數就統統找一遍。可以考慮準備一個隊列,隊列里放著暫時扔不掉的數。如從頭開始,將a[0]放入隊列,再看a[1],如 果a[0] != a[1],則扔掉a[1]和a[0],a[0]從隊列取出;如果a[0] == a[1],則a[1]入隊列,然后a[2]進行相同的操作,以此類推。
解法依然可以優化。顯而易見,隊列里所有的數總是全部相等的,既然相等就沒有必要存入隊列,只要知道:1.假想的隊列里的數什么 2.隊列的長度。
這樣就得到了《編程之美》中的代碼了:
2 int candidate;
3 int count = 0;
4
5 for(size_t i = 0; i < size; i++) {
6 if (count == 0) {
7 candidate = arr[i];
8 count = 1;
9 }
10 else {
11 if (candidate == arr[i]) {
12 count++;
13 }
14 else {
15 count--;
16 }
17 }
18 }
19 return candidate;
20 }
應用:
代碼看似簡單,但我感到意猶未盡,正回味著,突然想到一個問題:如果條件(存在一個出現頻率超過一半的數)不滿足,那會出現什么情況?如何避免呢?
很顯然,我們的解法就是基于這樣一個條件的,一旦條件不滿足,得到的數就沒有任何意義。但不難發現,避免問題的出現也非常簡單:驗證找到的數是否出現頻率超過一半。
這也是個常用的方法:假設檢驗法。
對于一個數組,假設存在一個數,它出現頻率超過一半。然后在O(n)時間內找到這個數,再統計它出現的頻率。這樣就完美了!
于是可以得到一個同解的跳躍式問題:檢查一個數組中,是否存在一個數,它出現頻率超過一半。
]]>
真的非常想再現那串算法,于是自己開始推敲。我來談談我推敲的過程。
命題:給定整數x,y,計算較小值m。
兩個數的差異,在于他們的差,于是想到計算z = x - y,我想也許可以利用這個中間值,利用一些巧妙的位運算求出,可是貌似還是比較困難。于是我打算重新理一下思路:
可能出現的情況:(暫時忽略特殊情況 z = 0)
1. x < y
z < 0
就是要找到一個函數f,滿足f(y , z) = x
2. x > y
z > 0
就需要這個f不僅滿足1,而且滿足此時f(y , z) = y
因為算法的目的是使用加減法、位運算這些基本運算,盡可能簡單的計算。所以我選擇了加法運算
y + g(z) = x , z = x - y < 0;
y + g(z) = y , z = x - y > 0;
最終變成尋求一元函數g
就是
g(z) = z, z < 0
g(z) = 0, z > 0
也就是要找到一個一元分段函數,而且需要運算簡單,于是我想到了g(z) = (z >> 31) & z
如果z < 0,z>>31得到的是FFFFFFFF,再與上一個z,還是z,
如果z > 0, z>>31得到的是0000000,最終還是0
所以最終的算法是
z = x - y
m = ((z >> 31) & z) + y;
這個算法應該跟當初看到的比較接近了。它的優點很顯然,全部是最基本的運算,而且不包含控制指令,而且完全可以直接由寄存器計算完成,效率很高。
算法本身并非什么驚天地泣鬼神大算法,而且在編譯器里肯定會有自己做這樣的優化,其實最讓我欣慰的是我這次的思路,思路非常清晰,很久沒有動腦子的我,居然還能這么思考,我已經很高興了。其中主要包含兩種思想:分類討論、降低元數(降二元為一元)。這也是使用非常廣泛的方法了,前者主要幫助理清思路,后者主要降低復雜度。
Updated:
之前用的是z>>32,用gcc編譯會出現一個警告:
]]>
Aho-Corasick算法實踐
摘要:Aho-Corasick算法可以在文本串中識別一組關鍵字,所需時間和文本長度以及所有關鍵字的總長度成正比。該算法使用了一種稱為“trie”的特殊形式的狀態裝換圖。Trie是一個樹形結構的狀態裝換圖,從一個結點到它的各個子結點的邊上有不同的標號。Trie的葉子結點表示識別到的關鍵字。
在這里,將著重討論算法的實現。算法包含兩個部分,一是經典的KMP算法,二是KMP的擴展算法Aho-Corasick算法。前者實現單關鍵字的模式匹配,后者實現多關鍵字的匹配。(參考龍書詞法分析部分內容)
【源代碼:http://www.shnenglu.com/Files/yefeng/ACKMP.rar(vc9.0下測試通過) 】
一、經典KMP算法
當初,初學KMP算法時,總是通過反復的舉例去理解,沒有一種好的表達方式,而龍書描述這個算法使用了trie樹,也就是一個單鏈的狀態轉換圖。如模式b0b1...bn-1,trie樹如下: 
對模式串定義失效函數f:x->y,x,y in S,描述狀態轉移,f(s)表示在狀態s處,當下一個字符不是bs時轉向狀態f(s)繼續匹配。因此設置f(s)成為關鍵問題。
f(s)的存在其實主要是為了消除回溯。細節就不再多說了,這里只從原理上簡單說明。
設模式串為W,用文法描述,U、V表示W的一部分,w表示一個字符:
W -> UwV,
當U識別完成后,進入狀態s,識別w時,發現到來的字符不等于w,則需要轉向狀態f(s),f(s)到哪里去找呢?
那就要看U是什么樣子了。不管什么情況,只要U非空串,總可以表示成:
U -> uXu,或 U -> u,或U-> uXx,(x != u)
可以發現,前綴u是,如果后綴也是u,意味著主串中u已經被識別,如果還從模式串頭匹配u無疑是多余的,所以f(s)應該是識別前綴u后進入的狀態。然后再匹配下一個字符。而滿足條件的u可能會有多個,所以總是選擇最長的那個。偽代碼如下:
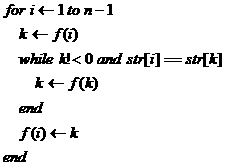
到此為止,應該算是可以結束KMP了,但實際情況下還可以對f函數進行優化。很多書本上描述的next數組就可以從f函數推導過來。
其實也顯然,設狀態s接收字符w,當與輸入字符c不等于c時,轉向狀態t,倘若t狀態也只接收字符w,顯然再次比較w與c是多余的,之后必然再次轉向狀態f(t)。在運行的時候,這些狀態轉換時沒有意義的,可以在構造f之后,直接將f(s)設置為f(t)提高運行效率(不過此時f函數的意義已經不同了)。f優化如下:
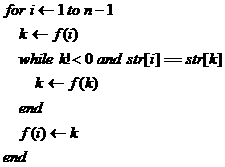
二、多關鍵字匹配與Aho-Corasick算法
Aho和Corasick對KMP算法進行了推廣,使它可以在一個文本串識別一個關鍵字集合中的任何關鍵字。在這種情況下,trie是一棵真正的樹,從其根結點開始就會出現分支。如果一個字符串是某個關鍵字的前綴,那么在trie中就又一個和該字符串對應的狀態。如關鍵字集合{he,she,his,hers},trie樹如下:
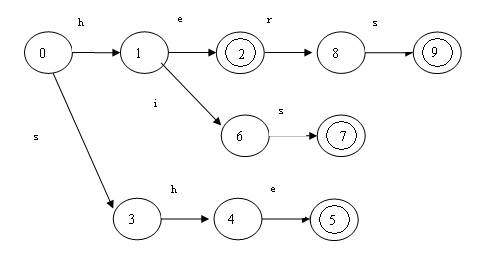
類似的,仍然構造類似KMP算法中那樣的實效函數。對于上面的例子,失效函數如下:
|
s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
f(s) |
-1 |
0 |
0 |
0 |
1 |
2 |
0 |
3 |
0 |
3 |
1.構造失效函數
類似KMP算法,同樣采用實效實效函數推進的方法,假設當前狀態為s,s的一個孩子結點的根結點根節點t狀態,如果當前的失效函數已知為f(s),則顯然地,f(t)必定是f(s)的孩子結點狀態,所要做的就是在狀態f(s)處尋找接受字符同s->t下一個狀態,如果能找到,那就是f(t),否則說明到s處匹配串的前綴長度太長,需縮減,所以需要找到更短的后綴,于是就到f(s)處繼續,如果仍然找不到,則轉到f(f(s))處,形成狀態的遞歸轉移。構造中需要遍歷之前結點的所有孩子,所以需采用廣度優先遍歷,偽代碼如下:
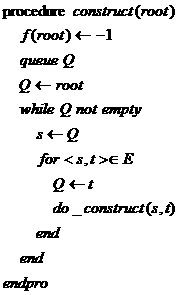
具體的構造如下:
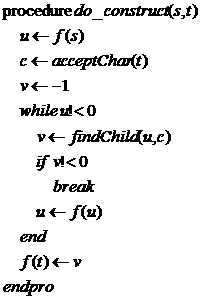
2.構造Trie樹
具體實現當然需要用到樹形結構了,顯然采用靜態鏈表應該是最適合的,因為樹構造完就不需要改變,而且當模式串比較多的時候可以減少內存碎片。
每一個結點有5個域:接受字符,下一個兄弟結點,第一個孩子結點,失效函數值,結點狀態。
但是有一種特殊情況,如上面的第二個圖,在進行匹配時,hers是永遠不會被匹配,因為he總是先于hers被匹配。這里就不考慮在內點狀態結束,這個問題暫時無法解決。于是可以做個特殊處理,只使用4個域,因為此時匹配成功后狀態就到了葉子結點,葉子結點不存在孩子域,這個域被浪費了,這里就可以借用一下,比如此域值為x,當x<0時,使用x xor 0x80000000表示識別到的模式串編號。
另一個棘手的問題是結點個數問題,這個數組到底多大?如何確定?
可以使用分值算法計算,先把模式串按字典順序排好序,設想n個排好序的模式串第i位排在一起,相同字符的組成一組,如AiBi…Xi,再把每組下一個字符,也就是第i+1位排在一起,相同字符的組成一組,如A’iB’I…X’i,以此遞歸運算。偽代碼如下:

3.缺點
水平有限,程序缺點很多,很多問題都沒有解決。
1.如果存在兩個模式串,一個是另一個的子串,那么后者將無法被匹配。
2.無法處理動態決定大小寫敏感性
3.不夠完整,只能向后匹配
]]>
看似很簡單的工作,設計中卻遇到了很多困難。
困難一:鍵盤按鍵分類
鍵盤按鍵有很多種分類方法。
第一種:按顯示分類。按住shift鍵,字母鍵、符號鍵顯示上面的字符;按下caps lock鍵,字母鍵切換為大寫字母。
第二種:按功能分類。大體有可顯示字符類、控制類。控制類包括shift,ctrl等。
為了解決可變的顯示問題,采用了一個自我感覺非常好的解決方案:字符集、鍵集相互獨立。如此一來,只要總體按照功能分類,通過特定功能的按鍵控制有效字符集即可,也就是說,對普通按鍵來說,它只負責到指定的字符集中去取對應序號的字符即可。
#pragma once
//字母標簽集合
class LabelSet
{
public:
LabelSet(LPCSTR* _pTable,int _n);
LPCSTR getLabel(int _id) const;
~LabelSet();
protected:
LabelSet(){}
private:
LPCSTR* pTable;
int n;
};
//相當于單刀雙擲開關組
class LabelSetEx
{
protected:
struct Switch
{
LabelSet* s[2];
int at;
};
public:
LabelSetEx(int _n);
bool addSets(int id,LPCSTR* s1,LPCSTR* s2,int n,int at = 0);
LPCSTR getLable(int id,int off) const;
void turn(int id);
~LabelSetEx();
private:
int n; //開關組總個數
Switch* pGroup; //開關組
};
//
//LabelSet.cpp
#include "StdAfx.h"
#include "LabelSet.h"
#include <algorithm>
#include <cassert>
using namespace std;
LabelSet::LabelSet( LPCSTR* _pTable,int _n )
{
n = _n;
pTable = new LPCSTR[n];
copy(_pTable,_pTable + _n,pTable);
}
LPCSTR LabelSet::getLabel( int _id ) const
{
return pTable[_id];
}
LabelSet::~LabelSet()
{
delete [] pTable;
}
LabelSetEx::LabelSetEx( int _n )
{
n = _n;
pGroup = new Switch[n];
memset(pGroup,0,n * sizeof(pGroup[0]));
}
LabelSetEx::~LabelSetEx()
{
while(n--)
{
if(pGroup[n].s[0] == pGroup[n].s[1])
delete pGroup[n].s[0];
else
{
delete pGroup[n].s[0];
delete pGroup[n].s[1];
}
}
delete [] pGroup;
}
bool LabelSetEx::addSets( int id,LPCSTR* s1,LPCSTR* s2,int n,int at /*= 0*/ )
{
assert((at & ~1) == 0);
if(pGroup[id].s[0] != NULL)
return false;
LabelSet* p = new LabelSet(s1,n);
pGroup[id].s[0] = p;
if(s1 == s2)
pGroup[id].s[1] = p;
else
pGroup[id].s[1] = new LabelSet(s2,n);
pGroup[id].at = at;
return true;
}
LPCSTR LabelSetEx::getLable( int id,int off ) const
{
Switch* p = pGroup + id;
return p->s[p->at]->getLabel(off);
}
void LabelSetEx::turn( int id )
{
assert((pGroup->at & ~1) == 0);
pGroup[id].at ^= 1;
}
//分類id的定義
#define LABEL_SET_ALPHA 0
#define LABEL_SET_SYMBOL 1
#define LABEL_SET_NUMPAD 2
#define LABEL_SET_MAIN 3
#define LABEL_SET_HELP 4
//字母串表
extern LPCSTR AlphaTable1[]; //小寫
extern LPCSTR AlphaTable2[]; //大寫
extern const int AlphaTableSize;
//符號串表
extern LPCSTR SymbolTable1[]; //下
extern LPCSTR SymbolTable2[]; //上
extern const int SymbolTableSize;
//小鍵盤數字表
extern LPCSTR NumPadTable1[]; //數字
extern LPCSTR NumPadTable2[]; //光標控制
extern const int NumPadTableSize;
//主鍵盤單顯
extern LPCSTR MainTable[];
extern const int MainTableSize;
//輔助鍵盤單顯
extern LPCSTR HelpTable[];
extern const int HelpTableSize;
struct KeyConfig
{
short id; //分類id
short offset; //類內偏移
RECT rt; //位置
BYTE vk; //虛擬碼
};
extern KeyConfig kcs[];
extern const int kcSize;
extern const SIZE kbSize;
言歸正傳,這樣的設計分離了按鍵與顯示,可配置能力大大加強。但仍然存在第二個大問題。
問題二:輸入焦點的確定
方案一:現在只要在網上搜索“虛擬鍵盤”,能夠搜到一大溜的源代碼,但只可惜全是同一份拷貝,而且存在一點小錯誤。他的解決方案是:利用 PreTranslateMessage,在底層調用它之前,前臺窗口仍然沒有改變,此時是獲得前一個前臺窗口的好時機,獲得后保存,并將使用 AttachThreadInput將當前線程綁定活動窗口的消息隊列,然后在單擊虛擬鍵盤時使用SetFocus將保存的窗口設為焦點(源代碼中同時使用了SetForgroundWindow和SetFocus,這是失效的原因),然后發送虛擬按鍵。
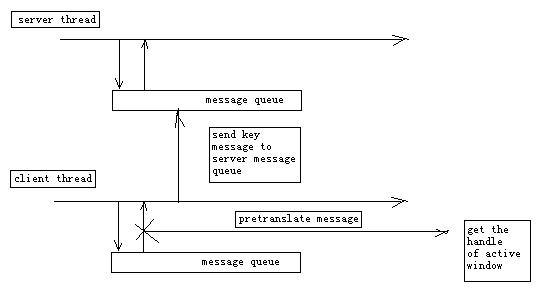
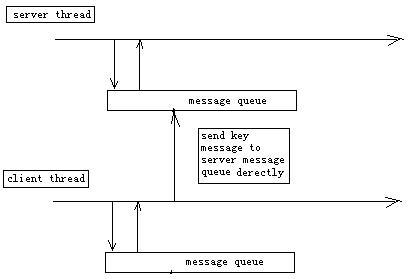
方案二:其實有更簡便的方法。設置主窗口屬性為WM_ES_NOACTIVATE,這樣窗口就不會成為前臺窗口,不管如何發送鍵盤消息,擁有焦點的窗口總會收到。但此時仍然存在問題。當移動窗口時,效果不大順暢,而且沒辦法響應菜單命令,那是因為該窗口始終不是前臺窗口造成的。解決方法就是在單擊標題欄時,成為前臺窗口,釋放是歸還前臺。
{
if(m_hForground == NULL)
{
m_hForground = ::GetForegroundWindow();
ModifyStyleEx(WS_EX_NOACTIVATE,0);
SetForegroundWindow();
}
CFrameWnd::OnNcLButtonDown(nHitTest, point);
}
{
if(m_hForground != NULL)
{
::SetForegroundWindow(m_hForground);
ModifyStyleEx(0,WS_EX_NOACTIVATE);
m_hForground = NULL;
}
CFrameWnd::OnNcMouseMove(nHitTest, point);
}
原本以為一般的按鍵就兩種狀態,通過down、up改變,如果用方波描述,down就是下降沿觸發,up是上升沿觸發。也曾了解,像shift這樣的按鍵會很復雜,存在多個狀態。后來測試發現,shift并非一個特例,所有的按鍵都有4個狀態,通過down、up改變狀態。只是不同按鍵對狀態的關注點不同。
可以做這樣一個測試,用GetKeyboardState得到各個虛擬碼對應的按鍵狀態。最高位為1時表示鍵被按下,最高位為1時,如果是lock鍵則表示被鎖住,對于其他鍵,各有各的作用。
比如一個鍵,用2位的二進制數表示這些狀態,設初始狀態為10,經過down后,變為01,經過up后,變為11,再經過down后,變為00,再經過up后,變為10,如此四個狀態經過down、up實現了周期性的狀態裝換。大體符合這樣的規律:
10-(down xor 11)->01->(up xor 10)->11-(down xor 11)->00(up xor 10)->10。
這樣,如果虛擬得比較徹底,在虛擬鍵盤內部可以輕易地實現狀態的記憶,并且可以獲得足夠的信息。對于顯示、控制都非常方便。
這只是第一個版本,還有很多問題需要解決。
待解決問題一:xml配置動態配置鍵盤,及動態更換顯示效果。
待解決問題二:同步物理鍵盤。
待解決問題三:更深層次,防止鍵盤消息被hook,初步認識,似乎可以使用剪貼板。
【源代碼1.2版本:http://www.shnenglu.com/Files/yefeng/VirtualKeyboard1.2.rar】
]]>