by Xguru
又說階乘，這是老生常談了吧。想都不用想，一個(gè)遞歸輕松搞定！
int factorial(int n)
{
if( n == 1)
return 1;
return n * factorial(n-1);
}或者你覺得遞歸效率沒有尾遞歸來的好 ，大筆一揮。
long fact_iter(long product, long counter, long maxcount)
{
return (counter > maxcount) ? product : fact_iter(product*counter, counter+1, maxcount);
}
long factorial(long n)
{
return fact_iter(1, 1, n);
}
或者你看過《代碼大全》上面說過：“如果為我工作的程序員用遞歸去計(jì)算階乘，那么我寧愿換人。”
使用遞歸求階乘速度緩慢，無(wú)法預(yù)測(cè)運(yùn)行期間內(nèi)存使用情況，難以理解。于是你把遞歸改成了循環(huán)語(yǔ)句。
int factorial(int n)
{
int result = 1;
for(int i = 2 ; i <= n; i++)
{
result = result * i;
}
return result;
}
當(dāng)你寫下這些代碼的時(shí)候，會(huì)不會(huì)覺得少了些什么？
在我的32位環(huán)境上測(cè)試一下，計(jì)算到33!的時(shí)候的溢出了，于是你會(huì)說，這是int的值太小了嘛，于是你換了個(gè)long double，測(cè)試一下，什么玩意嘛這是，數(shù)再大一點(diǎn)的話也不行了。
那就改用鏈表或者數(shù)組表示吧，鏈表的速度就太慢了，用數(shù)組吧。
int factorial2(int n,int a[])
{
int carry;
int digit = 1;
a[0] = 1;
int temp;
for(int i = 2; i <= n; ++i)
{
for(int j = 1, carry = 0; j <= digit; ++j)
{
temp = a[j-1] * i + carry;
a[j-1] = temp % 10;
carry = temp / 10;
}
while(carry)
{
a[++digit-1] = carry % 10;
carry /= 10;
}
}
return --digit;
}
這個(gè)算法模擬手工計(jì)算的過程，將結(jié)果保存在a數(shù)組中，返回的是結(jié)果的位數(shù)
你在這個(gè)時(shí)候是不是感覺輕飄飄了呢？請(qǐng)暫時(shí)打住。
如果我要求一個(gè)10W以上大數(shù)的一個(gè)科學(xué)計(jì)數(shù)法的表達(dá)式呢？或者是問你，求10W 級(jí)別上的N！左邊第三位的數(shù)字是多少？呃，這個(gè)是數(shù)學(xué)家的事了吧？振作精神，來挑戰(zhàn)自我吧！真正的程序員需要的就是這種追根究底的精神。
來試試數(shù)學(xué)分析方法，James Stirling這位蘇格蘭數(shù)學(xué)家，280多年前就給出了這個(gè)極限式子
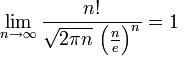
這個(gè)式子能用極快的速度求出n!的近似值，也可以使用它來無(wú)限接近準(zhǔn)確結(jié)果。具體的介紹和證明過程在這里 或者 這里。
斯特靈級(jí)數(shù)公式
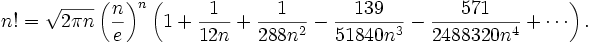
下面的代碼是求大數(shù)N！科學(xué)計(jì)數(shù)法表示
struct bigNum
{
double n; //尾數(shù)
int e; //指數(shù)
};
void factorial3(struct bigNum *p,int n)
{
double logx,s,item;//s:級(jí)數(shù)的和 item:級(jí)數(shù)的每一項(xiàng)
int i;
logx = n* log10((double)n/E);
p->e = (int)(logx); p->n= pow(10.0, logx-p->e);
p->n *= sqrt( 2* PI* (double)n);
for (item=1.0,s=0.0,i=0;i<sizeof(a1)/sizeof(double);i++)
{
s += item * a1[i];
item /= (double)n;
}
p->n *=s;
}
下面這個(gè)是階乘的對(duì)數(shù)的漸近展開式
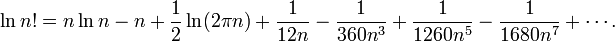
void factorial3b(struct bigNum *p,int n)
{
double logR;
double s,item;
int i;
logR=0.5*log(2.0*PI)+((double)n+0.5)*log(n)-(double)n;
for (item=1/(double)n,s=0.0,i=0;i<sizeof(a2)/sizeof(double);i++)
{
s+= item * a2[i];
item /= (double)(n)* (double)n;
}
logR+=s;
p->e = (int)( logR / log(10));//換底公式
p->n = pow(10.00, logR/log(10) - p->e);
}
要是求階層的位數(shù)也是特別簡(jiǎn)單
double getFactorialLength(int n)
{
return (n * log(double(n)) - n + 0.5 * log(2.0 * n * PI )) / log(10.0)+1;
}
這個(gè)求出來的是位數(shù)的近似數(shù)，或者是改進(jìn)一下，使用ceil函數(shù)來求出不小于給定實(shí)數(shù)的最小整數(shù)。
int getFactorialLength(int n)
{
if( n == 1 )
return 1;
else
return (int)ceil((N*log(N)-N+log(2*N*PI)/2)/log(10));
}
到此，你會(huì)不由感嘆：計(jì)算機(jī)科學(xué)中最閃光，最精髓，最本質(zhì)的東西還是數(shù)學(xué)！
芒德布羅集合的邊界
最后用羅素的話結(jié)束這篇隨筆：
Mathematics, rightly viewed, possesses not only truth, but supreme beauty — a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.
參考資料
1.Tom M. Apostol.《數(shù)學(xué)分析, 微積分》(Mathematical Analysis)
2.Steve McConnell.《代碼大全（第二版）》(CODE COMPLETE, Second Edition)
3.http://en.wikipedia.org/wiki/Stirling_approximation#History
4.http://mathworld.wolfram.com/StirlingsApproximation.html
5.http://zh.straightworldbank.com/wiki/%E6%96%AF%E7%89%B9%E6%9E%97%E5%85%AC%E5%BC%8F