糯米

這題做得人特別少，但實際上就是很普通的動態規劃。

思路：
由于飛到某個點的時候，后面的行程跟前面的行程沒有什么聯系，所以開一個二維數組 f[K][N]，
f[i][j] = { 從第 j 個點，第 i 個時刻開始飛行直到終點，所需要的最小花費 }

然后就從后往前推就可以了。

     摘要: 思路：這題就是平常玩的那種推箱子的游戲。不過簡化了一下，只是推一個箱子而已。用 bfs 來做，搜索樹里面的節點，也就是狀態，可以定義為：1. 箱子的坐標2. 上一次推完之后，人要走多少步才能到達箱子的上、下、左、右側。如果到達不了，值則為無窮大。這樣，狀態轉移的時候。就首先看是否能向某個方向推。如果能的話，就推一下。然后對人進行一次 bfs ，看下此時到達箱子的各個側要走多少步。就可以生成一個新的...  閱讀全文

思路：

一開始想到用線段樹來做，但是發現坐標范圍異常的大，放一個都勉勉強強，更不用說幾個了！
想了一下，發現有一個至關重要的條件“不存在覆蓋的情況”。
那就沒必要用線段樹了，因為壓根就沒必要解決覆蓋問題。
可以用一種取巧的方法解決這題。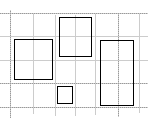



對于每個矩形，首先把它 y 方向的兩條邊抽取出來。
對于所有矩形的 y 方向的邊，先按照 x 排序，然后按照頂端的 y 坐標排序。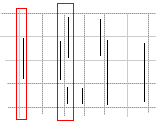



然后對于位于同一 x 坐標的邊，找出所有首尾相接或者有交集的邊。
那么這些邊對應的矩形必定要排除。

對于 x 方向的邊，作同樣的處理。

排除完之后，剩下的矩形就是可以答案了。

代碼 500 多ms。。

     摘要: 此題只有130人solved！也算小牛題了，剛開始看到的時候，打算不做了的，但后來想了一下，發現有一點點思路。經過好幾個小時的奮戰，居然做出來了！那感覺非常爽！思路：首先此題的變態之處是，要求比較的是排名，就不是單純的字符串匹配了。如果每次都重新求排名然后跟pattern比較，復雜度 O(NK)，八成會超時。關鍵是：一，不能每次都重新求排名二，不能逐個逐個的和pattern做比較看來也只有動態規...  閱讀全文

思路：
看到這題，第一個想到的方法就是枚舉 sqrt(2), sqrt(3), sqrt(4) 。。，然后sprintf出來，再比較字符串。
顯然，這種方法比較低級啦。
仔細想了下，發現如果 x.123... 這個數字的平方是一個整數的話，那必然
 sqr(x.124) > ceil(sqr(x.123))  [sqr = 求平方, ceil = 向上取整]
所以，就可以從小到大枚舉它的整數部分 x ，遇到第一個滿足結果的 x，就是答案了。


代碼 0ms AC

#include <stdio.h>
#include <math.h>

double A, P, B;
int L;

__inline double sqr(double i)
{
    return i * i;
}

double pow_1[] = {
    1, 1e-1, 1e-2, 1e-3, 1e-4, 1e-5, 1e-6, 1e-7, 1e-8, 1e-9, 1e-10, 
};

int main()
{
    double i, j;
    int d;

    freopen("e:\\test\\in.txt", "r", stdin);

    scanf("%d%d", &L, &d);
    P = pow_1[L];
    B = P * d;
    for (A = 1; ; A++) {
        i = (__int64)sqr(A + B) + 1;
        j = sqr(A + B + P);
        if (j > i)
            break;
    }
    printf("%I64d\n", (__int64)i);

    return 0;
}

     摘要: 這個題目立意很好，但是就是數據比較無語了。O(N^3)的算法都能跑得比 O(N^2LgN)的快。代碼寫很長，這份應該算比較爛了，連自己都不知道代碼的時間復雜度是多少！最終170ms AC，速度不快，比幾百行的O(N^3)代碼要慢很多。。。注意：用分數保存斜率，可以不觸及精度問題，而且還比較方便。提交了很多次都WA，不知道問題所在，于是還寫了一個腳本來測數據，然后發現了問題所在。附帶腳本和測試數據...  閱讀全文

有人說，宮崎駿只拍過一部片子，叫做《我們的純真與失落》。

思路：
開四個樹狀數組。。
arr_x，arr_y，arr_xy，arr_cnt
分別統計y軸下：x的和、y的和、x*y的和、點的個數。
把點按照x排序，x越大的點出現得越晚。
從前往后推，每出現一個新的點的時候：
Step1，將該點加入到四個數組中。
Step2，對于高于它的點，面積增量為 x*sum(y) - sum(x*y)。
Step3，對于低于它的點，面積增量為 sum(y) * (cnt * x - sum(x))
最終得出結果。復雜度O(NlgN)。代碼 63ms。

注意：
需要用int64保存數組元素

思路：
如果之前出現過長度為 len 的子序列。假設該子序列出現在 [a, b] 之間。
那如果存在 1, 2, ... K 任意一個數字出現在 [a, b] 之間，則必然存在一個長度為 len + 1 的非子序列。

代碼：
從后往前推。用的是鏈表。94ms AC。
速度一般，還是不知道那些 0ms 是怎么搞出來的。
有人說可以從前往后推，可能會快一點吧。

#include <stdio.h>

#define MAX_N 100032
#define MAX_K 10032

struct node {
    int idx;
    struct node *next;
};
struct node nodes[MAX_N], *pos[MAX_K];
int N, K, left;

int main()
{
    int i, j, len;

    freopen("e:\\test\\in.txt", "r", stdin);
    
    scanf("%d%d", &N, &K);
    for (i = 0; i < N; i++) {
        scanf("%d", &j);
        nodes[i].idx = i;
        nodes[i].next = pos[j];
        pos[j] = &nodes[i];
    }

    left = N + 1;
    for (len = 1; len <= N; len++) {
        j = left;
        for (i = 1; i <= K; i++) {
            while (pos[i] && pos[i]->idx >= left)
                pos[i] = pos[i]->next;
            if (!pos[i])
                break;
            if (pos[i]->idx < j)
                j = pos[i]->idx;
        }
        if (i <= K)
            break;
        left = j;
    }
    printf("%d\n", len);

    return 0;
}

思路：
首先每條路徑的值都可以分解一下質因數，就可以表示為多個質數的冪相乘的形式，
 比如 2^6 * 3^8 * 17^22 * 23^1。

三個數字a, b, c求最大公約數，分解完質因數后：
如果a擁有2^8，b擁有2^10，c擁有2^4。那最大公約數必然擁有2^4，取最小的一個。
對于每個質數 2, 3, 5, 7。。都是這個道理。

如果是求最小公倍數，在剛剛的例子里，就是取最大的一個了。

在點之間行走的過程，可以這樣來看。在點1的時候GCF的值是所有質數的最大次冪的乘積。
GCF的值必定是越走越小。
每經過一條路徑，CGF各個質因數的冪都必須小于等于路徑的對應的值。
就好比路徑就只能容納這么大的流量。然后到達點2的時候，看看哪條路徑的流量最大。
看起來像最大流問題，但不是最大流問題。

我們沒辦法遍歷一次圖，就求出哪條路徑的流量最大。
但由于路徑的權值最大才2000，質因數的冪最大也只有11（2^11 = 2048），大不了每個冪都試一次。
用二分法就可以了。

對于每一個質數，求到達點2 的時候的最大的冪。
最后再乘起來，就是答案了。
可見這種方法還是很巧妙的，效率也很高，0ms AC。

注意：
不需要高精度。但需要用__int64來保存答案。