|
|
思路: 這題目非常牛逼!是道月賽的題目!看完題目我就放棄了。。直接看解題報告。 解法果然牛逼! 解題報告鏈接在此: http://acm.pku.edu.cn/JudgeOnline/images/contestreport/200606/G.htm代碼是照著解題報告寫的,不過還是很爛,好像3000+ms,實在佩服那些1000ms內的神牛們!
 #include <stdio.h> #include <stdio.h>

 #define MAX_N 1024 #define MAX_N 1024

  struct queue_node struct queue_node  { {
 int y, x; int y, x;
 }; };

 int set[MAX_N][MAX_N], cut[MAX_N][MAX_N]; int set[MAX_N][MAX_N], cut[MAX_N][MAX_N];
 int N, M; int N, M;
 int left, top, right, bottom; int left, top, right, bottom;

 struct queue_node queue[MAX_N * MAX_N]; struct queue_node queue[MAX_N * MAX_N];
 int head, tail; int head, tail;

 inline int find(int *arr, int idx) inline int find(int *arr, int idx)
   { {
 static int stk[MAX_N * MAX_N], sp; static int stk[MAX_N * MAX_N], sp;

 for (sp = 0; arr[idx]; idx = arr[idx]) for (sp = 0; arr[idx]; idx = arr[idx])
 stk[sp++] = idx; stk[sp++] = idx;
 for (sp--; sp >= 0; sp--) for (sp--; sp >= 0; sp--)
 arr[stk[sp]] = idx; arr[stk[sp]] = idx;

 return idx; return idx;
 } }

 inline void push(int y, int x) inline void push(int y, int x)
   { {
 if (x < left || x > right || y < top || y > bottom) if (x < left || x > right || y < top || y > bottom)
 return ; return ;
 if (cut[y][x]) if (cut[y][x])
 return ; return ;

 cut[y][x] = 1; cut[y][x] = 1;
  if (cut[y][x - 1] && cut[y][x + 1]) if (cut[y][x - 1] && cut[y][x + 1])  { {
 set[y][x] = x + 1; set[y][x] = x + 1;
 set[y][x - 1] = x + 1; set[y][x - 1] = x + 1;
 } else if (cut[y][x - 1]) } else if (cut[y][x - 1])
 set[y][x - 1] = x; set[y][x - 1] = x;
 else if (cut[y][x + 1]) else if (cut[y][x + 1])
 set[y][x] = x + 1; set[y][x] = x + 1;

 queue[tail].y = y; queue[tail].y = y;
 queue[tail].x = x; queue[tail].x = x;
 tail++; tail++;
 } }

 inline int bfs(int y, int x) inline int bfs(int y, int x)
   { {
 x = find(set[y], x); x = find(set[y], x);
 if (cut[y][x]) if (cut[y][x])
 x++; x++;
 if (x > right) if (x > right)
 return 0; return 0;

 head = tail = 0; head = tail = 0;
 push(y, x); push(y, x);
  while (head != tail) while (head != tail)  { {
 y = queue[head].y; y = queue[head].y;
 x = queue[head].x; x = queue[head].x;
 head++; head++;
 push(y - 1, x); push(y - 1, x);
 push(y + 1, x); push(y + 1, x);
 push(y, x - 1); push(y, x - 1);
 push(y, x + 1); push(y, x + 1);
 } }

 return 1; return 1;
 } }

 int main() int main()
   { {
 int i, j, ans; int i, j, ans;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d", &N, &M); scanf("%d%d", &N, &M);
  while (M--) while (M--)  { {
 scanf("%d%d%d%d", &left, &top, &right, &bottom); scanf("%d%d%d%d", &left, &top, &right, &bottom);
 ans = 0; ans = 0;
 for (i = top; i <= bottom; i++) for (i = top; i <= bottom; i++)
 while (bfs(i, left)) while (bfs(i, left))
 ans++; ans++;
 printf("%d\n", ans); printf("%d\n", ans);
 } }

 return 0; return 0;
 } }

思路:
狀態數組 f[N][B][2]:
f[i][j][0] = { 現在處于第 i 個小時,之前一共休息了 j 個小時,第 i 個小時休息了。到現在為止獲得的最大點數 }
f[i][j][1] = { 現在處于第 i 個小時,之前一共休息了 j 個小時,第 i 個小時沒休息。到現在為止獲得的最大點數 }
由于是循環數組。所以就分開兩種情況:
1. 第 1 個小時沒休息
2. 第 1 個小時休息了
 #include <stdio.h> #include <stdio.h>
 #include <string.h> #include <string.h>
 #include <stdlib.h> #include <stdlib.h>

 #define MAX_N 4096 #define MAX_N 4096

 int in[MAX_N], N, B; int in[MAX_N], N, B;
 int dp[2][MAX_N][2], (*cur)[2], (*pre)[2]; int dp[2][MAX_N][2], (*cur)[2], (*pre)[2];

 __inline int max(int a, int b) __inline int max(int a, int b)
   { {
 return a > b ? a : b; return a > b ? a : b;
 } }

 int main() int main()
   { {
 int i, j, val; int i, j, val;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d", &N, &B); scanf("%d%d", &N, &B);
 for (i = 0; i < N; i++) for (i = 0; i < N; i++)
 scanf("%d", &in[i]); scanf("%d", &in[i]);

 // not using period #1 // not using period #1
  for (i = 2; i < N; i++) for (i = 2; i < N; i++)  { {
 pre = dp[i & 1]; pre = dp[i & 1];
 cur = dp[(i + 1) & 1]; cur = dp[(i + 1) & 1];
  for (j = B - 2; j >= 0; j--) for (j = B - 2; j >= 0; j--)  { {
 cur[j][1] = max(pre[j + 1][1] + in[i], pre[j + 1][0]); cur[j][1] = max(pre[j + 1][1] + in[i], pre[j + 1][0]);
 cur[j][0] = max(pre[j][1], pre[j][0]); cur[j][0] = max(pre[j][1], pre[j][0]);
 } }
 } }
 val = max(cur[0][1], cur[0][0]); val = max(cur[0][1], cur[0][0]);

 // using period #1 // using period #1
 memset(dp, 0, sizeof(dp)); memset(dp, 0, sizeof(dp));
 pre = dp[0]; pre = dp[0];
 pre[B - 2][1] = in[1]; pre[B - 2][1] = in[1];
  for (i = 2; i < N; i++) for (i = 2; i < N; i++)  { {
 pre = dp[i & 1]; pre = dp[i & 1];
 cur = dp[(i + 1) & 1]; cur = dp[(i + 1) & 1];
  for (j = B - 2; j >= 0; j--) for (j = B - 2; j >= 0; j--)  { {
 cur[j][1] = j == B - 2 ? 0 : max(pre[j + 1][1] + in[i], pre[j + 1][0]); cur[j][1] = j == B - 2 ? 0 : max(pre[j + 1][1] + in[i], pre[j + 1][0]);
 if (i == N - 1) if (i == N - 1)
 cur[j][1] += in[0]; cur[j][1] += in[0];
 cur[j][0] = max(pre[j][1], pre[j][0]); cur[j][0] = max(pre[j][1], pre[j][0]);
 } }
 } }
 val = max(val, cur[0][1]); val = max(val, cur[0][1]);
 val = max(val, cur[0][0]); val = max(val, cur[0][0]);

 printf("%d\n", val); printf("%d\n", val);

 return 0; return 0;
 } }

摘要: 這題看了以后,想了一個很腦殘的做法,也過了,不過用了1.2s,哈哈。后來看了一個高中生大牛寫的 Pascal 程序。根據函數名字來看,它用的是 floodfill 算法,提交了發現居然才用了188ms。現在高中生真太牛逼了!佩服!同時,作為一個即將畢業的大學生,哥表示壓力很大。。以前沒見過這個算法,看了一下,發現看不大懂,但是這樣做確實很有道理!在網上面搜了一下關于floodfill算法的資料,發... 閱讀全文
用鄰接表存邊,需要記錄路徑。
 #include <stdio.h> #include <stdio.h>

 #define MAX_N 50032 #define MAX_N 50032
 #define MAX_K 1024 #define MAX_K 1024

  struct queue_node struct queue_node  { {
 int step, idx; int step, idx;
 struct queue_node *prev; struct queue_node *prev;
 }; };
 struct queue_node queue[MAX_K]; struct queue_node queue[MAX_K];

  struct edge_node struct edge_node  { {
 int idx; int idx;
 struct edge_node *next; struct edge_node *next;
 }; };
 struct edge_node edges[MAX_N], *map[MAX_K]; struct edge_node edges[MAX_N], *map[MAX_K];

 int qh, qt, N, K, visited[MAX_K], path[MAX_K]; int qh, qt, N, K, visited[MAX_K], path[MAX_K];

 __inline int push(int idx, int step, struct queue_node *prev) __inline int push(int idx, int step, struct queue_node *prev)
   { {
 if (visited[idx]) if (visited[idx])
 return 0; return 0;
 visited[idx]++; visited[idx]++;
 queue[qt].idx = idx; queue[qt].idx = idx;
 queue[qt].step = step; queue[qt].step = step;
 queue[qt].prev = prev; queue[qt].prev = prev;
 qt++; qt++;
 return idx == K; return idx == K;
 } }

 int main() int main()
   { {
 int i, a, b; int i, a, b;
 struct queue_node *t; struct queue_node *t;
 struct edge_node *e; struct edge_node *e;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d", &N, &K); scanf("%d%d", &N, &K);
  for (i = 0; i < N; i++) for (i = 0; i < N; i++)  { {
 scanf("%d%d", &a, &b); scanf("%d%d", &a, &b);
 edges[i].idx = b; edges[i].idx = b;
 edges[i].next = map[a]; edges[i].next = map[a];
 map[a] = &edges[i]; map[a] = &edges[i];
 } }

 push(1, 1, NULL); push(1, 1, NULL);
  while (qh != qt) while (qh != qt)  { {
 t = &queue[qh++]; t = &queue[qh++];
 for (e = map[t->idx]; e; e = e->next) for (e = map[t->idx]; e; e = e->next)
 if (push(e->idx, t->step + 1, t)) if (push(e->idx, t->step + 1, t))
 break; break;
 if (e) if (e)
 break; break;
 } }

  if (qh == qt) if (qh == qt)  { {
 printf("-1\n"); printf("-1\n");
 return 0; return 0;
 } }

 t = &queue[--qt]; t = &queue[--qt];
 printf("%d\n", t->step); printf("%d\n", t->step);
 for (i = 0; t; t = t->prev) for (i = 0; t; t = t->prev)
 path[i++] = t->idx; path[i++] = t->idx;
 for (i--; i >= 0; i--) for (i--; i >= 0; i--)
 printf("%d\n", path[i]); printf("%d\n", path[i]);

 return 0; return 0;
 } }


思路:
首先對所有位置排序一下。
可能的最大的 distance 為 (range_right - range_left) / (C - 1)。
所以二分答案的時候區間的右邊就是這個了。
判斷某個 distance 是否能夠成立的過程很簡單:
只需要從左往右放牛,如果放到最后一個點都放不完,就不成立了。
代碼 140ms:
 #include <stdio.h> #include <stdio.h>
 #include <stdlib.h> #include <stdlib.h>

 int N, C, in[100032]; int N, C, in[100032];

 int cmp(const void *a, const void *b) int cmp(const void *a, const void *b)
   { {
 return *(int *)a - *(int *)b; return *(int *)a - *(int *)b;
 } }

 __inline int can(int val) __inline int can(int val)
   { {
 int i, pos, sum; int i, pos, sum;

 pos = 1; pos = 1;
  for (i = 1; i < C; i++) for (i = 1; i < C; i++)  { {
 sum = 0; sum = 0;
  while (pos < N && sum < val) while (pos < N && sum < val)  { {
 sum += in[pos] - in[pos - 1]; sum += in[pos] - in[pos - 1];
 pos++; pos++;
 } }
 if (sum < val) if (sum < val)
 return 0; return 0;
 } }
 return 1; return 1;
 } }

 int main() int main()
   { {
 int i, l, r, m; int i, l, r, m;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d", &N, &C); scanf("%d%d", &N, &C);
 for (i = 0; i < N; i++) for (i = 0; i < N; i++)
 scanf("%d", &in[i]); scanf("%d", &in[i]);
 qsort(in, N, sizeof(in[0]), cmp); qsort(in, N, sizeof(in[0]), cmp);

 l = 0; l = 0;
 r = (in[N - 1] - in[0]) / (C - 1); r = (in[N - 1] - in[0]) / (C - 1);
  while (l <= r) while (l <= r)  { {
 m = (l + r) / 2; m = (l + r) / 2;
 if (can(m)) if (can(m))
 l = m + 1; l = m + 1;
 else else
 r = m - 1; r = m - 1;
 } }
 printf("%d\n", r); printf("%d\n", r);

 return 0; return 0;
 } }

思路:
首先按照 J牛 的數量排序,最小的前 K 個肯定是一個組了。反正這組都是輸的,多爛都行。
剩下的 2K 個元素,和肯定是超過 2K*500 的。問題就是要劃分一下,讓每個組的和都大于 K*500。
這里沒有說一定要平均分,也沒說要滿足什么其他特殊條件,而且數據又特別小。
所以就可以隨機的分別挑選兩個元素交換,然后看是否滿足條件了。
代碼居然 0MS AC了,隨機的威力很大啊,只是不可能題題都用罷了。。
 #include <stdio.h> #include <stdio.h>
 #include <stdlib.h> #include <stdlib.h>
 #include <math.h> #include <math.h>

 int K, in[256], *ptr[256]; int K, in[256], *ptr[256];

 int cmp(const void *a, const void *b) int cmp(const void *a, const void *b)
   { {
 return *(*(int **)a) - *(*(int **)b); return *(*(int **)a) - *(*(int **)b);
 } }

 __inline void swap(int **a, int **b) __inline void swap(int **a, int **b)
   { {
 int *t = *a; int *t = *a;
 *a = *b; *a = *b;
 *b = t; *b = t;
 } }

 int main() int main()
   { {
 int i, sa, sb, a, b; int i, sa, sb, a, b;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d", &K); scanf("%d", &K);
  for (i = 0; i < 3*K; i++) for (i = 0; i < 3*K; i++)  { {
 scanf("%d", &in[i]); scanf("%d", &in[i]);
 ptr[i] = &in[i]; ptr[i] = &in[i];
 } }
 qsort(ptr, 3*K, sizeof(ptr[0]), cmp); qsort(ptr, 3*K, sizeof(ptr[0]), cmp);

 sa = 0; sa = 0;
 for (i = K; i < 2*K; i++) for (i = K; i < 2*K; i++)
 sa += *ptr[i]; sa += *ptr[i];
 sb = 0; sb = 0;
 for (i = 2*K; i < 3*K; i++) for (i = 2*K; i < 3*K; i++)
 sb += *ptr[i]; sb += *ptr[i];
  while (1) while (1)  { {
 a = (rand() % K) + K; a = (rand() % K) + K;
 b = (rand() % K) + 2*K; b = (rand() % K) + 2*K;
 sa = sa - *ptr[a] + *ptr[b]; sa = sa - *ptr[a] + *ptr[b];
 sb = sb - *ptr[b] + *ptr[a]; sb = sb - *ptr[b] + *ptr[a];
 swap(&ptr[a], &ptr[b]); swap(&ptr[a], &ptr[b]);
 if (sa > 500*K && sb > 500*K) if (sa > 500*K && sb > 500*K)
 break; break;
 } }

 for (i = 0; i < 3*K; i++) for (i = 0; i < 3*K; i++)
 printf("%d\n", ptr[i] - in + 1); printf("%d\n", ptr[i] - in + 1);

 return 0; return 0;
 } }

思路: 一次寬搜就可以解決了。 每個搜索節點需要保存一個 stat 值:如果攜帶了 shrubbery 則 stat = 1。否則為 0。
地圖上的每個點也保存一個 stat 值:如果沒經過則stat = 0;如果空著手經過則stat = 1;如果帶著 shrubbery經過則stat = 2。判重的時候,如果地圖的 stat 值大于搜索節點的 stat 值就可以忽略了。 代碼 266ms:
 #include <stdio.h> #include <stdio.h>

 #define SIZE 1024 #define SIZE 1024

  struct map_node struct map_node  { {
 int type, stat; int type, stat;
 }; };
 struct map_node map[SIZE][SIZE]; struct map_node map[SIZE][SIZE];

  struct queue_node struct queue_node  { {
 int step, x, y, stat; int step, x, y, stat;
 }; };
 struct queue_node queue[SIZE * SIZE * 2]; struct queue_node queue[SIZE * SIZE * 2];

 int W, H, qh, qt; int W, H, qh, qt;

 __inline int push(int y, int x, int stat, int step) __inline int push(int y, int x, int stat, int step)
   { {
 if (y < 0 || y >= H || x < 0 || x >= W) if (y < 0 || y >= H || x < 0 || x >= W)
 return 0; return 0;
 if (map[y][x].type == 1) if (map[y][x].type == 1)
 return 0; return 0;
 if (map[y][x].type == 3) if (map[y][x].type == 3)
 return stat; return stat;
 if (map[y][x].type == 4) if (map[y][x].type == 4)
 stat = 1; stat = 1;
 if (map[y][x].stat > stat) if (map[y][x].stat > stat)
 return 0; return 0;

 map[y][x].stat++; map[y][x].stat++;
 queue[qt].stat = stat; queue[qt].stat = stat;
 queue[qt].y = y; queue[qt].y = y;
 queue[qt].x = x; queue[qt].x = x;
 queue[qt].step = step; queue[qt].step = step;
 qt++; qt++;

 return 0; return 0;
 } }

 int main() int main()
   { {
 int i, j; int i, j;
 struct queue_node *t; struct queue_node *t;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 t = &queue[qt++]; t = &queue[qt++];
 scanf("%d%d", &W, &H); scanf("%d%d", &W, &H);
  for (i = 0; i < H; i++) for (i = 0; i < H; i++)  { {
  for (j = 0; j < W; j++) for (j = 0; j < W; j++)  { {
 scanf("%d", &map[i][j].type); scanf("%d", &map[i][j].type);
  if (map[i][j].type == 2) if (map[i][j].type == 2)  { {
 t->y = i; t->y = i;
 t->x = j; t->x = j;
 } }
 } }
 } }

  while (qh != qt) while (qh != qt)  { {
 t = &queue[qh++]; t = &queue[qh++];
 if (push(t->y - 1, t->x, t->stat, t->step + 1) || if (push(t->y - 1, t->x, t->stat, t->step + 1) ||
 push(t->y + 1, t->x, t->stat, t->step + 1) || push(t->y + 1, t->x, t->stat, t->step + 1) ||
 push(t->y, t->x - 1, t->stat, t->step + 1) || push(t->y, t->x - 1, t->stat, t->step + 1) ||
 push(t->y, t->x + 1, t->stat, t->step + 1) push(t->y, t->x + 1, t->stat, t->step + 1)
 ) )
 break; break;
 } }
 printf("%d\n", t->step + 1); printf("%d\n", t->step + 1);

 return 0; return 0;
 } }

這題目真的把人雷了!
題目看上去是最簡單的那種01背包,但范圍是 2^30 特別大,所以必然就不能用背包來做,只能搜索。
題目說 N <= 1000,還說輸入的數據中,一個數大于它前面兩個數的和。
所以就一直在想,是不是能利用這種特性來做些什么,但是思考了很久,無果。
看到題目 1400 / 300 的通過率,就認定這是一道難題了,基本做不出來了。
于是就直接看了下數據,發現 N 最大才 40 !
寫了一個很簡單的搜索,0ms 就過了。被瞬間雷倒了!
為什么這道題要這樣整蠱人呢?
看到 Discuss 里面有人提到“斐波那契數列”。忽然發現,題目的數據不就是跟“斐波那契”差不多嗎!
只不過增長的還要快一點。
寫了個程序測了下,發現第 46 項的和就已經超過 2^30 了。瞬間又無語了。
所以這題目確實是一道牛題!
 #include <stdio.h> #include <stdio.h>
 #include <math.h> #include <math.h>

 int detect_range() int detect_range()
   { {
 double f, n; double f, n;

  for (n = 1; n < 100; n++) for (n = 1; n < 100; n++)  { {
 f = pow(((sqrt(5.0) + 1) / 2), n); f = pow(((sqrt(5.0) + 1) / 2), n);
 printf("%d -> %lf\n", (int)n, f); printf("%d -> %lf\n", (int)n, f);
 if ((int)f > (1 << 30)) if ((int)f > (1 << 30))
 break; break;
 } }

 return 0; return 0;
 } }

 #define MAX_N 64 #define MAX_N 64

 __int64 sum[MAX_N], data[MAX_N], min_val, C; __int64 sum[MAX_N], data[MAX_N], min_val, C;
 int N; int N;

 void dfs(int idx) void dfs(int idx)
   { {
 while (idx > 0 && data[idx] > C) while (idx > 0 && data[idx] > C)
 idx--; idx--;
  while (idx > 0 && sum[idx] >= C) while (idx > 0 && sum[idx] >= C)  { {
 C -= data[idx]; C -= data[idx];
 dfs(idx - 1); dfs(idx - 1);
 C += data[idx]; C += data[idx];
 dfs(idx - 1); dfs(idx - 1);
 idx--; idx--;
 } }
 if (C - sum[idx] < min_val) if (C - sum[idx] < min_val)
 min_val = C - sum[idx]; min_val = C - sum[idx];
 } }

 int main() int main()
   { {
 int i; int i;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%I64d", &N, &C); scanf("%d%I64d", &N, &C);
  for (i = 1; i <= N; i++) for (i = 1; i <= N; i++)  { {
 scanf("%I64d", &data[i]); scanf("%I64d", &data[i]);
 sum[i] = sum[i - 1] + data[i]; sum[i] = sum[i - 1] + data[i];
 } }
 min_val = C; min_val = C;
 while (data[N] > C) while (data[N] > C)
 N--; N--;
 dfs(N); dfs(N);
 printf("%I64d\n", C - min_val); printf("%I64d\n", C - min_val);

 return 0; return 0;
 } }


這題看似挺有實際用途的,呵呵。
大意就是用最小的花費覆蓋一段區間。
思路:
動態規劃,就是說,將線段的左端點從左到右排序。依次處理:
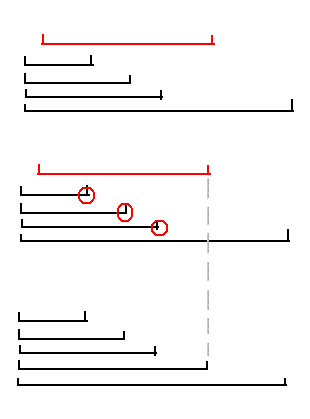 1. 假設已經知道,所有的短線拼接起來之后,能組成哪幾條長線(M為左端點)。 2. 當我們放入一條短線的時候,它能夠和舊長線繼續拼接。這時候,我們需要選取花費最小的那條。 3. 拼接之后,生成一條新的長線。 在(2)中,“選取花費最小的那條”可以用線段樹來實現。也就是求區間內的最小值,RMQ問題,由于只插入不刪除,線段樹是可以維護的。 就這樣一直處理,最終答案就是花費最小的以E為右端點的長線。 代碼 94MS:
 #include <stdio.h> #include <stdio.h>
 #include <stdlib.h> #include <stdlib.h>

 #ifndef INT_MAX #ifndef INT_MAX
 #define INT_MAX 0x7fffffff #define INT_MAX 0x7fffffff
 #endif #endif

  struct tree_node struct tree_node  { {
 int cnt, min; int cnt, min;
 }; };
  struct seg_node struct seg_node  { {
 int a, b, s; int a, b, s;
 }; };
 int N, M, E; int N, M, E;
 struct tree_node tree[86432 * 4]; struct tree_node tree[86432 * 4];
 struct seg_node in[10032]; struct seg_node in[10032];

 int cmp(const void *a, const void *b) int cmp(const void *a, const void *b)
   { {
 return ((struct seg_node *)a)->a - ((struct seg_node *)b)->a; return ((struct seg_node *)a)->a - ((struct seg_node *)b)->a;
 } }

 __inline int max(int a, int b) __inline int max(int a, int b)
   { {
 return a > b ? a : b; return a > b ? a : b;
 } }

 __inline int min(int a, int b) __inline int min(int a, int b)
   { {
 return a < b ? a : b; return a < b ? a : b;
 } }

 void tree_op(const int ins, void tree_op(const int ins,
 int idx, int idx,
 int left, int right, int left, int right,
 int start, int end, int start, int end,
 int *val int *val
 ) )
   { {
 int mid; int mid;

  if (ins) if (ins)  { {
 if (!tree[idx].cnt || *val < tree[idx].min) if (!tree[idx].cnt || *val < tree[idx].min)
 tree[idx].min = *val; tree[idx].min = *val;
 tree[idx].cnt++; tree[idx].cnt++;
 } }

  if (left == start && right == end) if (left == start && right == end)  { {
 if (!ins && tree[idx].cnt && tree[idx].min < *val) if (!ins && tree[idx].cnt && tree[idx].min < *val)
 *val = tree[idx].min; *val = tree[idx].min;
 return ; return ;
 } }

 mid = (left + right) / 2; mid = (left + right) / 2;
 if (end <= mid) if (end <= mid)
 tree_op(ins, idx*2, left, mid, start, end, val); tree_op(ins, idx*2, left, mid, start, end, val);
 else if (start > mid) else if (start > mid)
 tree_op(ins, idx*2 + 1, mid + 1, right, start, end, val); tree_op(ins, idx*2 + 1, mid + 1, right, start, end, val);
  else else  { {
 tree_op(ins, idx*2, left, mid, start, mid, val); tree_op(ins, idx*2, left, mid, start, mid, val);
 tree_op(ins, idx*2 + 1, mid + 1, right, mid + 1, end, val); tree_op(ins, idx*2 + 1, mid + 1, right, mid + 1, end, val);
 } }
 } }

 int main() int main()
   { {
 int i, val, start, end; int i, val, start, end;

 freopen("e:\\test\\in.txt", "r", stdin); freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d%d", &N, &M, &E); scanf("%d%d%d", &N, &M, &E);
 for (i = 0; i < N; i++) for (i = 0; i < N; i++)
 scanf("%d%d%d", &in[i].a, &in[i].b, &in[i].s); scanf("%d%d%d", &in[i].a, &in[i].b, &in[i].s);
 qsort(in, N, sizeof(in[0]), cmp); qsort(in, N, sizeof(in[0]), cmp);

  for (i = 0; i < N; i++) for (i = 0; i < N; i++)  { {
 if (in[i].b < M) if (in[i].b < M)
 continue; continue;
 if (in[i].a > E) if (in[i].a > E)
 break; break;
 start = max(M, in[i].a - 1); start = max(M, in[i].a - 1);
 end = min(E, in[i].b); end = min(E, in[i].b);
  if (in[i].a == M) if (in[i].a == M)  { {
 tree_op(1, 1, M, E, end, end, &in[i].s); tree_op(1, 1, M, E, end, end, &in[i].s);
 continue; continue;
 } }
 val = INT_MAX; val = INT_MAX;
 tree_op(0, 1, M, E, start, end, &val); tree_op(0, 1, M, E, start, end, &val);
 if (val == INT_MAX) if (val == INT_MAX)
 continue; continue;
 val += in[i].s; val += in[i].s;
 tree_op(1, 1, M, E, end, end, &val); tree_op(1, 1, M, E, end, end, &val);
 } }

 val = INT_MAX; val = INT_MAX;
 tree_op(0, 1, M, E, E, E, &val); tree_op(0, 1, M, E, E, E, &val);
 printf("%d\n", val == INT_MAX ? -1 : val); printf("%d\n", val == INT_MAX ? -1 : val);

 return 0; return 0;
 } }

摘要: 思路:由于數據量比較小,可以枚舉ABCDE的所有身份和時間(白天或者晚上),不會超時。判斷deducible、impossible的部分很難寫,基本上是照著數據改的。。1. 如果沒有任何狀態是符合要求的,輸出 impossible。2. 在符合要求的狀態中,如果對于某個人的身份或者時間,存在分歧,那該條就不能輸出。3. 在(2)的情況下,如果沒有任何輸出,就輸出 deducible。快被這玩意整瘋... 閱讀全文
|
 #include <stdio.h>
#include <stdio.h>
 #define MAX_N 1024
#define MAX_N 1024

 struct queue_node
struct queue_node  {
{ int y, x;
int y, x; };
};
 int set[MAX_N][MAX_N], cut[MAX_N][MAX_N];
int set[MAX_N][MAX_N], cut[MAX_N][MAX_N]; int N, M;
int N, M; int left, top, right, bottom;
int left, top, right, bottom;
 struct queue_node queue[MAX_N * MAX_N];
struct queue_node queue[MAX_N * MAX_N]; int head, tail;
int head, tail;
 inline int find(int *arr, int idx)
inline int find(int *arr, int idx)

 {
{ static int stk[MAX_N * MAX_N], sp;
static int stk[MAX_N * MAX_N], sp;
 for (sp = 0; arr[idx]; idx = arr[idx])
for (sp = 0; arr[idx]; idx = arr[idx]) stk[sp++] = idx;
stk[sp++] = idx; for (sp--; sp >= 0; sp--)
for (sp--; sp >= 0; sp--) arr[stk[sp]] = idx;
arr[stk[sp]] = idx;
 return idx;
return idx; }
}
 inline void push(int y, int x)
inline void push(int y, int x)

 {
{ if (x < left || x > right || y < top || y > bottom)
if (x < left || x > right || y < top || y > bottom) return ;
return ; if (cut[y][x])
if (cut[y][x]) return ;
return ;
 cut[y][x] = 1;
cut[y][x] = 1;
 if (cut[y][x - 1] && cut[y][x + 1])
if (cut[y][x - 1] && cut[y][x + 1])  {
{ set[y][x] = x + 1;
set[y][x] = x + 1; set[y][x - 1] = x + 1;
set[y][x - 1] = x + 1; } else if (cut[y][x - 1])
} else if (cut[y][x - 1])  set[y][x - 1] = x;
set[y][x - 1] = x; else if (cut[y][x + 1])
else if (cut[y][x + 1]) set[y][x] = x + 1;
set[y][x] = x + 1;
 queue[tail].y = y;
queue[tail].y = y; queue[tail].x = x;
queue[tail].x = x; tail++;
tail++; }
}
 inline int bfs(int y, int x)
inline int bfs(int y, int x)

 {
{ x = find(set[y], x);
x = find(set[y], x); if (cut[y][x])
if (cut[y][x]) x++;
x++; if (x > right)
if (x > right) return 0;
return 0;
 head = tail = 0;
head = tail = 0; push(y, x);
push(y, x);
 while (head != tail)
while (head != tail)  {
{ y = queue[head].y;
y = queue[head].y; x = queue[head].x;
x = queue[head].x; head++;
head++; push(y - 1, x);
push(y - 1, x); push(y + 1, x);
push(y + 1, x); push(y, x - 1);
push(y, x - 1); push(y, x + 1);
push(y, x + 1); }
}
 return 1;
return 1; }
}
 int main()
int main()

 {
{ int i, j, ans;
int i, j, ans;
 freopen("e:\\test\\in.txt", "r", stdin);
freopen("e:\\test\\in.txt", "r", stdin);
 scanf("%d%d", &N, &M);
scanf("%d%d", &N, &M);
 while (M--)
while (M--)  {
{ scanf("%d%d%d%d", &left, &top, &right, &bottom);
scanf("%d%d%d%d", &left, &top, &right, &bottom); ans = 0;
ans = 0; for (i = top; i <= bottom; i++)
for (i = top; i <= bottom; i++) while (bfs(i, left))
while (bfs(i, left)) ans++;
ans++; printf("%d\n", ans);
printf("%d\n", ans); }
}
 return 0;
return 0; }
}

