三、有窮狀態(tài)自動(dòng)機(jī)
人閱讀正則表達(dá)式會(huì)比較簡(jiǎn)單�,但是機(jī)器閱讀正則表達(dá)式就是一件非常困難的事情了�。而且�,直接使用正則表達(dá)式進(jìn)行匹配配的話�,不僅工作量大,而且速度緩慢�。因此我們還需要另外一種專門為機(jī)器設(shè)計(jì)的表達(dá)方式�。本文在以后的章節(jié)中會(huì)給出一種算法把正則表達(dá)式轉(zhuǎn)換為機(jī)器可以閱讀的形式,就是這一章節(jié)所描述的有窮狀態(tài)自動(dòng)機(jī)�。
有窮狀態(tài)自動(dòng)機(jī)這個(gè)名字聽起來比較可怕�,不過實(shí)際上這種自動(dòng)機(jī)并沒有想象中的那么復(fù)雜�。狀態(tài)機(jī)的這種概念被廣泛的應(yīng)用在各種各樣的領(lǐng)域中。軟件工程的統(tǒng)一建模語言(UML)有狀態(tài)圖�,數(shù)字邏輯中也有狀態(tài)轉(zhuǎn)移圖�。不過這些各種各樣的圖在本質(zhì)上都跟狀態(tài)機(jī)沒有什么區(qū)別�。我將會(huì)通過一個(gè)例子來講述狀態(tài)的實(shí)際意義。
假設(shè)我們現(xiàn)在需要檢查一個(gè)字符串中a的數(shù)量和b的數(shù)量是否都是偶數(shù)�。當(dāng)然我們可以用一個(gè)正則表達(dá)式來描述它�。不過對(duì)于這個(gè)問題來說�,用正則表達(dá)式來描述遠(yuǎn)遠(yuǎn)不如構(gòu)造狀態(tài)機(jī)方便。我們可以設(shè)計(jì)出一個(gè)狀態(tài)的集合�,然后指定集合中的某一個(gè)元素為“起始狀態(tài)”�。其實(shí)狀態(tài)就是在工作還沒開始的時(shí)候�,分析器所處的狀態(tài)。分析器在每一次進(jìn)行一項(xiàng)新的工作的時(shí)候�,都要把狀態(tài)重置為起始狀態(tài)。分析器每讀入一個(gè)字符就修改一次狀態(tài),修改的方法我們也可以指定。分析器在讀完所有的字符以后�,必然停留在一個(gè)確定的狀態(tài)中�。如果這個(gè)狀態(tài)跟我們所期望的狀態(tài)一致的話�,我們就說這個(gè)分析器接受了這個(gè)字符串,否則我們就說這個(gè)分析器拒絕了這個(gè)字符串。
如何通過設(shè)計(jì)狀態(tài)及其轉(zhuǎn)移方法來實(shí)現(xiàn)一個(gè)分析器呢�?當(dāng)然�,如果一個(gè)字符串僅僅包含a或者b的話�,那么分析器的狀態(tài)只有四種:“奇數(shù)a奇數(shù)b”、“奇數(shù)a偶數(shù)b”、“偶數(shù)a奇數(shù)b”�、“偶數(shù)a偶數(shù) b”�。我們把這些狀態(tài)依次命名為aa�、aB、Ab、AB�。大寫代表偶數(shù)�,小寫代表奇數(shù)�。當(dāng)工作還沒開始的時(shí)候,分析器已經(jīng)讀入的字符串是空串,那么理所當(dāng)然的起始狀態(tài)應(yīng)當(dāng)是AB。當(dāng)分析器讀完所有字符的時(shí)候�,我們期望讀入的字符串的a和b的數(shù)量都是偶數(shù)�,那么結(jié)束的狀態(tài)也應(yīng)該是AB�。于是我們給出這樣的一個(gè)狀態(tài)圖:
圖3.1
檢查一個(gè)字符串是否由偶數(shù)個(gè)a和偶數(shù)個(gè)b組成的狀態(tài)圖
在這個(gè)狀態(tài)圖里,有一個(gè)短小的箭頭指向了AB,代表AB這個(gè)狀態(tài)是初始狀態(tài)�。AB狀態(tài)有粗的邊緣�,代表AB這個(gè)狀態(tài)是結(jié)束的可接受狀態(tài)�。一個(gè)狀態(tài)圖的結(jié)束狀態(tài)可以是一個(gè)或者多個(gè)。在這個(gè)例子里,起始狀態(tài)和結(jié)束狀態(tài)剛好是同一個(gè)狀態(tài)�。標(biāo)有字符”a”的箭頭從AB指向aB�,代表如果分析器處于狀態(tài)AB并且讀入的字符是a的話�,就轉(zhuǎn)移到狀態(tài)aB上。
我們把這個(gè)狀態(tài)圖應(yīng)用在兩個(gè)字符串上,分別是”abaabbba”和”aababbaba”�。其中�,第一個(gè)字符串是可以接受的�,第二個(gè)字符串是不可接受的(因?yàn)橛?/span>5個(gè)a和4個(gè)b)。
分析第一個(gè)字符串的時(shí)候,狀態(tài)機(jī)所經(jīng)過的狀態(tài)是:
AB[a]aB[b]ab[a]Ab[a]ab[b]aB[b]ab[b]aB[a]AB
分析第二個(gè)字符串的時(shí)候,狀態(tài)機(jī)所經(jīng)過的狀態(tài)是:
AB[a]aB[a]AB[b]Ab[a]ab[b]aB[b]ab[a]Ab[b]AB[a]aB
第一個(gè)字符串”abaabbba”讓狀態(tài)機(jī)在狀態(tài)AB上停了下來�,于是這個(gè)字符串是可以接受的�。第二個(gè)字符串”aababbaba”讓狀態(tài)機(jī)在狀態(tài)aB上停了下來�,于是這個(gè)字符串是不可以接受的。
在機(jī)器內(nèi)部表示這個(gè)狀態(tài)圖的話,我們可以使用一種比較簡(jiǎn)單的方法。這種方法僅僅把狀態(tài)與狀態(tài)之間的箭頭、起始狀態(tài)和結(jié)束狀態(tài)集合記錄下來。對(duì)應(yīng)于這個(gè)狀態(tài)圖的話,我們就可以把這個(gè)狀態(tài)圖表示成以下形式:
起始狀態(tài):AB
結(jié)束狀態(tài)集合:AB
(AB,a,aB)
(AB,b,Ab)
(aB,a,AB)
(aB,b,ab)
(Ab,a,ab)
(Ab,b,AB)
(ab,a,Ab)
(ab,b,aB)
用一個(gè)狀態(tài)圖來表示狀態(tài)機(jī)的時(shí)候有時(shí)候會(huì)遇到確定性與非確定性的問題。所謂的確定性就是指對(duì)于任何一個(gè)狀態(tài),輸入一個(gè)字符都可以跳轉(zhuǎn)到另一個(gè)確定的狀態(tài)中去�。確定性和非確定性的區(qū)別有一個(gè)直觀的描述:狀態(tài)圖的任何一個(gè)狀態(tài)都可以有不定數(shù)量的邊指向另一個(gè)狀態(tài)�,如果在這些邊里面�,存在兩條邊,它們所承載的字符如果相同,那么這個(gè)狀態(tài)輸入這個(gè)就字符可以跳轉(zhuǎn)到另外兩個(gè)狀態(tài)中去�,于是該狀態(tài)機(jī)就是不確定的�。如圖所示:
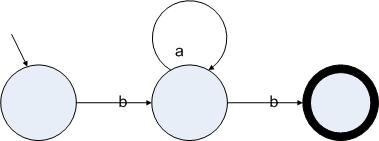
圖3.2
正則表達(dá)式ba*b的一個(gè)確定的狀態(tài)機(jī)表示
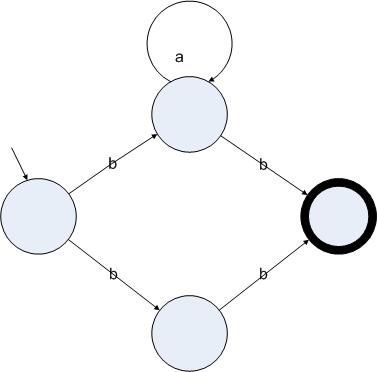
圖3.3
正則表達(dá)式ba*b的一個(gè)非確定的狀態(tài)機(jī)表示
圖3.3中的狀態(tài)機(jī)的起始狀態(tài)讀入字符b后可以跳轉(zhuǎn)到中間的兩個(gè)狀態(tài)里�,因此這個(gè)狀態(tài)機(jī)是非確定的。相反,圖3.2中的狀態(tài)機(jī)�,雖然功能跟圖3.3的狀態(tài)機(jī)一致�,但卻是確定的�。我們還可以使用一種特殊的邊來進(jìn)行狀態(tài)的轉(zhuǎn)換。我們用ε邊來表示一個(gè)狀態(tài)可以不讀入字符就跳轉(zhuǎn)到另一個(gè)狀態(tài)上。下圖給出了一個(gè)跟圖3.3功能一致的包含ε邊的非確定的狀態(tài)機(jī):
圖3.4
正則表達(dá)式ba*b的一個(gè)帶有ε邊的非確定的狀態(tài)機(jī)
在教科書中�,通常把確定的有窮狀態(tài)自動(dòng)機(jī)(有窮狀態(tài)自動(dòng)機(jī)也就是本文討論的這種狀態(tài)機(jī))稱為DFA�,把非確定的有窮狀態(tài)自動(dòng)機(jī)稱為NFA�,把帶有ε邊的非確定的狀態(tài)機(jī)稱為ε-NFA�。下文中也將采用這幾個(gè)術(shù)語來指示各種類型的有窮狀態(tài)自動(dòng)機(jī)。
在剛剛接觸到ε邊的時(shí)候�,一個(gè)通常的疑問就是這種邊存在的理由�。事實(shí)上如果是人直接畫狀態(tài)機(jī)的話�,有時(shí)候也可以直接畫出一個(gè)確定的狀態(tài)機(jī),復(fù)雜一點(diǎn)的話也可以畫出一個(gè)非確定的狀態(tài)機(jī)�,在有些極端的情況下我們需要使用ε邊來更加簡(jiǎn)潔的表示我們的意圖�。不過ε邊存在的最大的理由就是:我們可以通過使用ε邊來給出一個(gè)簡(jiǎn)潔的算法把一個(gè)正則表達(dá)式轉(zhuǎn)換成ε-NFA�。