旋轉卡殼可以用于求凸包的直徑、寬度,兩個不相交凸包間的最大距離和最小距離等。雖然算法的思想不難理解,但是實現起來真的很容易讓人“卡殼”。
拿凸包直徑(也就是凸包上最遠的兩點的距離)為例,原始的算法是這樣子:
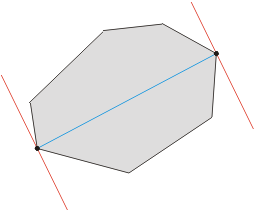
- Compute the polygon's extreme points in the y direction. Call them ymin and ymax.
- Construct two horizontal lines of support through ymin and ymax. Since this is already an anti-podal pair, compute the distance, and keep as maximum.
- Rotate the lines until one is flush with an edge of the polygon.
- A new anti-podal pair is determined. Compute the new distance, compare to old maximum, and update if necessary.
- Repeat steps 3 and 4 until the anti-podal pair considered is (ymin,ymax) again.
- Output the pair(s) determining the maximum as the diameter pair(s).
更具體的可參見http://cgm.cs.mcgill.ca/~orm/rotcal.frame.html
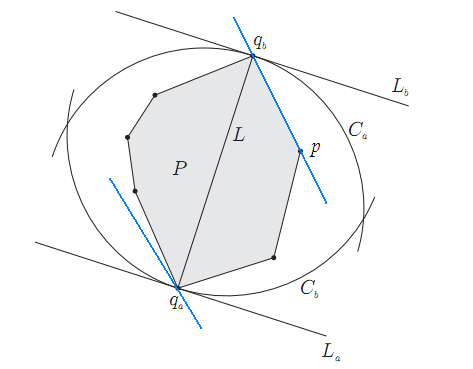
直接按照這個描述可以實現旋轉卡殼算法,但是代碼肯定相當冗長。逆向思考,如果qa,qb是凸包上最遠兩點,必然可以分別過qa,qb畫出一對平行線。通過旋轉這對平行線,我們可以讓它和凸包上的一條邊重合,如圖中藍色直線,可以注意到,qa是凸包上離p和qb所在直線最遠的點。于是我們的思路就是枚舉凸包上的所有邊,對每一條邊找出凸包上離該邊最遠的頂點,計算這個頂點到該邊兩個端點的距離,并記錄最大的值。直觀上這是一個O(n2)的算法,和直接枚舉任意兩個頂點一樣了。但是注意到當我們逆時針枚舉邊的時候,最遠點的變化也是逆時針的,這樣就可以不用從頭計算最遠點,而可以緊接著上一次的最遠點繼續計算(詳細的證明可以參見上面鏈接中的論文)。于是我們得到了O(n)的算法。
 //計算凸包直徑,輸入凸包ch,頂點個數為n,按逆時針排列,輸出直徑的平方
//計算凸包直徑,輸入凸包ch,頂點個數為n,按逆時針排列,輸出直徑的平方
 int rotating_calipers(Point *ch,int n)
int rotating_calipers(Point *ch,int n)


 {
{
 int q=1,ans=0;
int q=1,ans=0;
 ch[n]=ch[0];
ch[n]=ch[0];
 for(int p=0;p<n;p++)
for(int p=0;p<n;p++)


 {
{
 while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
 q=(q+1)%n;
q=(q+1)%n;
 ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));
ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));
 }
}
 return ans;
return ans;
 }
} 很難想象這個看起來那么麻煩的算法只有這么幾行代碼吧!其中cross函數是計算叉積,可以想成是計算三角形面積,因為凸包上距離一條邊最遠的點和這條邊的兩個端點構成的三角形面積是最大的。之所以既要更新(ch[p],ch[q])又要更新(ch[p+1],ch[q+1])是為了處理凸包上兩條邊平行的特殊情況。
poj2187要求的是平面點集上的最遠點對,實際上就是該點集的凸包的直徑。可能該題數據求得的凸包頂點數都不多,所以旋轉卡殼算法相比普通的枚舉算法并沒有明顯的優勢。完整代碼如下。

 poj2187
poj2187
 #include <cmath>
#include <cmath>
 #include <algorithm>
#include <algorithm>
 #include <iostream>
#include <iostream>
 using namespace std;
using namespace std;
 #define MAXN 50005
#define MAXN 50005

 struct Point
struct Point


 {
{
 int x, y;
int x, y;
 bool operator < (const Point& _P) const
bool operator < (const Point& _P) const


 {
{
 return y<_P.y||(y==_P.y&&x<_P.x);
return y<_P.y||(y==_P.y&&x<_P.x);
 };
};
 }pset[MAXN],ch[MAXN];
}pset[MAXN],ch[MAXN];

 void convex_hull(Point *p,Point *ch,int n,int &len)
void convex_hull(Point *p,Point *ch,int n,int &len)


 {
{
 sort(p, p+n);
sort(p, p+n);
 ch[0]=p[0];
ch[0]=p[0];
 ch[1]=p[1];
ch[1]=p[1];
 int top=1;
int top=1;
 for(int i=2;i<n;i++)
for(int i=2;i<n;i++)


 {
{
 while(top>0&&cross(ch[top],p[i],ch[top-1])<=0)
while(top>0&&cross(ch[top],p[i],ch[top-1])<=0)
 top--;
top--;
 ch[++top]=p[i];
ch[++top]=p[i];
 }
}
 int tmp=top;
int tmp=top;
 for(int i=n-2;i>=0;i--)
for(int i=n-2;i>=0;i--)


 {
{
 while(top>tmp&&cross(ch[top],p[i],ch[top-1])<=0)
while(top>tmp&&cross(ch[top],p[i],ch[top-1])<=0)
 top--;
top--;
 ch[++top]=p[i];
ch[++top]=p[i];
 }
}
 len=top;
len=top;
 }
}

 int cross(Point a,Point b,Point o)
int cross(Point a,Point b,Point o)


 {
{
 return (a.x - o.x) * (b.y - o.y) - (b.x - o.x) * (a.y - o.y);
return (a.x - o.x) * (b.y - o.y) - (b.x - o.x) * (a.y - o.y);
 }
}

 int dist2(Point a,Point b)
int dist2(Point a,Point b)


 {
{
 return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
 }
}

 int rotating_calipers(Point *ch,int n)
int rotating_calipers(Point *ch,int n)


 {
{
 int q=1,ans=0;
int q=1,ans=0;
 ch[n]=ch[0];
ch[n]=ch[0];
 for(int p=0;p<n;p++)
for(int p=0;p<n;p++)


 {
{
 while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
while(cross(ch[p+1],ch[q+1],ch[p])>cross(ch[p+1],ch[q],ch[p]))
 q=(q+1)%n;
q=(q+1)%n;
 ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));
ans=max(ans,max(dist2(ch[p],ch[q]),dist2(ch[p+1],ch[q+1])));
 }
}
 return ans;
return ans;
 }
}

 int main()
int main()


 {
{
 //freopen("in.txt","r",stdin);
//freopen("in.txt","r",stdin);
 int n, len;
int n, len;
 while(scanf("%d", &n)!=EOF)
while(scanf("%d", &n)!=EOF)


 {
{
 for(int i = 0;i < n;i++)
for(int i = 0;i < n;i++)


 {
{
 scanf("%d %d",&pset[i].x,&pset[i].y);
scanf("%d %d",&pset[i].x,&pset[i].y);
 }
}
 convex_hull(pset,ch,n,len);
convex_hull(pset,ch,n,len);
 printf("%d\n",rotating_calipers(ch,len));
printf("%d\n",rotating_calipers(ch,len));
 }
}
 return 0;
return 0;
 }
}

poj3608 要求的是兩個凸包的最近距離。這比求凸包直徑麻煩了許多。我的基本思想還是分別枚舉兩個凸包的邊,但是有些細節沒能完全證明是正確的。雖然AC了,但目前這還只是一個看起來正確的算法。這題的中間過程還需要計算點到線段的距離和兩條平行線段的距離,比起2187麻煩了許多。

 poj3608
poj3608
 #include <iostream>
#include <iostream>
 #include <algorithm>
#include <algorithm>
 #include <cmath>
#include <cmath>
 using namespace std;
using namespace std;
 #define MAXN 50000
#define MAXN 50000
 #define EPS 1e-9
#define EPS 1e-9
 struct Point
struct Point


 {
{
 double x,y;
double x,y;

 Point ()
Point () {}
{}

 Point (double _x,double _y)
Point (double _x,double _y) {x=_x;y=_y;}
{x=_x;y=_y;}
 }pm[MAXN],pn[MAXN];
}pm[MAXN],pn[MAXN];

 double cross(Point a,Point b,Point o)
double cross(Point a,Point b,Point o)


 {
{
 return (o.x-a.x)*(o.y-b.y)-(o.x-b.x)*(o.y-a.y);
return (o.x-a.x)*(o.y-b.y)-(o.x-b.x)*(o.y-a.y);
 }
}

 double dist(Point a,Point b)
double dist(Point a,Point b)


 {
{
 return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
 }
}

 double dot(Point a,Point b)
double dot(Point a,Point b)


 {
{
 return a.x*b.x+a.y*b.y;
return a.x*b.x+a.y*b.y;
 }
}

 void anticolockwise(Point *ch,int len)
void anticolockwise(Point *ch,int len)


 {
{
 for(int i=0;i<len-2;i++)
for(int i=0;i<len-2;i++)


 {
{
 double tmp=cross(ch[i],ch[i+1],ch[i+2]);
double tmp=cross(ch[i],ch[i+1],ch[i+2]);
 if(tmp>EPS)
if(tmp>EPS)
 return;
return;
 else if(tmp<-EPS)
else if(tmp<-EPS)


 {
{
 reverse(ch,ch+len);
reverse(ch,ch+len);
 return;
return;
 }
}
 }
}
 }
}

 double dis_point_to_seg(Point c,Point a,Point b)
double dis_point_to_seg(Point c,Point a,Point b)


 {
{
 Point ab=Point(b.x-a.x,b.y-a.y);
Point ab=Point(b.x-a.x,b.y-a.y);
 Point ac=Point(c.x-a.x,c.y-a.y);
Point ac=Point(c.x-a.x,c.y-a.y);
 double f=dot(ab,ac);
double f=dot(ab,ac);
 if(f<0) return dist(a,c);
if(f<0) return dist(a,c);
 double D=dot(ab,ab);
double D=dot(ab,ab);
 if(f>D) return dist(b,c);
if(f>D) return dist(b,c);
 f=f/D;
f=f/D;
 Point d=Point(a.x+f*ab.x,a.y+f*ab.y);
Point d=Point(a.x+f*ab.x,a.y+f*ab.y);
 return dist(d,c);
return dist(d,c);
 }
}

 double dis_pall_seg(Point p1, Point p2, Point p3, Point p4)
double dis_pall_seg(Point p1, Point p2, Point p3, Point p4)


 {
{
 return min(min(dis_point_to_seg(p1, p3, p4), dis_point_to_seg(p2, p3, p4)),
return min(min(dis_point_to_seg(p1, p3, p4), dis_point_to_seg(p2, p3, p4)),
 min(dis_point_to_seg(p3, p1, p2), dis_point_to_seg(p4, p1, p2)));
min(dis_point_to_seg(p3, p1, p2), dis_point_to_seg(p4, p1, p2)));
 }
}

 double rc(Point *ch1,Point *ch2,int n,int m)
double rc(Point *ch1,Point *ch2,int n,int m)


 {
{
 int q=0;
int q=0;
 int p=0;
int p=0;
 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
 if(ch1[i].y-ch1[p].y<-EPS)
if(ch1[i].y-ch1[p].y<-EPS)
 p=i;
p=i;
 for(int i=0;i<m;i++)
for(int i=0;i<m;i++)
 if(ch2[i].y-ch2[q].y>EPS)
if(ch2[i].y-ch2[q].y>EPS)
 q=i;
q=i;
 ch1[n]=ch1[0];
ch1[n]=ch1[0];
 ch2[m]=ch2[0];
ch2[m]=ch2[0];
 double tmp,ans=1e99;
double tmp,ans=1e99;
 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)


 {
{
 while((tmp=cross( ch1[p+1],ch2[q+1],ch1[p]) - cross(ch1[p+1],ch2[q],ch1[p]) )>EPS)
while((tmp=cross( ch1[p+1],ch2[q+1],ch1[p]) - cross(ch1[p+1],ch2[q],ch1[p]) )>EPS)
 q=(q+1)%m;
q=(q+1)%m;
 if(tmp<-EPS)
if(tmp<-EPS)
 ans=min(ans,dis_point_to_seg(ch2[q],ch1[p],ch1[p+1]));
ans=min(ans,dis_point_to_seg(ch2[q],ch1[p],ch1[p+1]));
 else
else
 ans=min(ans,dis_pall_seg(ch1[p],ch1[p+1],ch2[q],ch2[q+1]));
ans=min(ans,dis_pall_seg(ch1[p],ch1[p+1],ch2[q],ch2[q+1]));
 p=(p+1)%n;
p=(p+1)%n;
 }
}
 return ans;
return ans;

 }
}

 int main()
int main()


 {
{
 //freopen("in.txt","r",stdin);
//freopen("in.txt","r",stdin);
 int n,m;
int n,m;
 while(scanf("%d %d",&n,&m))
while(scanf("%d %d",&n,&m))


 {
{
 if(n==0&&m==0)
if(n==0&&m==0)
 break;
break;
 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
 scanf("%lf %lf",&pn[i].x,&pn[i].y);
scanf("%lf %lf",&pn[i].x,&pn[i].y);
 for(int i=0;i<m;i++)
for(int i=0;i<m;i++)
 scanf("%lf %lf",&pm[i].x,&pm[i].y);
scanf("%lf %lf",&pm[i].x,&pm[i].y);
 anticolockwise(pn,n);
anticolockwise(pn,n);
 anticolockwise(pm,m);
anticolockwise(pm,m);
 printf("%.5f\n",sqrt(min(rc(pn,pm,n,m),rc(pm,pn,m,n))));
printf("%.5f\n",sqrt(min(rc(pn,pm,n,m),rc(pm,pn,m,n))));
 }
}
 return 0;
return 0;
 }
}
