學弟問我的一個題目，去年本來做過，但是做的稀里糊涂，今天拿出來重新推導了一遍，特記錄于此。
　　題目鏈接：http://acm.hdu.edu.cn/showproblem.php?pid=2971
　　先假設a2 = t, 題目給定了遞推關系：An = 2 * t * An-1 - An-2 (n > 2)，初值A1 = 1, A2 = t；題目要求Sn = An ^ 2 + An-1 ^ 2 + ... + A1 ^ 2。
　　反復應用遞推關系得到：
　　
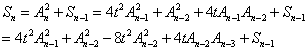
　　然后Sn-1利用相同的方式展開，把4tAn-2An-3約去，得到：
　　
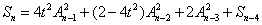
　　這樣就比較容易得出Sn的通項：
　　

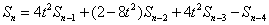
　　當初這個題目之所以沒想到這種方法，就是因為一看到遞推關系，就想著用一般解方程的方法去求解通項，思維被局限了，其實用簡單的方式就可以推出來的。以后對于一個問題，應該從多個方面去想，不能想當然啊。想起最近看到的一段話，以此自勉：
　　正則表達式非常強大，但是它并不能為每一個問題提供正確的解決方案。你應該學習足夠多的知識，以辨別什么時候它們是合適的，什么時候它們會解決你的問題，什么時候它們產生的問題比要解決的問題還要多。
　　一些人，遇到一個問題時就想：“我知道，我將使用正則表達式。”現在他有兩個問題了。——Jamie Zawinski
  Car sends me some links and data for my graduation project. It's time for me to work on it after two months vacation. I think this project is a bit difficult for me since I know little stuff about random fields. Anyway it's a good start for me, yeah, an old page has been turned over. A detailed plan will be released later on. I'm sure I'll make it!
  BTW. My English sucks, I could hardly write a whole sentence:(
     摘要: 話說ICPC的題目是越來越難，因為經典的算法大家都知道了，因此出題的方向只能是要么把模型隱藏的很深，要么就把一系列算法知識綜合起來考察，這個時候分析問題的能力和靈活運用知識的能力就顯得尤為重要。
　　polya定理在很久以前的ICPC題目中就已經出現過，不過那個時候大家對于置換群都了解不多，因此polya定理算是很生僻的一個東西。然而人類總是飛速的進步，現在互聯網上鋪天蓋地的題解使得polya定理走出深閨，逐漸被廣大acmer所熟知。但是魔高一尺道高一丈，出題人也逐漸把polya定理的題出得越來越難做，越來越不好想。  閱讀全文 【問題描述】
　　高斯消元法適用的兩種情況為域上的問題和環上的問題。域上的問題就是可以通過加減乘除把系數陣化簡成為對角線全1的形式，是允許有除法的，一般用于浮點數的高斯消元。而環上的問題一般涉及整數以及取模，除法是不允許的，此外環上的問題一般都要涉及高斯消元的一個比較難處理的問題：無窮解問題。

【問題分析】
　　首先考慮比較簡單的環上的問題：模2問題，這類問題的經典代表是開關燈問題。其實這類問題可以允許除法（用異或代替），每次消元的時候如果出現不確定的變量，那么跳過當前列，保持行不變，繼續消元。當消元過后會出現的問題是，如果系數陣的秩小于增光矩陣的秩，那么無解；或者不是所有的變量都已經取值，導致這個的原因一個是消元時出現全0列，一個是系數陣的秩等于增光矩陣的秩且小于未知數的個數，也就是出現無窮解。在模2域上出現無窮解的時候只需枚舉每個不確定變元的值（0或1），一般是用來找到一個最優解。這里一個比較巧妙的方法是保留消元過程的對角矩陣，這樣一旦確定了未知數，直接回帶找解，無需重新建立方程。
　　模n域上的無窮解問題更為復雜一些。一個是變元的取值范圍變大了（0到n-1，某些問題取值還會是負的），另一個問題是由于模n未必是素數，如果是素數存在解就一定唯一，不是素數的話會出現多組解，還得繼續枚舉才行。以幾個題目為例：
　　POJ 2947 Widget Factory：這是環上問題的基礎版，考察了對于變元數和方程數不確定的時候對方程解數的判斷方法。消元的過程還是很簡單的，細節考慮清楚就可以了。
　　POJ 1395 Cog-Wheels：方程的建立很巧妙，由于數的范圍很小（100以內），因此可以根據每個質因數的冪次建立方程！對每個輪子除以最小的那個數后就可以進行質因數分解，方程數很少；最后建立的是一個整系數方程。不過這里的問題是由于存在無窮解的情況，要搜索；而且變量的取值范圍不太好把握，我是取增廣陣的所有系數的最大值max，把枚舉的界定在了|max|以內，有點像擴展歐幾里德的思想，如果有x、y滿足ax + by = d，那么x上下浮動b個，y上下浮動a個依然方程成立。另外注意的是建立方程的時候會產生齊次方程，要特別判斷一下。總而言之這個題目寫起來很惡心，復雜度感覺巨高，但是實際運行速度很快。
　　POJ 2055 Kid's Problem：這個題目BT程度又進了一步，是個模線性方程組，不僅可能存在無窮解，而且模不一定是素數，對于確定的變元取值也會很多，總之就是各種搜索。不過這個題目很無聊的一點是在消元過程中，之前我一直是取要消元的兩個系數的最小公倍數，分別放大然后再減去，就像分數通分的做法，做其他的題目都沒有問題（因為沒有影響解的情況）；但是這個題目這樣居然會超時，當然不是超時在高斯消元的過程，而是之后枚舉的過程。這個題目必須利用那種類似求gcd的方法，兩個方程互相減來減去，因為這個題目數據取值范圍太小了（20以內），因此這樣做的復雜度也不高。這兩種做法的唯一區別就是后者消元后的對角陣中，主對角線的系數很小（減來減去減得很小），而用“通分”的方法系數會保留為原系數（可能很大），雖然最后計算的結果完全相同，但是可能后者能夠快速得到一個好的可行解，利用這個剪掉了不少冗余情況，而前者也許差了一些，就超時了。
　　Ural 1561 Winnie the Pooh：應該是高斯消元問題的終極版本了，考察的是對高斯消元的理解（不過沒有在方程的建立上設置太多的坎）。這個題目可以歸結為包含若干操作的動態高斯消元問題：添加一個變元，添加一個方程，詢問給定方程解的情況。因為不是詢問方程組的解，而是詢問方程的解，這樣的話有可能雖然有多組解但是最后對應方程的值是相同的。我一開始采用枚舉方程的取值判斷有解的方法，超時了；后來改成出現不確定解的時候搜索判斷解的情況，依然超時。這兩種方法的復雜度都達到O(n ^ 3)以上，所以需要好的辦法。仔細思考之后發現，如果方程有解且唯一，那么它一定和已經存在的方程組（看成是向量）是線性相關的，這樣的話可以每次添加方程都維護對角陣，對于一次詢問，利用已有的方程組依次對給定的方程消元，到最后判斷這個方程的系數是否全0，如果是的話解個模方程就行了，如果不是的話說明這個方程的取值會有很多種情況。每次添加方程都判斷是否產生矛盾（無解），如果無解以后不再判斷，一直輸出無解。利用這種方式可以很快的處理查詢，每次復雜度才O(n ^ 2)。

【問題總結】
　　環上的高斯消元問題應用比較廣泛，但是編碼的復雜度也比較高。此外，不同的題目往往要求各異，因此也沒有統一的模板，需要根據題目的要求來編寫程序。通過以上幾個題目的練習，對于高斯消元的求解已經沒有太大的問題了。但是題目中方程的建立以及優化求解依然是難點，需要不斷地積累和總結。

注：本文作于2009年7月3日20點整
【題目大意】
　　給定一個n*n的棋盤，求放置k個互不攻擊的象的方法數。其中n <= 8，k <= n ^ 2。

【題目分析】
　　對于棋盤放車問題可以用組合數學的知識來解決，但是對于含禁區的擺放問題，雖然組合數學給出了經典的棋盤多項式+容斥原理的解法，但是實際中棋盤多項式的求解是很困難的，因此一般需要借助狀態壓縮動態規劃求解。
　　現在題目中要求出互不攻擊的象的方法數，象的攻擊路線是斜的，是不是可以考慮采用放車的方法來解呢？將棋盤黑白染色，如果一個象在黑色的格子里面，那么它一定不會攻擊到白色的格子，這樣的話可以分開計數，然后最后利用乘法原理加起來就行了。把棋盤旋轉45度，這樣象的攻擊路線就是直的了，如果只考慮一種顏色的話，那么問題就轉變成了經典的放車問題了，可以利用動態規劃解決。
　　設dp[i][j]表示前i行放了j個車的方法數，c[i]表示第i行可以放置的棋子數量，那么轉移方程為：
　　　　dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - (j - 1))
　　需要注意的是c數組應該是增序的，這樣才能保證前面的j-1行放了車，對應這一行就有j-1個位置不可放了。
　　這個題目的dp方程不難想，但是如何把模型轉化到放車問題是不容易想到的，尤其是將棋盤黑白染色后分開計數的想法，非常巧妙。

題目代碼：

注：本文作于2009年6月23日 19點51分