這是《劍指Offer——名企面試官精講典型編程題》一書中的面試題50,此題針對所給條件的不同,將需要截然不同的解題思路和方法。書中給出了針對此題的3種不同條件的解題,本文所要講解的是對其第3種條件的一個改進解法。具體的題目及條件如下。
【題目】:
輸入兩個樹結點,求它們的最低公共祖先。
【補充條件】:
樹是普通的樹,而且樹中的結點沒有指向父節點的指針。
針對上述的題目和條件,書中給出了如下解決方案。
【原方案】:
使用兩個鏈表,對樹進行兩次遍歷以查找兩個樹結點,并保持路徑到兩個鏈表中,從而將問題轉化為求兩個鏈表的最后一個公共結點。
從該方案中,觀察到兩次樹結點查找的遍歷中,其中一個結點的遍歷過的樹結點序列將完全覆蓋查找另一結點時所遍歷的樹結點序列。由此入手,本文提出了如下的改進解決方案。
【改進方案】:
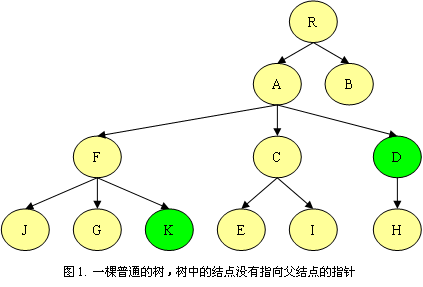
深度優先遍歷樹,并記錄路徑,當找到第一個結點后,在當前基礎上繼續遍歷搜索第二個結點,并記錄第一個結點路徑的變化程度,直到找到第二個結點。最后,根據棧信息和記錄的結點路徑變化程度得到最低公共祖先。如圖1,假設輸入的兩個樹結點為D和K,樹的根節點為R,則求D和K的最低公共結點的過程如下表:
|
步驟 |
棧 |
第一個結點 |
第二個結點 |
路徑變化程度 |
|
1 |
R |
— |
— |
— |
|
2 |
R,A |
— |
— |
— |
|
3 |
R,A,F |
— |
— |
— |
|
4 |
R,A,F,J |
— |
— |
— |
|
5 |
R,A,F,G |
— |
— |
— |
|
6 |
R,A,F,K |
K |
— |
0(或K) |
|
7 |
R,A,C |
K |
— |
1(或A) |
|
8 |
R,A,C,E |
K |
— |
2(或A) |
|
9 |
R,A,C,I |
K |
— |
2(或A) |
|
10 |
R,A,D |
K |
D |
1(或A) |
|
è 得出結果,最低公共祖先結點為A |
從中,可以看到,改進后的方案,只需對樹執行一次遍歷。而在輔助空間的需求上, 只需使用一個棧(外加少量結點指針變量和1個表示路徑變化程度的整型變量)。而且,如果采用遞歸的方式實現,該棧所需保存的信息,還可以通過遞歸時的函數調用棧得以保存。
【附注】:
- 此處,有如下一個問題:
假設待查找公共祖先的兩樹結點,其中一結點在以另一結點為根的子樹上(包括兩結點相同)時,公共祖先的確定規則——
“作為子樹根結點的那個結點”還是“子樹根結點的父節點”?
例如:對上面圖1中的那棵樹,如果待查結點為根結點R和結點F,那么最終的查找結果是為R呢,還是因為R是根結點無父結點而得出NULL?
此問題在書中未提及,但查看書中代碼,確認是選擇了后者;而在本人的樣例代碼中則采用了前面的觀點。 - 在樣例代碼中,對樹結點在棧中的存儲方式略有改動。
- 樣例代碼工程所使用的環境為 Visual C++ 2010;
其中:tree.h/cpp為功能代碼文件,TestLowestCommonAncestor.h/cpp為相應的UT代碼文件;
UT采用gtest所編寫,編譯鏈接請根據gtest在自己本機的路徑狀況修改gtest_link.props文件中相應的鏈接項。