轉(zhuǎn)自:http://apps.hi.baidu.com/share/detail/17558221
既然是解決尋找兩點(diǎn)之間最短路徑的的問題。我們自然會(huì)想一個(gè)描述兩點(diǎn)之間最短路徑特征的命題。
如果在點(diǎn)A和C之間存在一條最短路徑AC,并且在AC上有個(gè)點(diǎn)B,那么,沿這條路徑產(chǎn)生的路徑AB,是點(diǎn)A到點(diǎn)B的最短路徑。
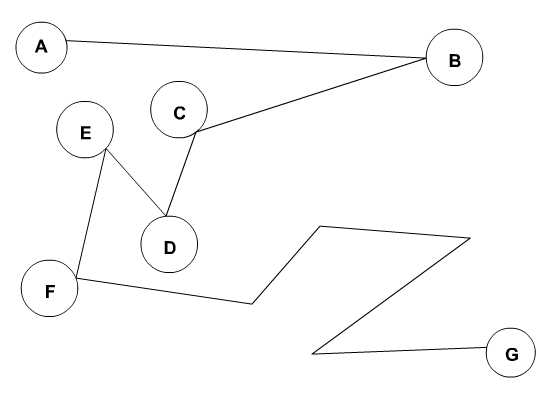
像這張圖,如果這條路徑是A到G的最短路徑,那么AF路徑就一定也是A到F的最短路徑。
用反證法證明的話,可以這么說。如果存在一條更短的A到F的路徑,那么我們完全可以從A走更短的路徑到達(dá)F,然后再?gòu)腇到達(dá)G,那么產(chǎn)生的路徑就比AG要短,這顯然和AG是最短路徑這個(gè)前提矛盾。故AF就一定是最短路徑啦。
同理,我們還能推出,AB,AC,AD,甚至BD,BE都是最短路徑,這個(gè)圖中任意兩點(diǎn)沿這個(gè)路徑所產(chǎn)生的路徑,都是最短路徑。當(dāng)然,這個(gè)最短路徑不是唯一的,這只是其中一條。
利用這個(gè)數(shù)學(xué)原理,我們可以在尋路過程中,率先找到起點(diǎn)到某點(diǎn)的一條最短路徑,那么之后的所有尋路都基于這個(gè)最短路徑之上,而不必考慮起點(diǎn)到這個(gè)點(diǎn)的其他路徑。這樣的方法能剔除大量無謂的路徑,減少時(shí)間和空間的壓力。
那么如何率先找到起點(diǎn)到某點(diǎn)的最短路徑呢?這里用到數(shù)據(jù)結(jié)構(gòu)里面的一種廣度優(yōu)先搜索的方法對(duì)圖進(jìn)行搜索。
廣度優(yōu)先搜索按照從起點(diǎn)到其他點(diǎn)的路徑的長(zhǎng)度,從短到長(zhǎng)一層一層搜索。當(dāng)某個(gè)點(diǎn)第一次被搜索到,那么所搜索的那個(gè)路徑就一定是一條最短路徑了。這個(gè)講起來有點(diǎn)抽象,下面我們用一張3*3的地圖來演示下搜索的過程。
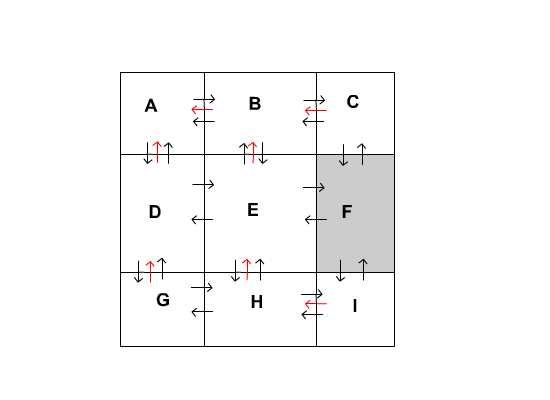
這張地圖中,F(xiàn)為障礙物,A是起點(diǎn),I是終點(diǎn)。每個(gè)格子,即一個(gè)結(jié)點(diǎn),有三部分和搜索有關(guān)的屬性。第一個(gè)是指向和這個(gè)節(jié)點(diǎn)相鄰的結(jié)點(diǎn)的一系列引用(圖中黑色箭頭表示)。第二個(gè)是指向母結(jié)點(diǎn)的引用(圖中紅色箭頭表示),在未開始搜索之前,這個(gè)屬性是空的。第三個(gè)就是一個(gè)布爾值,表示結(jié)點(diǎn)是否是可被搜索的,障礙物默認(rèn)是不可被搜索的,沒有人會(huì)產(chǎn)生一個(gè)經(jīng)過障礙物的路徑吧,所以這個(gè)搜索直接忽略。
將地圖連接好之后,我們會(huì)產(chǎn)生一個(gè)圖(此圖為數(shù)據(jù)結(jié)構(gòu)里面的概念),當(dāng)然,我們也能把這個(gè)圖看成是一個(gè)根節(jié)點(diǎn)是起點(diǎn),元素能重復(fù)的無限深度的樹。
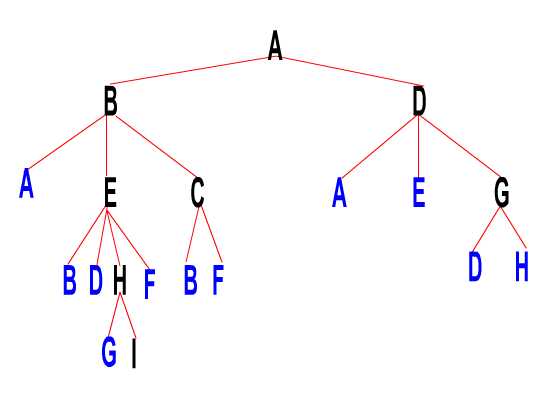
然后我們就開始搜索,首先,從A出發(fā),我們能到B和D,由于B和D是第一次被搜索到,故AB和AD必然是最短路徑(這個(gè)是不爭(zhēng)的事實(shí),他們一步就到了,其他路徑皆是繞圈子)。
恩,很好,那么接下來我們就把B和D的指向母結(jié)點(diǎn)的引用(上面提到的結(jié)點(diǎn)的第二部分屬性,也就是地圖中畫出的紅色箭頭)指向A,表示從起點(diǎn)到達(dá)B和D的最短路徑是從A那過來的,這樣就把路徑儲(chǔ)存下來了。
然后,將B和D設(shè)為不可搜索,表示B和D的最短路徑已經(jīng)產(chǎn)生了,要是下面要是還搜他們,那么產(chǎn)生的路徑一定沒這個(gè)短,因?yàn)樗阉鞯捻樞蚴菑亩痰介L(zhǎng)的嘛。所以就沒有必要對(duì)他們搜索了。
最后,將B和D存入第二層的臨時(shí)數(shù)組,第二輪的搜索就要從B和D開始了!
第二輪,首先,從B開始搜索,像剛才從A開始一樣。我們發(fā)現(xiàn),B的子節(jié)點(diǎn)有三個(gè),其中A被鎖定了(藍(lán)色表示,它的子節(jié)點(diǎn)由于不參與搜索,就暫時(shí)忽略不畫),所以直接忽略A。
然后是E和C,發(fā)現(xiàn)者兩個(gè)沒有被鎖定,那么它們就是第一次出現(xiàn)咯(因?yàn)榈谝淮纬霈F(xiàn)后就要被鎖定,所以沒鎖定的就是第一次出現(xiàn))。恩,把他們像剛才處理B和D一樣,設(shè)置路徑,然后鎖定,再存入第三層的臨時(shí)數(shù)組。
B的子節(jié)點(diǎn)處理完了,然后是D的子節(jié)點(diǎn)。A是鎖定的忽略,E剛才在處理B的子節(jié)點(diǎn)的時(shí)候被鎖了,所以也忽略。恩,G第一次出現(xiàn),把它處理了存入第三層數(shù)組,這樣,第三層就全部處理完了。下面進(jìn)入第三輪搜索。
第三輪中,只有H新來的,其他均是老面孔。H存入第四層數(shù)組,接下來進(jìn)入第四輪搜索。
G是老面孔,I是新來的,而且!I就是我們所要的終點(diǎn)。。OK!,搜索就這樣結(jié)束了!
我們沿著I的指向母結(jié)點(diǎn)的引用,I-H-E-B-A,到達(dá)起點(diǎn),這個(gè)就是我們要找的路徑。
這里,我們不止可以找到起點(diǎn)到終點(diǎn)的最短路徑。在搜索過程中,我們已經(jīng)建立了一個(gè)從起點(diǎn)出發(fā),到任何點(diǎn)的最短路徑的樹。從任何點(diǎn)出發(fā),沿著指向母結(jié)點(diǎn)的引用走到起點(diǎn),都能產(chǎn)生最短路徑。
posted on 2010-11-15 15:54
納蘭伴月 閱讀(693)
評(píng)論(0) 編輯 收藏 引用 所屬分類:
as3