| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 11943 | Accepted: 4112 |
Description
Definition 1 (Spanning Tree): Consider a connected, undirected graph G = (V, E). A spanning tree of G is a subgraph of G, say T = (V', E'), with the following properties:
1. V' = V.
2. T is connected and acyclic.
Definition 2 (Minimum Spanning Tree): Consider an edge-weighted, connected, undirected graph G = (V, E). The minimum spanning tree T = (V, E') of G is the spanning tree that has the smallest total cost. The total cost of T means the sum of the weights on all the edges in E'.
Input
Output
Sample Input
2
3 3
1 2 1
2 3 2
3 1 3
4 4
1 2 2
2 3 2
3 4 2
4 1 2
Sample Output
3
Not Unique!
Source
浠ｇ爜錛?br />
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef struct
{
int x, y, w;
} edge;
edge s[10010];
int top, t[10010];
bool cmp(edge a, edge b)
{
return a.w < b.w;
}
int kru(int n, int m, int x)
{
int i, j, a, b, tag[110], tem, sum, k;
for (i = 0; i < n; ++i)
{
tag[i] = i;
}
k = 1, j = 0, sum = 0;
while (k < n)
{
a = s[j].x - 1;
b = s[j].y - 1;
if (j == x)
{
j++;
continue;
}
if (tag[a] != tag[b])
{
if (x == -1)
{
t[top] = j;
top++;
}
tem = tag[b];
k++, sum += s[j].w;
for (i = 0; i < n; ++i)
{
if (tag[i] == tem)
{
tag[i] = tag[a];
}
}
}
j++;
}
return sum;
}
int main()
{
int p, n, m, cmin;
scanf("%d", &p);
while (p--)
{
int flag = 1;
scanf("%d%d", &n, &m);
for (int i = 0; i < m; ++i)
scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].w);
sort(s, s + m, cmp);
top = 0;
int min = kru(n, m, -1);
int key = top;
for (int l = 0; l < key; ++l)
{
cmin = kru(n, m, t[l]);
if (cmin == min)
{
flag = 0;
printf("Not Unique!\n");
break;
}
}
if (flag)
printf("%d\n", min);
}
return 0;
}
]]>
Sightseeing
Description Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights. Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route. There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday. 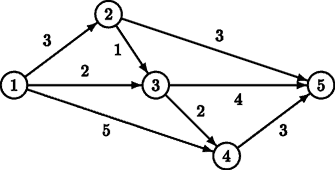 For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7. Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length. Input The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
Output For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 109 = 1,000,000,000. Sample Input 2 5 8 1 2 3 1 3 2 1 4 5 2 3 1 2 5 3 3 4 2 3 5 4 4 5 3 1 5 5 6 2 3 1 3 2 1 3 1 10 4 5 2 5 2 7 5 2 7 4 1 Sample Output 3 2 Hint The first test case above corresponds to the picture in the problem description. Source |
鎬濊礬:渚濇嵁鎻忓啓鍙煡錛屾湰棰樼殑瑕佹眰鍗充究瑕佹眰鍑烘渶鐭礬鍜屾瘮鏈鐭礬闀?鐨勬鐭礬錛屽洜鑰屽彲鐢―ijkstra鏉ュ鐞嗐傜繑瀹炲仛娉曞涓嬶細鐢ㄤ袱緇勬暟紱誨埆鐧昏鏈鐭礬鍜屾鐭礬鐨勯暱搴︼紙dist錛夛紝鏉℃暟錛坈nt錛夛紝鎷滀細絎﹀彿錛坲sed錛夛紝寤轟竴涓紭鍏堥槦鍒楋紝鍏冪礌鍗曚綅鍖呮嫭鑺傜偣搴忓彿錛坴錛夛紝璇ヨ妭鐐硅礬緇忛暱錛坙en錛夛紝浠ュ強鐧昏璺緞縐嶇被錛坮ef錛夛紝姣忔浠庝紭鍏堥槦鍒椾腑鍙栧嚭綆＄敤鑺傜偣鍚庯紝鐢ㄥ畠鎵鐧昏鐨勮礬寰勯暱鏇存柊寰呮瘮鎷熻礬寰勶紝紱誨埆鐢ㄥ畠鍜岀洰鍓嶆墍鐧昏鐨勮鑺傜偣鐨勬渶鐭礬寰勪互鍙婃孌佃礬寰勬瘮鎷燂紝涓剰鏇存柊鏉′歡鍒欑櫥璁拌礬寰勭綾伙紝騫剁敓鎴愭柊鑺傜偣鍔犲叆浼樺厛闃熷垪錛屽悓鏃舵洿鏂扮洰鍓嶈妭鐐瑰璇ョ綾昏礬寰勬潯鏁般備竾涓涓嶄腑鎰忔潯浠剁劧鑰屼腑鎰忔販鍚岃仈緋伙紝鍒欏鍔犵浉搴旂殑鏉℃暟鍒拌鑺傜偣鎵鐧昏鐨勮礬寰勬潯鏁頒笂銆?/span>
浠ｇ爜錛?br />
#include <memory.h>
#include <queue>
#define N 1001
#define M 10001
#define INF 0x7fffffff
#define clr(a) memset(a, 0, sizeof(a))
using namespace std;
struct Edge
{
int v, len, ref;
Edge *link;
Edge new_E(int v1, int l, int r)
{
v = v1, len = l, ref = r;
return *this;
}
} *E[N], mempool[M];
int dist[N][2], used[N][2], cnt[N][2];
int n, m, memh, S, T;
void AddEdge(int u, int v, int len)
{
Edge *e = &mempool[memh++];
e -> v = v;
e -> len = len;
e -> link = E[u];
E[u] = e;
}
bool operator < (Edge a, Edge b)
{
return a.len > b.len;
}
priority_queue <Edge, vector <Edge> > Q;
void InitData()
{
int i, u, v, len;
memh = 0;
scanf("%d%d", &n, &m);
clr(E);
for (i = 1; i <= m; ++i)
{
scanf("%d%d%d", &u, &v, &len);
AddEdge(u, v, len);
}
scanf("%d%d", &S, &T);
}
int Dijstra()
{
Edge D, P;
clr(cnt);
clr(used);
for (int i = 1; i <= n; ++i)
dist[i][0] = dist[i][1] = INF;
dist[S][0] = 0;
cnt[S][0] = 1;
while (!Q.empty())
Q.pop();
Q.push(D.new_E(S, 0, 0));
while (!Q.empty())
{
P = Q.top();
Q.pop();
if (!used[P.v][P.ref])
{
used[P.v][P.ref] = 1;
for (Edge *e = E[P.v]; e; e = e -> link)
{
int tmp = P.len + e -> len;
if (tmp < dist[e -> v][0])
{
if (dist[e -> v][0] != INF)
{
dist[e -> v][1] = dist[e -> v][0];
cnt[e -> v][1] = cnt[e -> v][0];
Q.push(D.new_E(e -> v, dist[e -> v][0], 1));
}
dist[e -> v][0] = tmp;
cnt[e -> v][0] = cnt[P.v][P.ref];
Q.push(D.new_E(e -> v, tmp, 0));
}
else
if (tmp == dist[e -> v][0])
{
cnt[e -> v][0] += cnt[P.v][P.ref];
}
else
if (tmp < dist[e -> v][1])
{
dist[e -> v][1] = tmp;
cnt[e -> v][1] = cnt[P.v][P.ref];
Q.push(D.new_E(e -> v, tmp, 1));
}
else
if (dist[e -> v][1] == tmp)
{
cnt[e -> v][1] += cnt[P.v][P.ref];
}
}
}
}
if (dist[T][1] - 1 == dist[T][0])
cnt[T][0] += cnt[T][1];
return cnt[T][0];
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
InitData();
printf("%d\n", Dijstra());
}
}
]]>
Slim Span
Description Given an undirected weighted graph G, you should find one of spanning trees specified as follows. The graph G is an ordered pair (V, E), where V is a set of vertices {v1, v2, …, vn} and E is a set of undirected edges {e1, e2, …, em}. Each edge e ∈ E has its weight w(e). A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T. 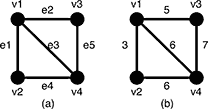 Figure 5: A graph G and the weights of the edges For example, a graph G in Figure 5(a) has four vertices {v1, v2, v3, v4} and five undirected edges {e1, e2, e3, e4, e5}. The weights of the edges are w(e1) = 3, w(e2) = 5, w(e3) = 6, w(e4) = 6, w(e5) = 7 as shown in Figure 5(b). 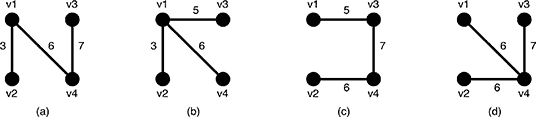 Figure 6: Examples of the spanning trees of G There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree Ta in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree Ta is 4. The slimnesses of spanning trees Tb, Tc and Td shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1. Your job is to write a program that computes the smallest slimness. Input The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.
Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. ak and bk (k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices vak and vbk connected by the kth edge ek. wk is a positive integer less than or equal to 10000, which indicates the weight of ek. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices). Output For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters. Sample Input 4 5 1 2 3 1 3 5 1 4 6 2 4 6 3 4 7 4 6 1 2 10 1 3 100 1 4 90 2 3 20 2 4 80 3 4 40 2 1 1 2 1 3 0 3 1 1 2 1 3 3 1 2 2 2 3 5 1 3 6 5 10 1 2 110 1 3 120 1 4 130 1 5 120 2 3 110 2 4 120 2 5 130 3 4 120 3 5 110 4 5 120 5 10 1 2 9384 1 3 887 1 4 2778 1 5 6916 2 3 7794 2 4 8336 2 5 5387 3 4 493 3 5 6650 4 5 1422 5 8 1 2 1 2 3 100 3 4 100 4 5 100 1 5 50 2 5 50 3 5 50 4 1 150 0 0 Sample Output 1 20 0 -1 -1 1 0 1686 50 Source |
棰樼洰灝辨槸鐢熸垚涓媯墊爲錛岃姹傝竟鏉冩渶澶у噺鏈灝忕殑宸渶灝忋?br />鏍規嵁Kruskal鎬濇兂錛屾妸杈規帓搴忥紝涔嬪悗鏋氫婦涓涓嬪氨琛屼簡銆?br />
浠ｇ爜錛?br />
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 5005;
const int INF = 1 << 29;
struct edge
{
int st, ed, w;
bool operator < (edge a) const
{
return w < a.w;
}
} e[M];
int n, m, ans, num, temp;
int f[105], rank[105];
void makeset()
{
for (int i = 1; i <= n; ++i)
f[i] = i;
memset(rank, 0, sizeof(rank));
}
int find(int x)
{
while (f[x] != x) x = f[x];
return x;
}
void unionset(int a, int b)
{
int p = find(a);
int q = find(b);
if (rank[p] > rank[q])
f[q] = p;
else
if (rank[p] < rank[q])
f[p] = q;
else
{
f[p] = q;
rank[q]++;
}
}
void kruskal()
{
ans = INF;
for (int i = 0; i < m - n + 2; ++i)
{
makeset();
temp = -1;
num = 0;
for (int j = i; j < m; ++j)
{
if (find(e[j].st) != find(e[j].ed))
{
num++;
unionset(e[j].st, e[j].ed);
if (num == n - 1)
{
temp = e[j].w - e[i].w;
break;
}
}
}
if (temp == -1) break;
if (temp != -1 && temp < ans) ans = temp;
}
if (ans >= INF) printf("-1\n");
else printf("%d\n", ans);
}
int main()
{
while (scanf("%d%d", &n, &m), n || m)
{
for (int i = 0; i < m; ++i)
scanf("%d%d%d", &e[i].st, &e[i].ed, &e[i].w);
sort(e, e + m);
kruskal();
}
return 0;
}
]]>
Remmarguts' Date
Description "Good man never makes girls wait or breaks an appointment!" said the mandarin duck father. Softly touching his little ducks' head, he told them a story. "Prince Remmarguts lives in his kingdom UDF – United Delta of Freedom. One day their neighboring country sent them Princess Uyuw on a diplomatic mission." "Erenow, the princess sent Remmarguts a letter, informing him that she would come to the hall and hold commercial talks with UDF if and only if the prince go and meet her via the K-th shortest path. (in fact, Uyuw does not want to come at all)" Being interested in the trade development and such a lovely girl, Prince Remmarguts really became enamored. He needs you - the prime minister's help! DETAILS: UDF's capital consists of N stations. The hall is numbered S, while the station numbered T denotes prince' current place. M muddy directed sideways connect some of the stations. Remmarguts' path to welcome the princess might include the same station twice or more than twice, even it is the station with number S or T. Different paths with same length will be considered disparate. Input The first line contains two integer numbers N and M (1 <= N <= 1000, 0 <= M <= 100000). Stations are numbered from 1 to N. Each of the following M lines contains three integer numbers A, B and T (1 <= A, B <= N, 1 <= T <= 100). It shows that there is a directed sideway from A-th station to B-th station with time T. The last line consists of three integer numbers S, T and K (1 <= S, T <= N, 1 <= K <= 1000). Output A single line consisting of a single integer number: the length (time required) to welcome Princess Uyuw using the K-th shortest path. If K-th shortest path does not exist, you should output "-1" (without quotes) instead. Sample Input 2 2 1 2 5 2 1 4 1 2 2 Sample Output 14 Source POJ Monthly,Zeyuan Zhu |
絎琄鐭礬闂錛屽ぇ姒傛剰鎬濆氨鏄粰浣燦涓偣錛孧鏉¤竟錛岃竟鏄湁鍚戠殑錛岀粰浣犳瘡鏉¤竟鐨勮竟鏉冿紝緇欎綘涓涓猄璧峰鐐癸紝T緇撴潫鐐癸紝鍜屼竴涓狵錛屾眰S鍒癟鐨勭K鐭礬銆?br />SPFA+A*鍚彂寮忔悳绱€?br />
璇磋鍚彂寮忔悳绱㈠惂錛?br />
閫氬父鍦ㄨВ鍐抽棶棰樼殑鏃跺欙紝鎴戜滑闇瑕佺敤鍒版悳绱㈢畻娉曪紝鐢卞凡鐭ョ姸鎬佹帹鍑烘柊鐨勭姸鎬侊紝鐒跺悗媯楠屾柊鐨勭姸鎬佹槸涓嶆槸灝辨槸鎴戜滑瑕佹眰鐨勬渶浼樿В銆傛楠屽畬鎵鏈夌殑鐘舵佸疄闄呬笂灝辯浉褰撲簬閬嶅巻浜嗕竴寮犻殣寮忓浘銆傞仐鎲劇殑鏄紝鎵鏈夌殑鐘舵佺粍鎴愮殑鐘舵佺┖闂村線寰鏄垚鎸囨暟綰у埆澧為暱鐨勶紝涔熷氨閫犳垚浜嗛亶鍘嗛渶瑕佺敤鍒版寚鏁扮駭鍒殑鏃墮棿錛屽洜姝わ紝綰補鐨勬毚鍔涙悳绱紝鏃剁┖鏁堢巼閮芥瘮杈冧綆銆傚綋鐒訛紝鎴戜滑鍦ㄧ敓媧諱腑閬囧埌浜嗙被浼間簬鎼滅儲鐨勯棶棰橈紝鎴戜滑騫朵笉浼氱洸鐩湴鍘繪悳瀵繪瘡涓縐嶇姸鎬侊紝鎴戜滑浼氶氳繃鎴戜滑鐨勬濈淮錛岄夋嫨涓鏉℃渶鎺ヨ繎浜庣洰鏍囩殑璺緞鎴栬呮槸榪戜技浜庢渶鐭殑璺緞鍘誨畬鎴愭悳绱換鍔°傚綋鎴戜滑鎯寵璁＄畻鏈哄幓瀹屾垚榪欐牱涓欏規悳绱換鍔＄殑鏃跺欙紝灝卞緱璁╄綆楁満鍍忎漢涓鏍瘋兘澶熷尯鍒嗗敖閲忕煭鐨勮礬寰勶紝浠ヤ究楂樻晥鍦版壘鍒版渶浼樿В銆傝繖鏃跺彲浠ユ妸璁＄畻鏈虹湅浣滄槸涓縐嶆櫤鑳戒綋(agent)鍙互瀹炵幇鐢卞垵濮嬬姸鎬佸悜鐩爣鐘舵佺殑杞Щ銆?/span>
鏈変竴縐嶈椽蹇冪瓥鐣ワ紝鍗蟲瘡涓姝ヨ漿縐婚兘鐢辮綆楁満閫夋嫨褰撳墠鐨勬渶浼樿В鐢熸垚鏂扮殑鐘舵侊紝涓鐩村埌杈劇洰鏍囩姸鎬佷負姝€傝繖鏍峰仛鐨勬椂闂存晥鐜囪櫧鐒惰緝楂橈紝浣嗘槸璐績鐨勭瓥鐣ュ彧鏄敤鍒頒簡灞閮ㄧ殑鏈浼樿В錛屽茍涓嶈兘淇濊瘉鏈鍚庡埌杈劇洰鏍囩姸鎬佸緱鍒扮殑鏄叏灞鏈浼樿В銆傚湪鑳戒繚璇佸叏灞鏈浼樿В鐨勮寖鍥村唴錛岃椽蹇冪畻娉曡繕鏄緢鏈夌敤鐨勩傛瘮濡傝鎴戜滑鐔熺煡鐨?/span>Dijkstra綆楁硶姹傚崟婧愭渶鐭礬銆傛瘡嬈￠夋嫨璺濈婧愯妭鐐規渶鐭窛紱葷殑寰呮墿灞曡妭鐐硅繘琛屾墿灞曪紝鏈鍚庡氨鑳界敓鎴愭簮鑺傜偣鍒版墍鏈夎妭鐐圭殑鏈鐭礬寰勩備笅闈細璁插埌Dijkstra鐨勬墿灞曪紝褰撶悊瑙ｄ簡榪欎釜綆楁硶涔嬪悗錛屾垜鎯籌紝浣犱細瀵?/span>Dijkstra鏈夋洿娣卞叆鐨勭悊瑙ｃ?/span>
榪欏氨鏄?/span>A*綆楁硶銆傚畾涔夊垵濮嬬姸鎬?/span>S錛岀洰鏍囩姸鎬?/span>t錛?/span>g(s)鏄敱鍒濆鐘舵佽漿縐誨埌褰撳墠鐘舵?/span>s鎵緇忚繃鐨勮礬寰勯暱搴︼紝h*(s)鏄綋鍓嶇姸鎬?/span>s璺濈鐩爣鐘舵?/span>t鐨勫疄闄呴暱搴︼紝浣嗘槸涓鑸儏鍐典笅鎴戜滑鏄笉鐭ラ亾h*(s)鐨勫肩殑錛屾墍浠ヨ繕瑕佸畾涔変竴涓及浠峰嚱鏁?/span>h(s)錛屾槸瀵?/span>h*(s)鍑芥暟鍊肩殑涓嬬晫鐨勪及璁★紝涔熷氨鏄湁h(s)<=h*(s)錛岃繖鏍烽渶瑕佷竴涓潯浠訛紝浣垮緱鐢?/span>s1鐢熸垚鐨勬瘡鐘舵?/span>s2錛岄兘鏈?/span>h(s1)<=h(s2)錛岃繖鏄竴涓浉瀹圭殑浼頒環鍑芥暟銆傚啀瀹氫箟f(s)=g(s)+h(s)涓哄惎鍙戝嚱鏁幫紝鍥犱負h(s)鏄崟璋冮掑鐨勶紝鎵浠?/span>f(s)涔熸槸鍗曡皟閫掑鐨勩傝繖鏍?/span>f(s)灝變及璁″嚭浜嗙敱鍒濆鐘舵佺殑鎬諱綋浠ｄ環銆?/span>A*綆楁硶灝遍氳繃鏋勯犺繖鏍蜂竴涓惎鍙戝嚱鏁幫紝灝嗘墍鏈夌殑寰呮墿灞曠姸鎬佸姞鍏ュ埌闃熷垪閲岋紝姣忔浠庨槦鍒楅噷閫夋嫨f(s)鍊兼渶灝忕殑鐘舵佽繘琛屾墿灞曘傜敱浜庡惎鍙戝嚱鏁扮殑浣滅敤錛屼嬌寰楄綆楁満鍦ㄨ繘琛岀姸鎬佽漿縐葷殑鏃跺欏敖閲忛伩寮浜嗕笉鍙兘浜х敓鏈浼樿В鐨勫垎鏀紝鑰岄夋嫨鐩稿杈冩帴榪戞渶浼樿В鐨勮礬寰勮繘琛屾悳绱紝鎻愰珮浜嗘悳绱㈡晥鐜囥?/span>
璁插埌榪欓噷錛屽彲鑳藉凡緇忓A*綆楁硶鐨勬蹇墊湁鐐圭湁鐩簡銆備笅闈㈡垜鍐嶆潵鍋氫竴涓瘮杈冿紝灝辯敤涓婇潰璁插埌鐨?/span>Dijkstra鐨勪緥瀛愩?/span>Dijkstra綆楁硶璇寸殑鏄瘡嬈￠夋嫨璺濈婧愮偣鏈鐭窛紱葷殑鐐硅繘琛屾墿灞曘傚綋鐒跺彲浠ョ湅鍋氫簨鍏堝皢婧愮偣鍒版墍鏈夎妭鐐硅窛紱葷殑鍊間繚瀛樺湪涓涓紭鍏堥槦鍒楅噷錛屾瘡嬈′粠浼樺厛闃熷垪閲屽嚭闃熸渶鐭窛紱葷殑鐐規墿灞曪紝姣忎釜鐐圭殑鎵╁睍娑夊強鍒拌鏇存柊闃熷垪閲屾墍鏈夊緟鎵╁睍鑺傜偣鐨勮窛紱誨鹼紝姣忎釜鑺傜偣鍙兘榪涢槦涓嬈★紝灝遍渶瑕佹湁涓涓〃鏉ヨ褰曟瘡涓妭鐐圭殑鍏ラ槦嬈℃暟錛堝氨鏄畻娉曚腑鐢ㄥ埌鐨勬爣璁版暟緇勶級銆傚皢Dijkstra姹傛渶鐭礬鐨勬柟娉曟墿灞曪紝榪欓亾棰樼洰瑕佹眰鐨勬槸涓ょ偣闂寸k鐭礬銆傜被姣斾簬Dijkstra綆楁硶鍙互棣栧厛紜畾涓嬮潰鍑犱釜鎼滅儲絳栫暐錛?/span>
1銆?/span>鐢ㄤ紭鍏堥槦鍒椾繚瀛樿妭鐐硅繘琛屾悳绱€?/span>
2銆?/span>鏀懼紑姣忎釜鑺傜偣鐨勫叆闃熸鏁幫紝姹?/span>k鐭礬錛屾瘡涓妭鐐瑰彲浠ュ叆闃?/span>k嬈°?/span>
棣栧厛鐪嬬涓涓瓥鐣ワ紝鍦?/span>A*綆楁硶涓敤浼樺厛闃熷垪灝辨槸瑕佺敤鍒板惎鍙戝嚱鏁?/span>f(s)紜畾鐘舵佸湪浼樺厛闃熷垪閲岄潰鐨勪紭鍏堢駭銆傚叾瀹?/span>Dijkstra鐢ㄥ埌鐨勪紭鍏堥槦鍒楀疄闄呬笂灝辨槸浼頒環鍑芥暟鍊間負0錛屽惎鍙戝嚱鏁?/span>f(s)=g(s)錛屽嵆鏄夊彇鍒版簮鐐硅窛紱繪渶榪戠殑鐐硅繘琛屾墿灞曘傚洜涓?/span>h(s)=0婊¤凍浜嗕及浠峰嚱鏁扮浉瀹硅繖涓潯浠躲傝繖棰樻眰k鐭礬灝變笉鑳藉崟綰殑浣跨敤h(s)=0榪欎釜浼頒環鍑芥暟銆傝В鍐寵繖閬撻鐨勬椂鍊欓夊彇h(x)=dt(x), dt(x)鏄?/span>x鑺傜偣鍒扮洰鏍囪妭鐐圭殑鏈鐭窛紱匯傛渶鐭窛紱誨彲浠ュ紑濮嬬敱Dijkstra鐩存帴姹傚緱銆?/span>
鍐嶇湅絎簩涓瓥鐣ワ紝鎺у埗姣忎釜鑺傜偣鐨勫叆闃燂紙鎴栧嚭闃燂級嬈℃暟涓?/span>k嬈★紝鍙互鎵懼埌絎?/span>k鐭礬寰勩傚彲鑳借繖鏍鋒兂鏈夌偣涓昏鐨勫鐢紝閭ｄ箞鎴戝氨鍏堟潵璇佹槑榪欐牱涓涓粨璁猴細
濡傛灉x鏄?/span>s鍒?/span>t鐨勭k鐭礬寰勪笂鐨勪竴涓妭鐐癸紝閭ｄ箞鐢辮繖鏉¤礬寰?/span>s鍒?/span>x鏄?/span>s鍒?/span>x鐨勭m鐭礬寰勶紝鍒欎笉鍙兘鏈?/span>m>k銆傜敤鍙嶈瘉娉曞緢瀹規槗寰楀嚭錛氬鏋滆繖鏉¤礬寰勬槸s鍒?/span>x鐨勭m鐭礬寰勶紝濡傛灉m>k錛岄偅涔堢粡榪?/span>x鍒?/span>t鐨勮礬寰勫氨鏈?/span>m-1鏉℃瘮褰撳墠璺緞瑕佺煭錛屼笉絎﹀悎褰撳墠璺緞鏄?/span>s鍒?/span>t鐨勭k鐭礬寰勩?br />
#include <algorithm>
#include <queue>
#include <vector>
#include <cstring>
#define MAXN 10005 //杈規暟
#define inf 1 << 25
using namespace std;
int dis[MAXN];
struct node
{
int v, dis;
};
struct edge
{
int v, w;
friend bool operator < (edge a, edge b)
{
return (a.w + dis[a.v]) > (b.w + dis[b.v]);
}
};
vector <node> map[MAXN];
vector <node> remap[MAXN];
int n, m; //n鏄妭鐐規暟錛宮鏄竟鏁般?/span>
int s, t, k; //s鏄搗濮嬬偣錛宼鏄粨鏉熺偣錛宬鏄k灝忋?/span>
void init()
{
int i;
for (i = 0; i < MAXN; ++i)
map[i].clear();
for (i = 0; i < MAXN; ++i)
remap[i].clear();
}
void spfa(int s)
{
int i;
bool used[MAXN];
memset(used, 0, sizeof(used));
for (i = 0; i < MAXN; ++i)
dis[i] = inf;
dis[s] = 0;
used[s] = true;
queue <int> q;
q.push(s);
while (!q.empty())
{
int u = q.front();
q.pop();
used[u] = false;
for (i = 0; i < remap[u].size(); ++i)
{
node p = remap[u][i];
if (dis[p.v] > dis[u] + p.dis)
{
dis[p.v] = dis[u] + p.dis;
if (!used[p.v])
{
used[p.v] = true;
q.push(p.v);
}
}
}
}
}
int a_star()
{
if (s == t)
k++; //娉ㄦ剰錛岃搗濮嬪拰緇撴潫涓鏍鳳紝k瑕?1錛?/span>
if (dis[s] == inf)
return -1;
int i, x, len, cnt[MAXN];
edge n1, n2;
priority_queue <edge> q;
memset(cnt, 0, sizeof(cnt));
n1.v = s;
n1.w = 0;
q.push(n1);
while (!q.empty())
{
n2 = q.top();
q.pop();
x = n2.v;
len = n2.w;
cnt[x]++;
if (cnt[t] == k)
return len;
if (cnt[x] > k)
continue;
for (i = 0; i < map[n2.v].size(); ++i)
{
n1.v = map[n2.v][i].v;
n1.w = len + map[n2.v][i].dis;
q.push(n1);
}
}
return -1;
}
int main()
{
int i;
node p;
while (scanf("%d%d", &n, &m) != EOF)
{
init();
int a, b, l;
for (i = 1; i <= m; ++i)
{
scanf("%d%d%d", &a, &b, &l);
p.v = b;
p.dis = l;
map[a].push_back(p);
p.v = a;
remap[b].push_back(p);
}
scanf("%d%d%d", &s, &t, &k);
spfa(t);
int ans = a_star();
printf("%d\n", ans);
}
return 0;
}
]]>